歴史的功績の解説– category –
-

永遠に到達できない?ゼノンの二分法のパラドックスを徹底解説!
ゼノンの二分法のパラドックスを解説し、その歴史的背景と現代数学における解決法を探ります。古代ギリシャ哲学者ゼノンによって提起されたこのパラドックスは、目的地に到達する前に無限の中間点を通過しなければならないという理由で、移動が不可能であると主張します。記事では、この直感に反する主張がどのように現代数学によって克服されているか、無限等比級数の概念を通じて説明しています。 -

アキレスと亀のパラドックスをわかりやすく解説!論破の鍵は収束する無限!
パラドックスの中で有名な「アキレスと亀」。足の速いアキレスが足の遅い亀に追いつくのは当然のように思えますが、古代ギリシャの哲学者ゼノンの考え方によれば追いつけなくなってしまいます。この記事では、ゼノンの考え方を図入りで説明しながら、パラドックスを解決する方法を紹介します。紀元前に無限の考え方を扱うのは難しかったようです。 -

三平方の定理の証明⑯~2023年最新!三角比を用いた証明をわかりやすく解説! 発見者は10代の少女?~
この記事では、数ある三平方の定理の証明の中でも、2023年最新の証明方法を紹介します。循環論法になりやすい三角比を使った珍しい証明方法です。話題になっている方法をどこよりもていねいに解説しています。 -

【証明あり】単位分数分解のやり方を解説!単位分数の和は無限通りに表せる!
分数を単位分数の和で表す「単位分数分解」。実は、単位分数分解は機械的かつ無限通りに行うことができます。この記事では、分解の方法を2種類解説するだけでなく、どんな分数でも無限通りに単位分数分解できる理由をしっかりと証明。例をたくさん使っているため、理解しやすい記事となっています。 -

ヒポクラテスの三日月~定理の内容や証明をわかりやすく解説!応用例も紹介!~
中学受験で登場する「ヒポクラテスの定理」。この定理は今から約2500年前に生まれ、曲線図形の面積が直線図形の面積と等しくなるという観点から、当時のギリシャに大きな衝撃を与えました。この記事では、その歴史について触れながらも定理の内容やその証明、応用例について解説します。 -

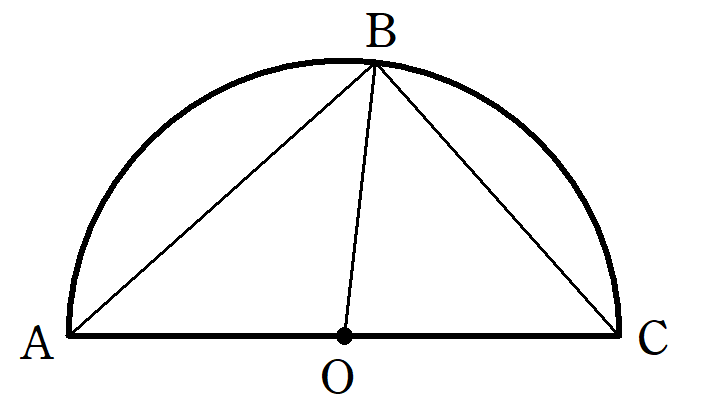
タレスの定理~中学3年生で習う円の定理を解説!証明は超簡単!~
世界で最初に証明された定理は「タレスの定理」であり、「半円に内接する三角形は直角三角形である」という内容です。実は、タレスの定理と呼ばれる定理は他にもあり、すべて現在の中学レベルの内容でした。それらの紹介と共に、タレスの定理が後世の数学にどのような影響を与えたのかを解説します。
1