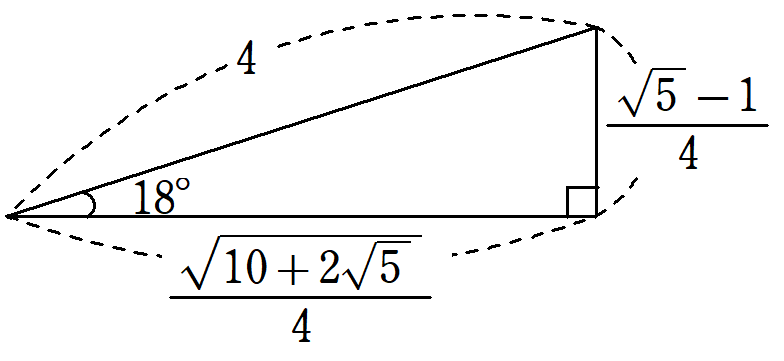教科書数学– category –
-

三平方の定理の証明を16種類紹介! 由来や歴史、対象学年まで掲載
100種類以上あると言われる三平方の定理の証明の中から有名なものを抜粋。さらに、必要な予備知識の対象学年で、証明を分類。証明の複雑さや美しさも、主観で5段階評価しました。この記事を読むことで、自分に合った三平方の定理の証明方法が見つけられます。 -

三平方の定理の証明⑭⑮~教科書に載っている証明方法をわかりやすく解説! 実はインドのバスカラの証明だった?~
この記事では、数ある三平方の定理の証明の中でも、中3の教科書によく出てくる2つの証明方法を紹介します。4つの直角三角形を組み合わせてできる図形、誰もが見たことあるはず!? しかも、そのうちの1つはインドの大数学者バスカラに縁があるものです。その歴史と証明を現役数学教員が解説します。 -

三平方の定理の証明⑬~外接円と直角二等辺三角形を利用した証明をわかりやすく解説!~
三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。 この記事では、外接円と直角二等辺三角形を利用した証明方法を、現役数学教員が... -

収束判定法:ダランベールからコーシーの証明
級数が収束するかどうかを判定するための方法として、「ダランベールの収束判定法」と「コーシーの収束判定法」があります。この2つの収束判定法の関係について考えま... -

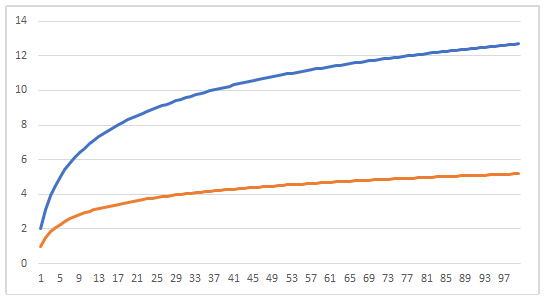
コーシーの収束判定法
級数が収束するかどうかを計算から判定することができる方法です。いくつかの例はもちろん、なぜこの方法で判定できるのかを証明してみましょう。 【Ⅰ コーシーの収束... -

ダランベールの収束判定法
級数が収束するかどうかを計算から判定することができる方法です。いくつかの例はもちろん、なぜこの方法で判定できるのかを証明してみましょう。 【Ⅰ ダランベールの... -

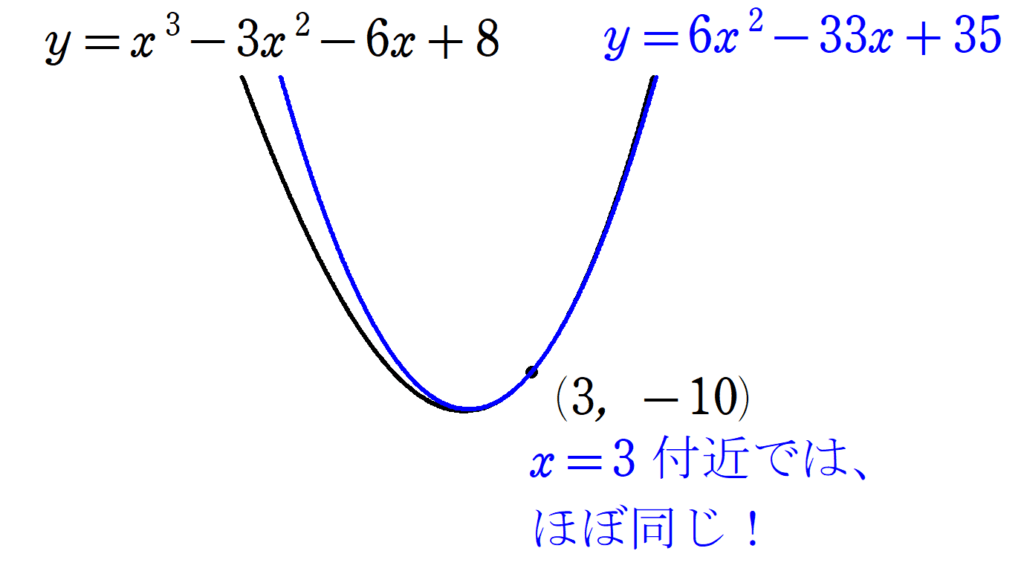
テイラーの定理~具体例からわかりやすく解説! 剰余項の由来はコーシーの平均値の定理!?~
解析学で非常に重要な「テイラー級数」。その基になっているのが「テイラーの定理」です。剰余項を含め、定理の内容を具体例からわかりやすく解説し、証明へと進みます。 -

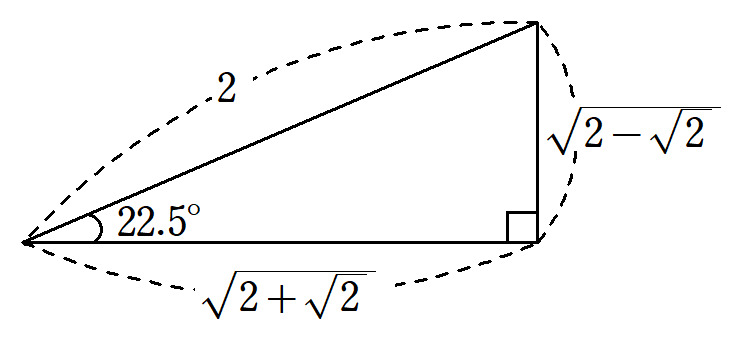
22.5°の三角比 ~半角の公式を使わずに、sin22.5°, cos22.5°, tan22.5°を求める方法を解説!~
22.5°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が2通りの方法で解説。この記事を読むことで、数学Ⅱの半角の公式を使わずに、数学Ⅰまでの知識で値を求める方法がわかります。 -

18°の三角比 ~黄金三角形からsin18°, cos18°, tan18°の値の求める方法を解説~
18°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。この記事を読むことで、36°の三角比から半角の公式を用いる方法、黄金三角形から直接cos18°を求める方法の2種類について理解することができます。 -

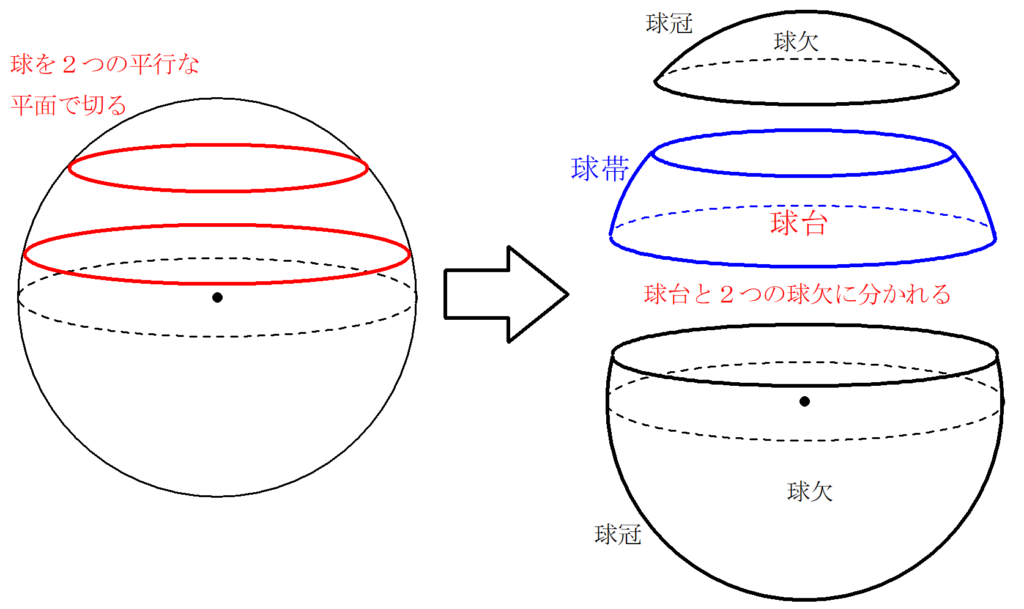
球台と球帯
球を2つの平面で切り取ってできた球台について考えます。 Ⅰ 球台と球帯とは? Ⅱ 球台の体積 Ⅲ 球帯の面積 【Ⅰ 球台と球帯とは?】 前記事の「球欠と球冠」同様...