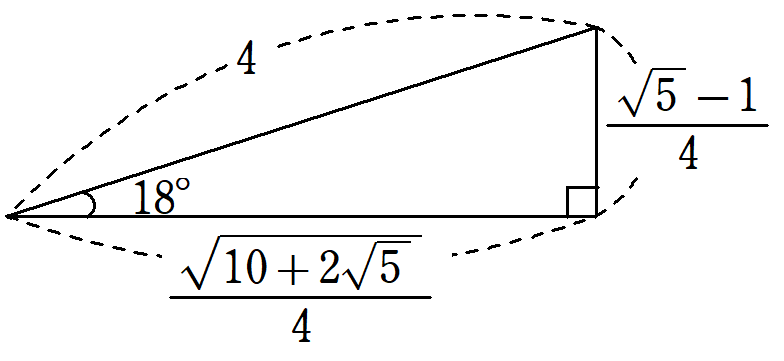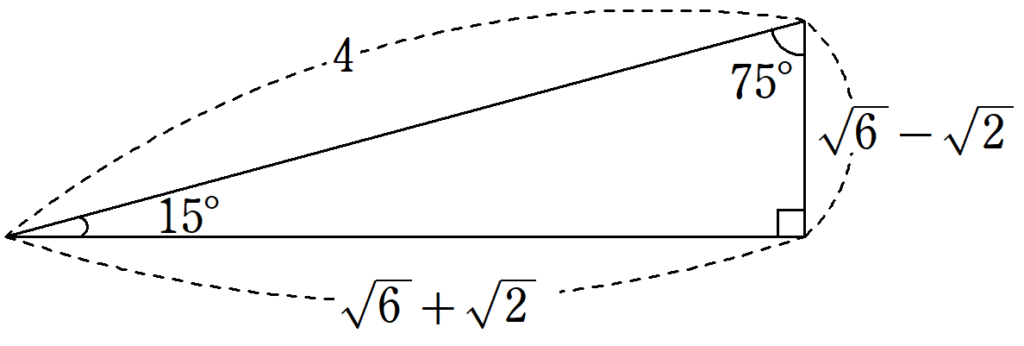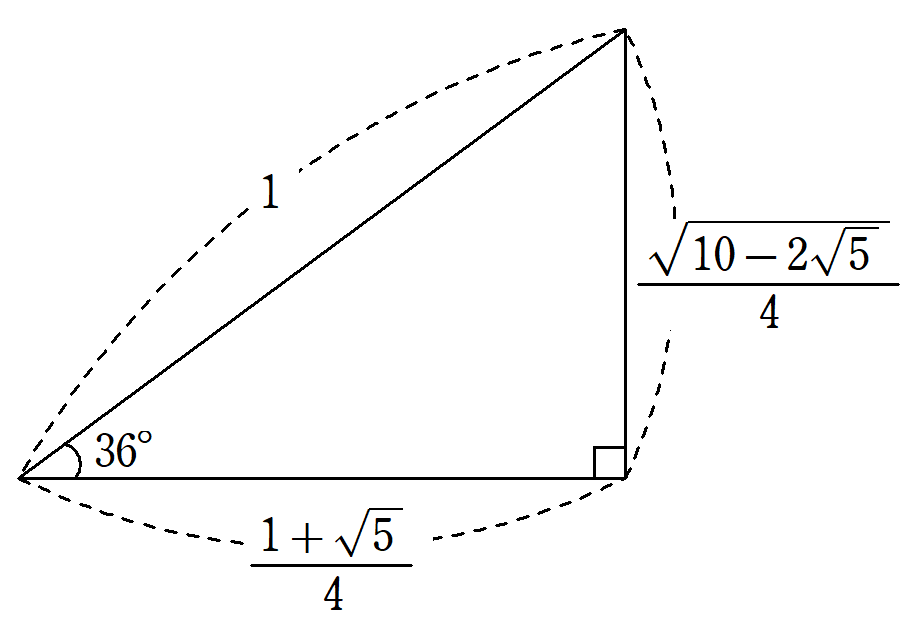高校数学– category –
-

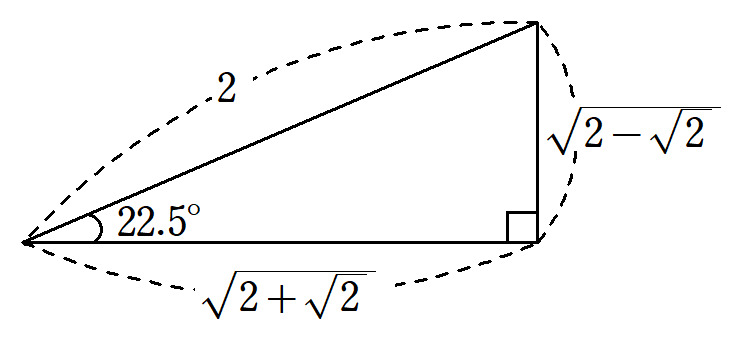
22.5°の三角比 ~半角の公式を使わずに、sin22.5°, cos22.5°, tan22.5°を求める方法を解説!~
22.5°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が2通りの方法で解説。この記事を読むことで、数学Ⅱの半角の公式を使わずに、数学Ⅰまでの知識で値を求める方法がわかります。 -

18°の三角比 ~黄金三角形からsin18°, cos18°, tan18°の値の求める方法を解説~
18°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。この記事を読むことで、36°の三角比から半角の公式を用いる方法、黄金三角形から直接cos18°を求める方法の2種類について理解することができます。 -

15°の三角比~sin15°, cos15°, tan15°の値の求め方を3種類解説! 加法定理、半角の公式、直角三角形で導ける!~
15°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。この記事を読むことで、三角関数の加法定理や半角の公式を使う方法だけでなく、幾何的に求める方法まで理解することができます。 -

36°の三角比 ~黄金比からsin36°, cos36°, tan36°の値を求める方法を解説!~
36°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。値を求める鍵は、古来から人間を魅了してきた黄金比です。この記事を読むことで、黄金比の計算が36°の三角比にとう繋がっているかがわかります。 -

【有名問題】√2が無理数であることの証明~3種類の証明方法とは?~
古代ギリシャから考えられていたルート2 が無理数であることの証明。その歴史の深さと、実際の証明方法を3種類解説します。
1