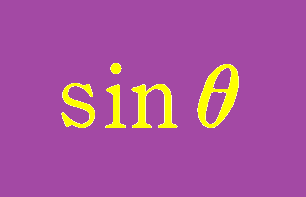大学・一般数学– category –
-

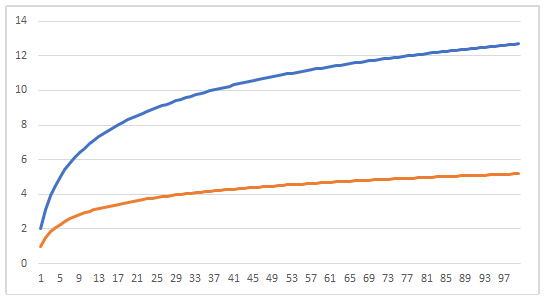
収束判定法:ダランベールからコーシーの証明
級数が収束するかどうかを判定するための方法として、「ダランベールの収束判定法」と「コーシーの収束判定法」があります。この2つの収束判定法の関係について考えま... -

コーシーの収束判定法
級数が収束するかどうかを計算から判定することができる方法です。いくつかの例はもちろん、なぜこの方法で判定できるのかを証明してみましょう。 【Ⅰ コーシーの収束... -

ダランベールの収束判定法
級数が収束するかどうかを計算から判定することができる方法です。いくつかの例はもちろん、なぜこの方法で判定できるのかを証明してみましょう。 【Ⅰ ダランベールの... -

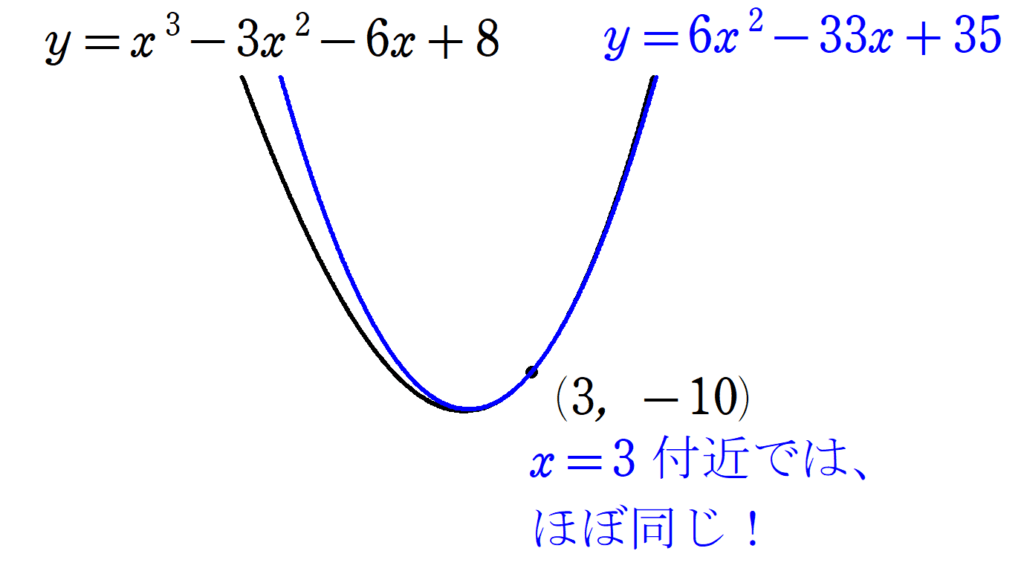
テイラーの定理~具体例からわかりやすく解説! 剰余項の由来はコーシーの平均値の定理!?~
解析学で非常に重要な「テイラー級数」。その基になっているのが「テイラーの定理」です。剰余項を含め、定理の内容を具体例からわかりやすく解説し、証明へと進みます。 -

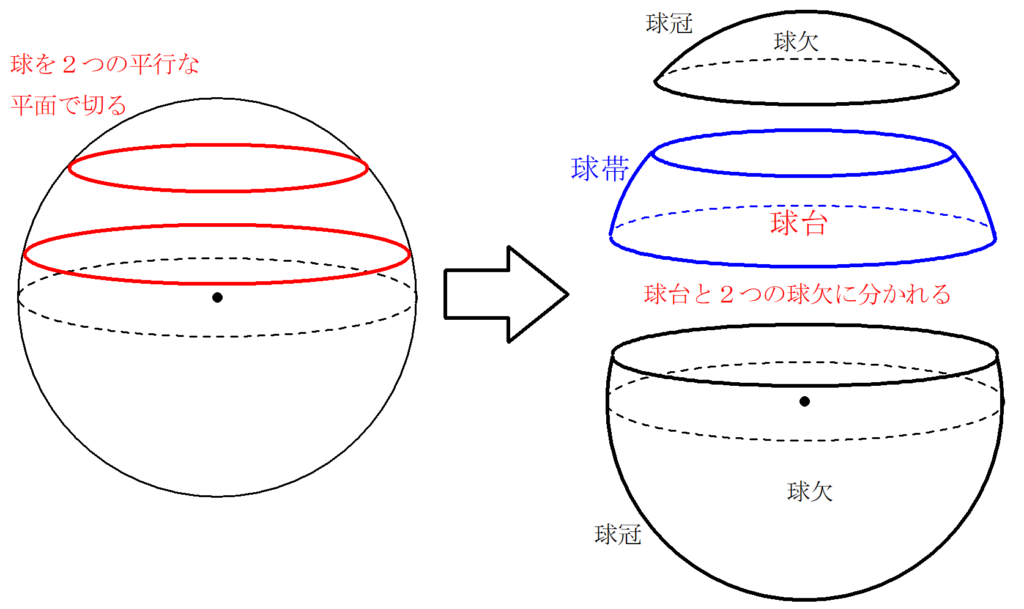
球台と球帯
球を2つの平面で切り取ってできた球台について考えます。 Ⅰ 球台と球帯とは? Ⅱ 球台の体積 Ⅲ 球帯の面積 【Ⅰ 球台と球帯とは?】 前記事の「球欠と球冠」同様... -

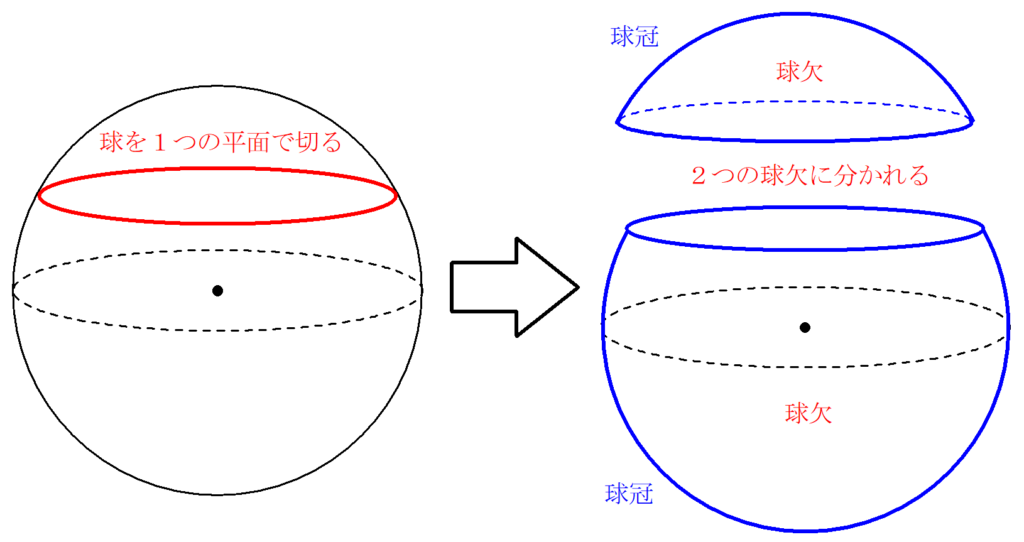
球欠と球冠
球を1つの平面で切り取ってできる球欠という立体について解説します。球欠の体積は、もとの球の半径に依存しない点が面白いです。 -

複素数の三角関数
$~\sin{x}~$が、$~\sin{z}~$だったら? 複素数の三角関数の定義や成り立つ公式、実数のときとの違いについて解説します。 -

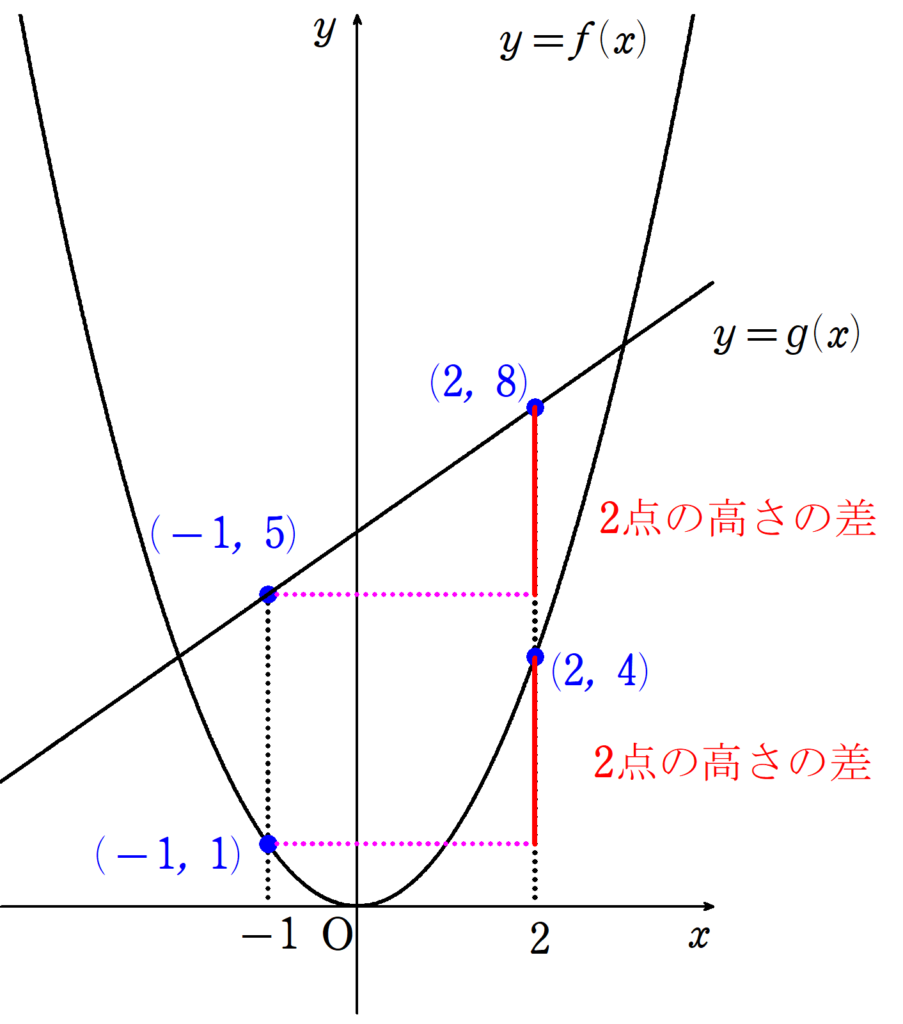
コーシーの平均値の定理
数学Ⅲで、「平均値の定理」を学びますが、本記事の「コーシーの平均値の定理」は、その一般化ともいえる定理となっています。それを例を交えて解説・証明していきます... -

無限多重根号②(計算結果編)
根号($ \sqrt{\quad}$)の中に根号($ \sqrt{\quad}$)、さらにその中にも根号($ \sqrt{\quad}$)・・・。 高校数学では二重根号まで習いますが、今回は無限に根... -

無限多重根号①(解法編)
根号($ \sqrt{\quad}$)の中に根号($ \sqrt{\quad}$)、さらにその中にも根号($ \sqrt{\quad}$)・・・。 高校数学では二重根号まで習いますが、今回は無限に根...