平面図形– tag –
-

ユークリッド幾何学の公理と公準を解説!理解しておきたい平行線公準とは?
ユークリッド幾何学の基本概念と5つの公準を解説。平行線の公準や三角形の合同条件など、幾何学の基礎を分かりやすく説明。数学の歴史や非ユークリッド幾何学についても触れ、幾何学の奥深さを探ります。 -

メナイクモスが円錐曲線を導入!立方体倍積問題の解法を解説!【数学史6-19】
この記事では、古代ギリシャの数学者メナイクモスが立方体倍積問題を解くために円錐曲線を初めて使用したことを解説しています。メナイクモスは平面を異なる角度で切断することで、放物線、楕円、双曲線などを生み出し、これらを用いて立方体の体積を倍にする問題に取り組みました。 -

ディノストラトスはプラトンの弟子の1人!彼が残した数学的功績を解説!【数学史6-18】
ディノストラトスはプラトンの弟子の一人であり、古代ギリシャの三大作図問題の1つである円積問題を研究した数学者です。彼の最も有名な業績はヒッピアスの円積線(クアドラトリクス)を円積問題に利用したこと。この記事では、その方法とディノストラトスの生涯について解説しています。 -

数学者のヒッピアスは円以外の曲線の発明者!円積線で三大作図問題が解ける!【数学史6-12】
三大作図問題の1つである「角の三等分問題」。この問題に初めて一定の成果を出したのは、古代ギリシャの数学者ヒッピアスでした。彼が発明した「円積線」を使うことで、角の三等分線は簡単に引くことができます。この記事では、ヒッピアスの人生について触れるとともに、円積線について細かく解説。円積線を式で表したり、なぜ円積線で角の三等分線が引けるのかを証明します。 -

数学者のヒポクラテスって何した人?ヒポクラテスの定理についても解説!【数学史6-10】
三日月図形の研究で有名な、古代ギリシャの数学者ヒポクラテス。円の面積と等しい正方形を作図する難問「円積問題」に取り組む中で、月形という曲線図形を直線図形に変形する術を思いつきました。この記事では、月形をはじめとするヒポクラテスの功績だけでなく、ヒポクラテスの不運なエピソードについてまで解説します。 -

「円周率の新しい求め方」ではない?話題の論文をざっくり解説!
2023年5月23日、高校生4人が円周率の新しい求め方を証明したという記事が、神戸新聞より掲載されました。しかし、その高校生たちが英語で書いた論文のタイトルは「円に内接する多角形の中で、面積が最大になるのは正多角形であることの初等的な証明」となっています。この記事では、その論文の内容をざっくりと解説!メディアの誇張に騙されないよう、論文の中身を大まかに理解しましょう。 -

三平方の定理の証明⑯~2023年最新!三角比を用いた証明をわかりやすく解説! 発見者は10代の少女?~
この記事では、数ある三平方の定理の証明の中でも、2023年最新の証明方法を紹介します。循環論法になりやすい三角比を使った珍しい証明方法です。話題になっている方法をどこよりもていねいに解説しています。 -

ヒポクラテスの三日月~定理の内容や証明をわかりやすく解説!応用例も紹介!~
中学受験で登場する「ヒポクラテスの定理」。この定理は今から約2500年前に生まれ、曲線図形の面積が直線図形の面積と等しくなるという観点から、当時のギリシャに大きな衝撃を与えました。この記事では、その歴史について触れながらも定理の内容やその証明、応用例について解説します。 -

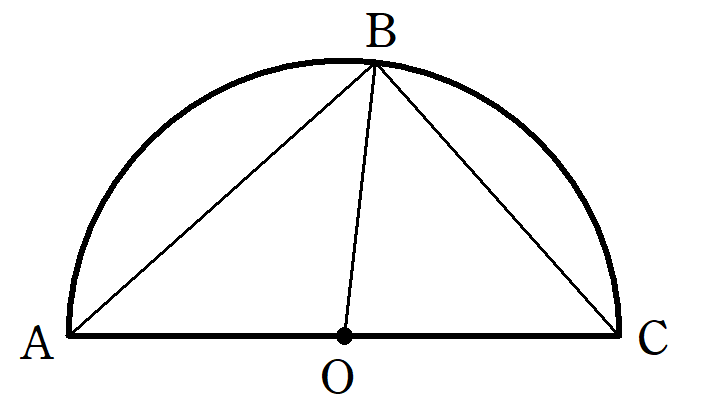
タレスの定理~中学3年生で習う円の定理を解説!証明は超簡単!~
世界で最初に証明された定理は「タレスの定理」であり、「半円に内接する三角形は直角三角形である」という内容です。実は、タレスの定理と呼ばれる定理は他にもあり、すべて現在の中学レベルの内容でした。それらの紹介と共に、タレスの定理が後世の数学にどのような影響を与えたのかを解説します。 -

三平方の定理の証明を16種類紹介! 由来や歴史、対象学年まで掲載
100種類以上あると言われる三平方の定理の証明の中から有名なものを抜粋。さらに、必要な予備知識の対象学年で、証明を分類。証明の複雑さや美しさも、主観で5段階評価しました。この記事を読むことで、自分に合った三平方の定理の証明方法が見つけられます。