15°の三角比は近似値を使わずに、値を表すことができます。
その値とは、以下の通り。
\begin{align*}
\sin{15^{\circ}}&=\frac{\sqrt{6}-\sqrt{2}}{4} \\
\\
\cos{15^{\circ}}&=\frac{\sqrt{6}+\sqrt{2}}{4} \\
\\
\tan{15^{\circ}}&=2-\sqrt{3} \\
\end{align*}この記事では、これらの値がどのように求まるのかを、現役数学教員が解説。
15°の三角比は、三角関数の加法定理や半角の公式のみならず、直角三角形から図形的に求めることもできます。
- 15°の三角比の値とその近似値
- 三角関数の加法定理を利用した求め方
- 半角の公式を利用した求め方
- 直角三角形を利用した求め方
マイナーな三角比の値を含めた、三角比の値一覧表はこちらから↓↓
15°の三角比の値とその近似値
15°の三角比の値
$~15^{\circ}=\displaystyle \frac{\pi}{12}~$の三角比の値は以下のように表されます。
\begin{align*}
\sin{15^{\circ}}&=\displaystyle \frac{\sqrt{6}-\sqrt{2}}{4} \\
\\
\cos{15^{\circ}}&=\frac{\sqrt{6}+\sqrt{2}}{4} \\
\\
\tan{15^{\circ}}&=2-\sqrt{3}
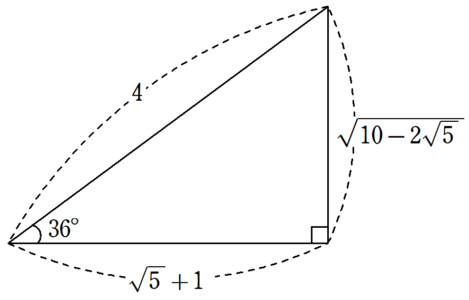
\end{align*}二重根号が出てこないため、15° , 75°の直角三角形の辺の比で考えれば、図1のようになります。
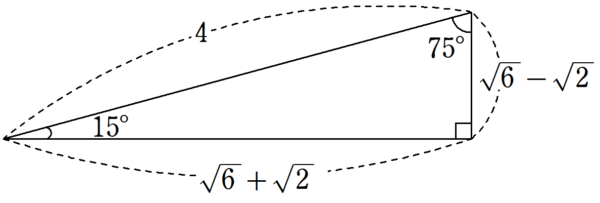

高校受験では、この比を知っていると解きやすい問題が、難関私立を中心によく出てくるよ!
15°の三角比の近似値
15°の三角比の値 の近似値ををExcelで出してみると、図2のようになります。
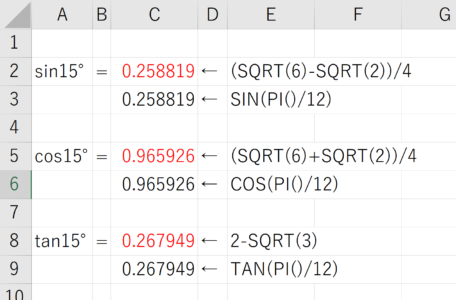

小数第5位を四捨五入すると、教科書に載っている三角比の値と同じ数値が出てきます。
エクセルの関数で求めたものとも見事に一致しています。



当然っちゃ、当然。
15°の三角比の求め方
三角関数の加法定理と半角の公式は数学Ⅱで学習しますが、直角三角形を利用する方法であれば数学Ⅰの知識で理解することができます。
三角関数の加法定理による求め方
$~15^{\circ}=45^{\circ}-30^{\circ}~$であることを利用し、三角関数の加法定理を使うだけの方法です。
- $~\sin{15^{\circ}}~$の値
三角関数の加法定理$~\sin{(\alpha-\beta)}=\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}~$で、$~\alpha=45^{\circ}~,~\beta=30^{\circ}~$とすると、
\begin{align*}
\sin{15^{\circ}}&=\displaystyle \sin{(45^{\circ}-30^{\circ})} \\
\\
&=\sin{45^{\circ}}\cos{30^{\circ}}-\cos{45^{\circ}}\sin{30^{\circ}} \\
\\
&=\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}\cdot \frac{1}{2} \\
\\
&=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4} \\
\\
&=\frac{\sqrt{6}-\sqrt{2}}{4}
\end{align*}が求まる。
- $~\cos{15^{\circ}}~$の値
三角関数の加法定理$~\cos{(\alpha-\beta)}=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}~$で、$~\alpha=45^{\circ}~,~\beta=30^{\circ}~$とすると、
\begin{align*}
\cos{15^{\circ}}&=\displaystyle \cos{(45^{\circ}-30^{\circ})} \\
\\
&=\cos{45^{\circ}}\cos{30^{\circ}}+\sin{45^{\circ}}\sin{30^{\circ}} \\
\\
&=\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot \frac{1}{2} \\
\\
&=\frac{\sqrt{6}}{4}+\frac{\sqrt{2}}{4} \\
\\
&=\frac{\sqrt{6}+\sqrt{2}}{4}
\end{align*}が求まる。
- $~\tan{15^{\circ}}~$の値
三角関数の加法定理$~\tan{(\alpha-\beta)}=\displaystyle \frac{\tan{\alpha}-\tan{\beta}}{1+\tan{\alpha}\tan{\beta}} ~$で、$~\alpha=45^{\circ}~,~\beta=30^{\circ}~$とすると、
\begin{align*}
\tan{15^{\circ}}&=\displaystyle \tan{(45^{\circ}-30^{\circ})} \\
\\
&=\frac{\tan{45^{\circ}}-\tan{30^{\circ}}}{1+\tan{45^{\circ}}\tan{30^{\circ}}} \\
\\
&=\frac{1-\frac{1}{\sqrt{3}}}{1+1\cdot \frac{1}{\sqrt{3}}} \\
\\
&=\frac{\sqrt{3}-1}{\sqrt{3}+1} \\
\\
&=\frac{(\sqrt{3}-1)(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)} \\
\\
&=\frac{4-2\sqrt{3}}{2} \\
\\
&=2-\sqrt{3}
\end{align*}が求まる。
そこまで複雑な計算をすることなく求めることができる方法でした。
半角の公式による求め方
15°は30°の半分であるため、半角の公式を使うだけでもOKです。
- $~\sin{15^{\circ}}~$の値
半角の公式$~\displaystyle \sin^2{\frac{\theta}{2}}=\frac{1-\cos{\theta}}{2}~$で、$~\theta=30^{\circ}~$とすると、
\begin{align*}
\sin^2{15^{\circ}}&=\frac{1-\cos{30^{\circ}}}{2} \\
\\
&=\frac{1-\frac{\sqrt{3}}{2}}{2} \\
\\
&=\frac{2-\sqrt{3}}{4} \\
\end{align*}となるため、 $~\sin{15^{\circ}} > 0~$より、
\begin{align*}
\sin{15^{\circ}}&=\frac{\sqrt{2-\sqrt{3}}}{2} \\
\\
&=\frac{\sqrt{2-\sqrt{3}}\cdot \sqrt{2}}{2\sqrt{2}} \\
\\
&=\frac{\sqrt{4-2\sqrt{3}}}{2\sqrt{2}} \\
\\
&=\frac{\sqrt{(\sqrt{3}-1)^2}}{2\sqrt{2}} \\
\\
&=\frac{|\sqrt{3}-1|}{2\sqrt{2}} \\
\\
&=\frac{(\sqrt{3}-1)\cdot \sqrt{2}}{2\sqrt{2}\cdot \sqrt{2}} \\
\\
&=\frac{\sqrt{6}-\sqrt{2}}{4}
\end{align*}が求まる。
- $~\cos{15^{\circ}}~$の値
半角の公式$~\displaystyle \cos^2{\frac{\theta}{2}}=\frac{1+\cos{\theta}}{2}~$で、$~\theta=30^{\circ}~$とすると、
\begin{align*}
\cos^2{15^{\circ}}&=\frac{1+\cos{30^{\circ}}}{2} \\
\\
&=\frac{1+\frac{\sqrt{3}}{2}}{2} \\
\\
&=\frac{2+\sqrt{3}}{4} \\
\end{align*}となるため、 $~\cos{15^{\circ}} > 0~$ より、
\begin{align*}
\cos{15^{\circ}}&=\frac{\sqrt{2+\sqrt{3}}}{2} \\
\\
&=\frac{\sqrt{2+\sqrt{3}}\cdot \sqrt{2}}{2\sqrt{2}} \\
\\
&=\frac{\sqrt{4+2\sqrt{3}}}{2\sqrt{2}} \\
\\
&=\frac{\sqrt{(\sqrt{3}+1)^2}}{2\sqrt{2}} \\
\\
&=\frac{|\sqrt{3}+1|}{2\sqrt{2}} \\
\\
&=\frac{(\sqrt{3}+1)\cdot \sqrt{2}}{2\sqrt{2}\cdot \sqrt{2}} \\
\\
&=\frac{\sqrt{6}+\sqrt{2}}{4}
\end{align*}が求まる。
- $~\tan{15^{\circ}}~$の値
半角の公式$~\displaystyle \tan^2{\frac{\theta}{2}}=\frac{ 1-\cos{\theta} }{1+\cos{\theta}}~$で、$~\theta=30^{\circ}~$とすると、
\begin{align*}
\tan^2{15^{\circ}}&=\frac{1-\cos{30^{\circ}}}{1+\cos{30^{\circ}}} \\
\\
&=\frac{1-\frac{\sqrt{3}}{2}}{1+\frac{\sqrt{3}}{2}} \\
\\
&=\frac{2-\sqrt{3}}{2+\sqrt{3}} \\
\\
&=\frac{(2-\sqrt{3})(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})} \\
\\
&=\frac{(2-\sqrt{3})^2}{4-3} \\
\\
&=(2-\sqrt{3})^2
\end{align*}となるため、 $~\tan{15^{\circ}} > 0~$ より、
\begin{align*}
\tan{15^{\circ}}&=|2-\sqrt{3}|
\\
&=2-\sqrt{3}
\end{align*}が求まる。
$~\sin{15^{\circ}}~$と$~\cos{15^{\circ}}~$は二重根号が出てくるという点で、計算力がないと難しいです。



まさかの$~\tan{15^{\circ}}~$の計算が一番あっさり!
直角三角形による求め方
最後の方法は、二重根号の処理や分母の有理化さえできれば中3でも理解できるレベルの求め方。
15°,75°の直角三角形をうまく使います。
図3の直角三角形で考える。
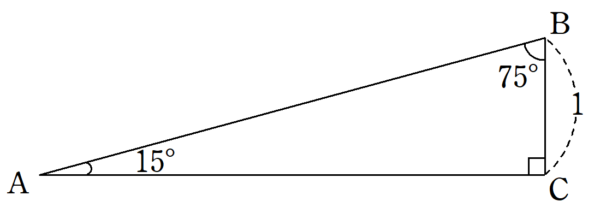

$~\angle DBC=60^{\circ}~$となるように、$~AC~$上に$~D~$をとると、$~\triangle DBC~$は 30°、60°、90° の直角三角形となり、また$~\triangle DAB~$は 15°、15°、150° の二等辺三角形となる。
このとき、図4のように長さがわかる。
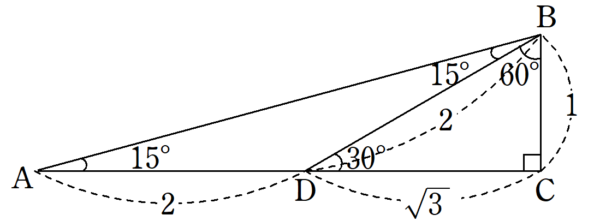

ここで、三平方の定理より、
\begin{align*}
AB^2&=1^2+(2+\sqrt{3})^2 \\
&=1+4+4\sqrt{3}+3 \\
&=8+4\sqrt{3}
\end{align*}であり、両辺正の平方根をとると、
\begin{align*}
AB&=\sqrt{8+4\sqrt{3}} \\
&=\sqrt{8+2\sqrt{12}} \\
&=\sqrt{(\sqrt{6}+\sqrt{2})^2} \\
&=\sqrt{6}+\sqrt{2}
\end{align*}と求まる。
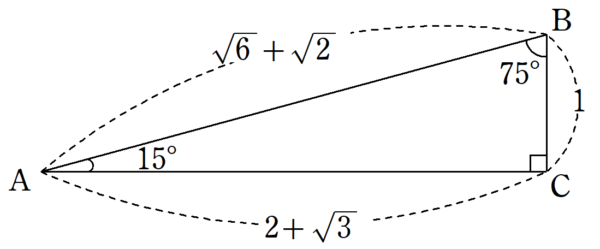

図5から、三角比の値は、
\begin{align*}
\sin{15^{\circ}}&=\displaystyle \frac{1}{\sqrt{6}+\sqrt{2}} \\
\\
&=\frac{1\cdot (\sqrt{6}-\sqrt{2})}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})} \\
\\
&=\frac{\sqrt{6}-\sqrt{2}}{4} \\
\end{align*}\begin{align*}
\cos{15^{\circ}}&=\displaystyle \frac{2+\sqrt{3}}{\sqrt{6}+\sqrt{2}} \\
\\
&=\frac{(2+\sqrt{3})(\sqrt{6}-\sqrt{2})}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})} \\
\\
&=\frac{2\sqrt{6}-2\sqrt{2}+3\sqrt{2}-\sqrt{6}}{4} \\
\\
&=\frac{\sqrt{6}+\sqrt{2}}{4} \\
\end{align*}\begin{align*}
\tan{15^{\circ}}&=\displaystyle \frac{1}{2+\sqrt{3}} \\
\\
&=\frac{1\cdot (2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})} \\
\\
&=\frac{2-\sqrt{3}}{1} \\
\\
&=2-\sqrt{3}
\end{align*}と求まる。
二重根号や分母の有理化が面倒ではあるものの、図形的な性質をうまく使って求めることができる方法でした。
ちなみに、次のような図を使っても求めることができます。
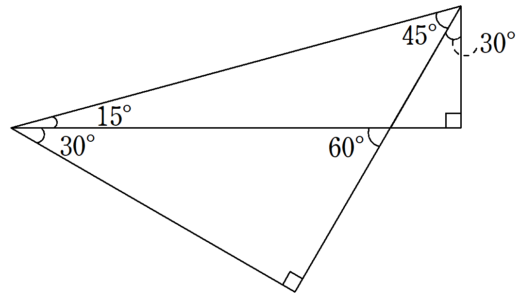




公式の中に、二重根号が無いってステキ!



教科書で覚える三角比の値以外では、一番キレイで実用的。
15° , 75° の直角三角形の辺の比を覚えてしまおう!
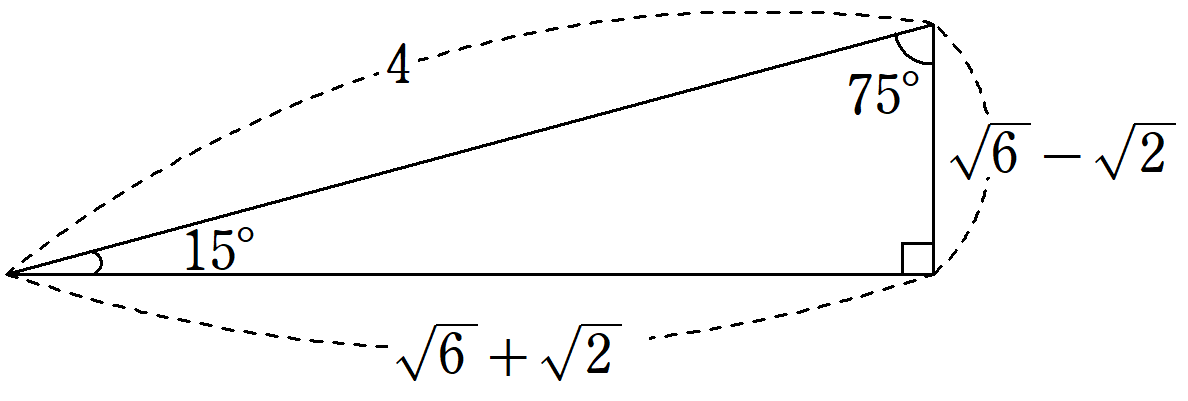
コメント
コメント一覧 (4件)
半角の公式でtan15°を求めるところの文頭が、tan18°となっています。
いたすと3様
ご指摘いただきありがとうございます。
大事な部分での誤字に気付いておらず、大変助かりました。
今後ともどうぞよろしくお願いします。
Fukusuke
15°の三角比
最初の枠内で、
cos15°、tan15°
とすべきところが
cos36°、tan36°
になってます。
コメントありがとうございます。
修正したしました!!
大事なまとめの部分でお恥ずかしい・・・。