22.5°の三角比は近似値を使わずに、値を表すことができます。
その値とは、以下の通り。
\begin{align*}
\sin{22.5^{\circ}}&=\frac{\sqrt{2-\sqrt{2}}}{2} \\
\\
\cos{22.5^{\circ}}&=\frac{\sqrt{2+\sqrt{2}}}{2} \\
\\
\tan{22.5^{\circ}}&=\sqrt{2}-1
\end{align*}この記事では、これらの値がどのように求まるのかを、現役数学教員が2通りの方法で解説。
数学Ⅱで学ぶ「半角の公式」を使わずに、図形から値を求めることができるんです!!
- 22.5°の三角比の値とその近似値
- 半角の公式を使った求め方
- 図形を使った求め方
マイナーな三角比の値を含めた、三角比の値一覧表はこちらから↓↓
22.5°の三角比の値とその近似値
22.5°の三角比の値
$~22.5^{\circ}=\displaystyle \frac{\pi}{8}~$の三角比の値は、二重根号を用いて以下のように表されます。
\begin{align*}
\sin{22.5^{\circ}}&=\sin{\frac{\pi}{8}}=\frac{\sqrt{2-\sqrt{2}}}{2} \\
\\
\cos{22.5^{\circ}}&=\cos{\frac{\pi}{8}}=\frac{\sqrt{2+\sqrt{2}}}{2} \\
\\
\tan{22.5^{\circ}}&=\tan{\frac{\pi}{8}}=\sqrt{2}-1
\end{align*}複雑な式というわけではないため、覚えようと思えば暗記することもできそうです。

$~\sin{}~$と $~\cos{}~$は形が似ているし、$~2~$しか出てこない!
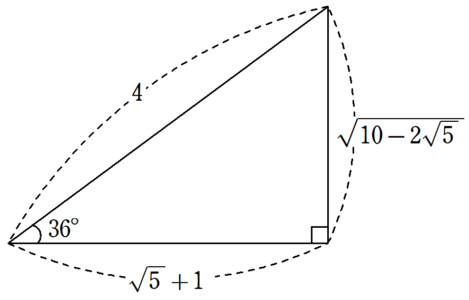
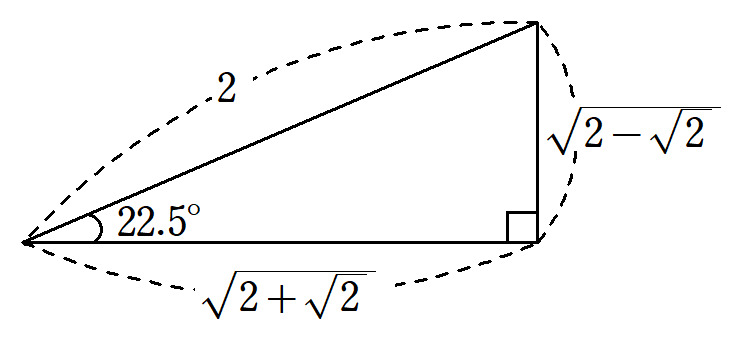
これらの値を基に、斜辺が$~2~$の直角三角形で作ると、図1のようになります。
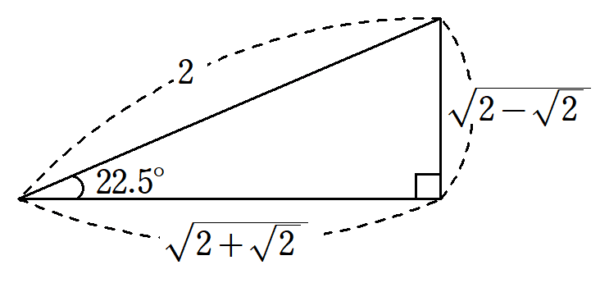

22.5°の三角比の近似値
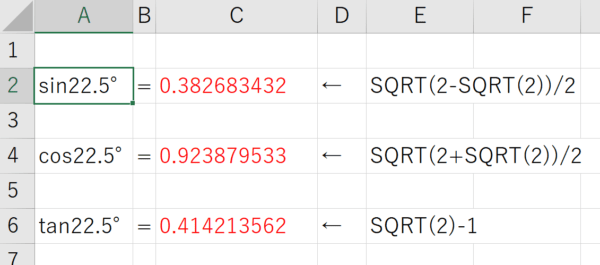
22.5°の三角比の値 の近似値ををExcelで出してみると、図2のようになります。

三角比の表に載っている22°と23°の三角比の値(表3)から、22.5°の三角比の近似値の妥当性がわかります。
| 三角比 | 22° | 23° |
| 正弦($\sin{}$) | 0.3746 | 0.3907 |
| 余弦($\sin{}$) | 0.9272 | 0.9205 |
| 正接($\sin{}$) | 0.4040 | 0.4245 |
22.5°の三角比の求め方
半角の公式による求め方
数学Ⅱで学ぶ半角の公式を使うことで、簡単に証明できます。



22.5°は45°の半分!
- $~\sin{22.5^{\circ}}~$の値
半角の公式$~\displaystyle \sin^2{\frac{\theta}{2}}=\frac{1-\cos{\theta}}{2}~$で、$~\theta=45^{\circ}~$とすると、
\begin{align*}
\sin^2{22.5^{\circ}}&=\frac{1-\cos{45^{\circ}}}{2} \\
\\
&=\frac{1-\frac{1}{\sqrt{2}}}{2} \\
\\
&=\frac{\sqrt{2}-1}{2\sqrt{2}} \\
\\
&=\frac{(\sqrt{2}-1)\cdot \sqrt{2}}{2\sqrt{2}\cdot \sqrt{2}} \\
\\
&=\frac{2-\sqrt{2}}{4} \\
\end{align*}となるため、 $~\sin{22.5^{\circ}} > 0~$より、
\sin{22.5^{\circ}}=\frac{\sqrt{2-\sqrt{2}}}{2} が求まる。
- $~\cos{22.5^{\circ}}~$の値
半角の公式$~\displaystyle \cos^2{\frac{\theta}{2}}=\frac{1+\cos{\theta}}{2}~$で、$~\theta=45^{\circ}~$とすると、
\begin{align*}
\cos^2{22.5^{\circ}}&=\frac{1+\cos{45^{\circ}}}{2} \\
\\
&=\frac{1+\frac{1}{\sqrt{2}}}{2} \\
\\
&=\frac{\sqrt{2}+1}{2\sqrt{2}} \\
\\
&=\frac{(\sqrt{2}+1)\cdot \sqrt{2}}{2\sqrt{2}\cdot \sqrt{2}} \\
\\
&=\frac{2+\sqrt{2}}{4} \\
\end{align*}となるため、 $~\cos{22.5^{\circ}} > 0~$ より、
\cos{22.5^{\circ}}=\frac{\sqrt{2+\sqrt{2}}}{2} が求まる。
- $~\tan{22.5^{\circ}}~$の値
半角の公式$~\displaystyle \tan^2{\frac{\theta}{2}}=\frac{ 1-\cos{\theta} }{1+\cos{\theta}}~$で、$~\theta=45^{\circ}~$とすると、
\begin{align*}
\tan^2{22.5^{\circ}}&=\frac{1-\cos{45^{\circ}}}{1+\cos{45^{\circ}}} \\
\\
&=\frac{1-\frac{1}{\sqrt{2}}}{1+\frac{1}{\sqrt{2}}} \\
\\
&=\frac{\sqrt{2}-1}{\sqrt{2}+1} \\
\\
&=\frac{(\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)} \\
\\
&=\frac{(\sqrt{2}-1)^2}{2-1} \\
\\
&=(\sqrt{2}-1)^2
\end{align*}となるため、 $~\tan{22.5^{\circ}} > 0~$ より、
\tan{22.5^{\circ}}=|\sqrt{2}-1|=\sqrt{2}-1が求まる。
機械的ではありますが、$~\cos{45^{\circ}}~$を代入するだけで求めることができました。
図形による求め方
こちらは、$~22.5^{\circ}~,~67.5^{\circ}~,~90^{\circ}~$の直角三角形の中に、直角二等辺三角形を作ることで、幾何的に求めることができます。
$~22.5^{\circ}~,~67.5^{\circ}~,~90^{\circ}~$からなる直角三角形$~ABC~$を考える。
$~BC~$上に$~\angle DAC=45^{\circ}~$となるように点$~D~$をとる。
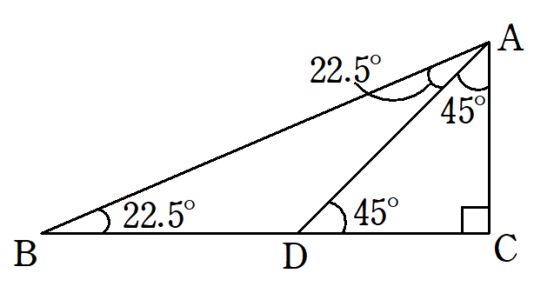

$~AC=1~$とするとき、直角二等辺三角形$~ADC~$と二等辺三角形$~DBA~$により、図5のように長さがわかる。
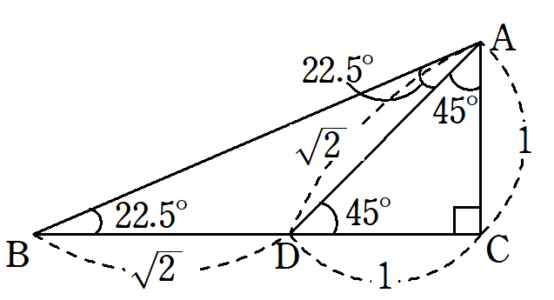

ここで、$~\triangle ABC~$で三平方の定理を使うと、
\begin{align*}
AB^2&=1^2+(\sqrt{2}+1)^2 \\
&=1+2\sqrt{2}+1 \\
&=4+\sqrt{2}
\end{align*}であり、$~AB > 0~$なので、
AB=\sqrt{4+2\sqrt{2}}と求まる。
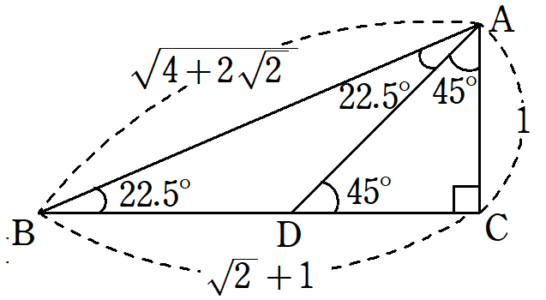

よって、図6からそれぞれの三角比を求めると、
\begin{align*}
\sin{22.5^{\circ}}&=\frac{1}{\sqrt{4+2\sqrt{2}}} \\
\\
&=\frac{1}{\sqrt{2}\sqrt{2+\sqrt{2}}} \\
\\
&=\frac{1 \cdot \sqrt{2-\sqrt{2}}}{\sqrt{2}\sqrt{2+\sqrt{2}} \cdot \sqrt{2-\sqrt{2}}} \\
\\
&=\frac{\sqrt{2-\sqrt{2}}}{\sqrt{2}\sqrt{(2+\sqrt{2})(2-\sqrt{2})}} \\
\\
&=\frac{\sqrt{2-\sqrt{2}}}{\sqrt{2}\sqrt{4-2}} \\
\\
&=\frac{\sqrt{2-\sqrt{2}}}{\sqrt{2}\sqrt{2}} \\
\\
&=\frac{\sqrt{2-\sqrt{2}}}{2} \\
\end{align*}\begin{align*}
\cos{22.5^{\circ}}&=\frac{\sqrt{2}+1}{\sqrt{4+2\sqrt{2}}} \\
\\
&=\frac{\sqrt{2}+1}{\sqrt{2}\sqrt{2+\sqrt{2}}} \\
\\
&=\frac{(\sqrt{2}+1)\sqrt{2-\sqrt{2}}}{\sqrt{2}\sqrt{2+\sqrt{2}} \cdot \sqrt{2-\sqrt{2}}} \\
\\
&=\frac{\sqrt{(\sqrt{2}+1)^2(2-\sqrt{2})}}{\sqrt{2}\sqrt{(2+\sqrt{2})(2-\sqrt{2})}} \\
\\
&=\frac{\sqrt{(3+2\sqrt{2})(2-\sqrt{2})}}{\sqrt{2}\sqrt{4-2}} \\
\\
&=\frac{\sqrt{6-3\sqrt{2}+4\sqrt{2}-4}}{\sqrt{2}\sqrt{2}} \\
\\
&=\frac{\sqrt{2+\sqrt{2}}}{2} \\
\end{align*}\begin{align*}
\tan{22.5^{\circ}}&=\frac{1}{\sqrt{2}+1} \\
\\
&=\frac{1\cdot (\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)} \\
\\
&=\frac{\sqrt{2}-1}{2-1} \\
\\
&=\sqrt{2}-1
\end{align*}と計算できた。■
直角三角形の各辺の長さを求めること自体は簡単ですが、二重根号を分母に持つ分数の式変形が大変でした。



図形による解き方は、数学Ⅰのレベルでも解けるけど、多項式の有理化や二重根号といった難度の高い計算が目白押しだね。



半角の公式って、地味に便利だよね。
コメント
コメント一覧 (1件)
ありがとうございます