36°の三角比は近似値を使わずに、値を表すことができます。
その値とは、以下の通り。
\begin{align*}
\sin{36^{\circ}}&=\frac{\sqrt{10-2\sqrt{5}}}{4} \\
\\
\cos{36^{\circ}}&=\frac{\sqrt{5}+1}{4} \\
\\
\tan{36^{\circ}}&=\sqrt{5-2\sqrt{5}}
\end{align*}この記事では、これらの値がどのように求まるのかを、現役数学教員が解説。
黄金比を計算することで、36°の三角比の値がわかるんです!
- 36°の三角比の値とその近似値
- 黄金三角形を利用した求め方
マイナーな三角比の値を含めた、三角比の値一覧表はこちらから↓↓
36°の三角比の値とその近似値
36°の三角比の値
$~36^{\circ}=\displaystyle \frac{\pi}{5}~$の三角比の値は、二重根号を用いて以下のように表されます。
\begin{align*}
\sin{36^{\circ}}&= \frac{\sqrt{10-2\sqrt{5}}}{4} \\
\\
\cos{36^{\circ}}&= \frac{\sqrt{5}+1}{4} \\
\\
\tan{36^{\circ}}&=\sqrt{5-2\sqrt{5}} \\
\end{align*}$~\cos{36^{\circ}}~$だけは、二重根号がなくスッキリとした式になっています。

$~\sin{}~$と$~\tan{}~$は複雑‥‥。
二重根号だから、近似値の見当もつかない。
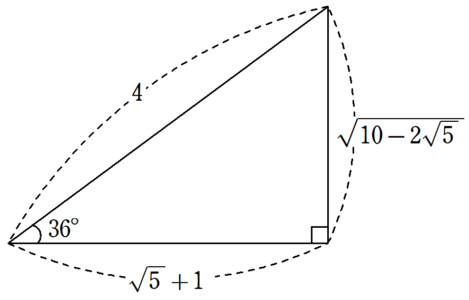
これらの値を基に、斜辺が$~4~$の直角三角形で作ると、図1のようになります。


36°の三角比の近似値
36°の三角比の値 の近似値ををExcelで出してみると、図2のようになります。
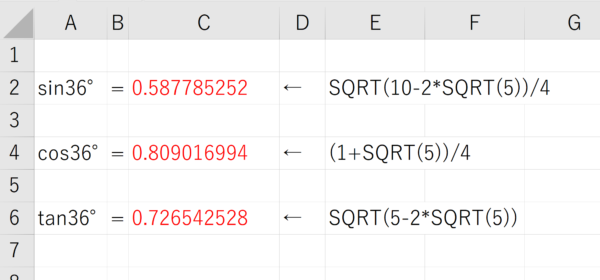

小数第5位を四捨五入すると、教科書に載っている三角比の値と同じ数値が出てきます。
黄金比による求め方
36°の三角比を求める際に使う図は、36°、72°、72°の二等辺三角形です。
この二等辺三角形は黄金三角形と呼ばれ、正五角形や黄金比に大きく関わる三角形になります。


cos36°を求める
まずは、$~\cos{36^{\circ}}~$の値から求めます。
図3のような$~AB=AC=1~,~\angle{A}=36°~$の$~\triangle ABC~$を考える。
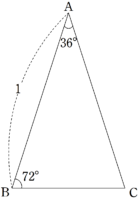

$~\angle{B}~$の二等分線と$~AC~$の交点を$~D~$とする。
このとき、$~\triangle DAB~$や$~\triangle BCD~$も二等辺三角形となるので、$~BC=x~$とすると、$~BD~$や$~AD~$も$~x~$となる。
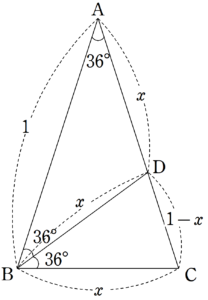

$~\triangle ABC~$∽$~ \triangle BCD~$より、
\begin{align*}
1:x&=x:(1-x) \\
x^2&=1-x \\
x^2+x-1&=0 \\
x&=\frac{-1 \pm \sqrt{5}}{2}
\end{align*}$~x > 0~$より、$~x=\displaystyle \frac{-1 + \sqrt{5}}{2}~$。
次に、$~B~$から$~AC~$におろした垂線の足を$~E~$とすると、$~E~$は$~DC~$の中点となるので、$~\displaystyle DE=\frac{1-x}{2}~$となる。
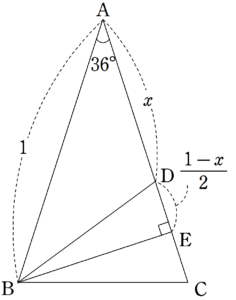

直角三角形 $~BEA~$ に注目すれば、
\begin{align*}
\cos{36^{\circ}}&=\frac{AE}{1} \\
\\
&=AE \\
\\
&=\displaystyle x+\frac{1-x}{2} \\
\\
&=\frac{x}{2}+\frac{1}{2} \\
\\
&=\frac{-1 \pm \sqrt{5}}{4}+\frac{1}{2} \\
\\
&=\frac{1 \pm \sqrt{5}}{4}
\end{align*}であり、$~\cos{36^{\circ}} > 0~$より、
\cos{36^{\circ}}=\displaystyle \frac{\sqrt{5}+1}{4}と求まった。■
ちなみに、 1辺$~1~$の正五角形の対角線$~x=\displaystyle \frac{-1 + \sqrt{5}}{2}~$こそが黄金数であり、$~1~:~x~$のことを黄金比と言います。
sin36°とtan36°を求める
$~\sin^2{36^{\circ}}+\cos^2{36^{\circ}}=1~$より、
\begin{align*}
\sin^2{36^{\circ}}&=1-\displaystyle \left( \frac{1+\sqrt{5}}{4} \right)^2 \\
\\
&=1-\frac{1+2\sqrt{5}+5}{16} \\
\\
&=\frac{10-2\sqrt{5}}{16}
\end{align*}であり、$~\sin{36^{\circ}} > 0~$より、
\sin{36^{\circ}}=\frac{\sqrt{10-2\sqrt{5}}}{4}と求まった。■



もちろん、図5の$~\triangle ABE~$で三平方の定理を使って、$~BE=\sin{36^{\circ}}~$を求めることもできます。
$~1+\tan^2{36^{\circ}}=\displaystyle \frac{1}{\cos^2{36^{\circ}}}~$より、
\begin{align*}
\tan^2{36^{\circ}}&=\displaystyle \left( \frac{4}{1+\sqrt{5}} \right)^2-1 \\
\\
&=\frac{16}{6+2\sqrt{5}}-1 \\
\\
&=\frac{16(6-2\sqrt{5})}{(6+2\sqrt{5})(6-2\sqrt{5})}-1 \\
\\
&=\frac{16(6-2\sqrt{5})}{16}-1 \\
\\
&=6-2\sqrt{5}-1 \\
\\
&=5-2\sqrt{5}
\end{align*}であり、$~\tan{36^{\circ}} > 0~$ より、
\tan{36^{\circ}}=\displaystyle \sqrt{5-2\sqrt{5}}と求まった。■



こちらについても、$~\tan{36^{\circ}}=\displaystyle \frac{ \sin{36^{\circ}} }{ \cos{36^{\circ}} }~$を利用して求めてもOKです。



こうしてみると、黄金比って美しくないね。



あくまで黄金比に基づいた形が、人間にとって美しく見えるだけだからね。数値自体は、無理数ゆえに複雑なんだ。
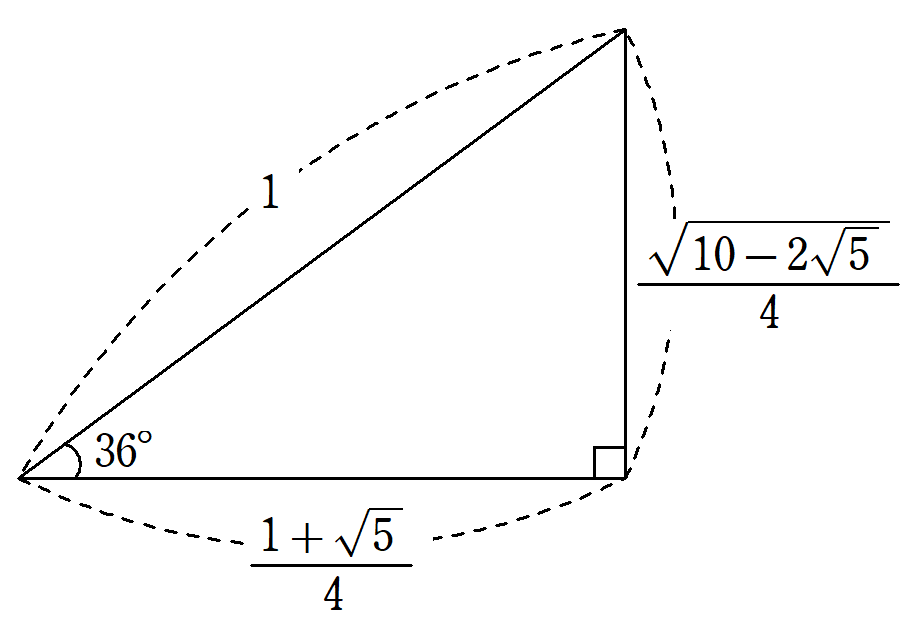
コメント