基礎例題と問題解説で数学Ⅰを教科書の流れで理解する「れいもん」。
今回は多項式の加法、減法、乗法についての用語や計算方法を理解しましょう。
- 多項式の加法と減法について
- 多項式の乗法、指数法則について
- 展開の公式について
- 式の計算の工夫について
「れいもん」では、数研出版の検定済教科書『数学Ⅰ』の流れに沿って、例題と問題を解説しています。
手書きの解説は、タップすることで拡大することができます。
多項式の計算法則
交換法則 $~A+B=B+A,AB=BA~$
結合法則 $~(A+B)+C=A+(B+C),(AB)C=A(BC)~$
分配法則 $~A(B+C)=AB+BC,(A+B)C=AC+BC~$
多項式の加法、減法、乗法は、数の場合と同様に、上記の計算法則を基礎として行われます。
さらに、式の計算の工夫を加えることで、複雑な式の計算も分かりやすく計算できるのです。

本当かなぁ……?
この計算法則を覚えるだけでも大変だよ……。
1-2-A 多項式の加法・減法
多項式の和と差は、同類項をまとめることによって計算できます。
差を求める減法では、マイナスによって、後ろの多項式の符号が変わりますので、計算ミスに注意して求めましょう。



ただでさえ複雑な多項式同士を計算するのかぁ……。
多項式の和と差を求める計算
では、実際に例題を見ながら、多項式の和と差を求めてみましょう。
(1) 和を求める問題
\begin{align*}
(4x^3-2x^2+5x-7)+(3x^3-6x-8)&=4x^3-2x^2+5x-7+3x^3-6x-8\\
&=(4+3)x^3-2x^2+(5-6)x+(-7-8)\\
&=7x^3-2x^2-x-15
\end{align*}(2) 差を求める問題
\begin{align*}
(4x^3-2x^2+5x-7)-(3x^3-6x-8)&=4x^3-2x^2+5x-7-3x^3+6x+8\\
&=(4-3)x^3-2x^2+(5+6)x+(-7+8)\\
&=x^3-2x^2-11x+1
\end{align*}


ふう……。
和と差を求めるだけでも項が多いから一苦労だね。



差を求める時に、符号の変化に注意して解けたね。
計算の最後は、降べきの順に項を並べるのが一般的だよ。
文字による置き換え
多項式を計算する時には、多項式を1つずつ別の文字に置き換えることで、計算式がシンプルに。
計算式がシンプルになることで、計算も楽になり、ミスも少なくすることができます。
手順としては、まず置き換えた文字同士で式の計算をし、そのあとに多項式を代入します。
では早速、例題で確認してみましょう。
$~A=2x^3-4xy^2-y^3,B=-x^2y+5xy^2+2y^3,C=x^3+x^2y~$であるとき、$~A-3(B-C)+4C~$を計算せよ。
\begin{align*}
A-3(B-C)+4C&=A-3B+3C+4C\\
&=A-3B+7C\\
&=(2x^3-4xy^2-y^3)-3(-x^2y+5xy^2+2y^3)+7(x^3+x^2y)\\
&=2x^3-4xy^2-y^3+3x^2y-15xy^2-6y^3+7x^3+7x^2y\\
&=(2+7)x^3+(3+7)x^2y+(-4-15)xy^2+(-1-6)y^3\\
&=9x^3+10x^2y-19xy^2-7y^3
\end{align*}


まずは大文字に置き換えられた式を整理して、多項式を代入すればいいんだね!



慌てずに落ち着いて、大文字の式を整理して簡単にしていこう。
1-2-B 多項式の乗法
今回も覚えるべき用語や公式がいくつかあります。
この先の数学でも当たり前のように出てくる用語や公式なので、しっかり覚えましょう。
- 累乗‥‥同じ文字をいくつか掛けたもの。$~a~$を$~n~$個掛けた累乗を$~a~$の$~n~$乗といい$~a^n~$と書く。
- 指数‥‥$~a^n~$における$~n~$のこと。
一般に、次の指数法則が成り立ちます。
$~m,n~$は正の整数とする。
(1) $~a^ma^n=a^{m+n}~$
(2) $~(a^m)^n=a^{mn}~$
(3) $~(ab)^n=a^nb^n~$



ただの乗法なのか、累乗なのか、よく注意しよう!
指数法則を用いた単項式の積
単項式の積は、指数法則を使って、次のように計算します。
次の計算をせよ。
$~(1) 3a^2\times 7a^3~$
$~(2) 4x^3yz^2\times2xy^4z^3~$
$~(3) (2x^2y^3)^2\times(-3x^3y^2)~$
(1)
\begin{align*}
3a^2\times7a^3&=(3\times7)a^{2+3}\\
&=21a^5\\
\end{align*}(2)
\begin{align*}
4x^3yz^2\times2xy^4z^3&=(4\times2)x^{3+1}y^{1+4}z^{2+3}\\
&=8x^4y^5z^5\\
\end{align*}(3)
\begin{align*}
(2x^2y^3)^2\times(-3x^3y^2)&=2^2(x^2)^2(y^3)^2\times(-3)x^3y^2\\
&=4x^4y^6\times(-3)x^3y^2\\
&=\{4\times(-3)\}x^{4+3}y^{6+2}\\
&=-12x^7y^8
\end{align*}


単項式どうしの積はだいぶスラスラ求められるようになったよ!
単項式と多項式の積
多項式の積は、分配法則を使って計算します。
次の計算をせよ。
$~(1) 2x(x^3-4x+2)~$
$~(2) (2x^2-3xy+y^2)xy~$
(1)
\begin{align*}
2x(x^3-4x+2)&=2x\cdot x^3+2x\cdot(-4x)+2x\cdot2\\
&=2x^4-8x^2+4x\\
\end{align*}(2)
\begin{align*}
(2x^2-3xy+y^2)xy&=2x^2\cdot xy-3xy\cdot xy+y^2\cdot xy\\
&=2x^3y-3x^2y^2+xy^3\\
\end{align*}


上の例題で用いた$~\cdot~$は、積を表す記号で、$~\times~$と同じ意味だよ。
多項式どうしの積
多項式どうしの積も、分配法則を用いて計算します。
次の計算をせよ。
$~(3x^2-x-4)(x+2)~$
\begin{align*}
(3x^2-x-4)(x+2)&=(3x^2-x-4)x+(3x^2-x-4)\cdot2\\
&=3x^3-x^2-4x+6x^2-2x-8\\
&=3x^3+5x^2-6x-8
\end{align*}


同類項がたくさん出てきた。
これはこのまま降べきの順に並べればいいの?



同類項はしっかりとまとめておこう。
これ以上計算ができないようにしておくのが基本だよ!
最後は降べきの順に整理しようね。
このように、いくつかの多項式の積の形をした式について、その積を計算して単項式の和の形に表すことを、その式を「展開する」といいます。
1-2-C 展開の公式
交換法則、結合法則、分配法則からさまざまな形の展開の公式が得られます。
それらの公式は、式を展開するときによく使います。
次の展開の公式は既に中学校で学んだものです。
確認しておきましょう。
(1) $~(a+b)^2=a^2+2ab+b^2,(a-b)^2=a^2-2ab+b^2~$
(2) $~(a+b)(a-b)=a^2-b^2~$
(3) $~(x+a)(x+b)=x^2+(a+b)x+ab~$
中学校で習った展開の公式の復習
実際に例題を解いて復習してみましょう。
次の計算をせよ。
$~(1) (2x-4y)^2~$
$~(2) (3x+5y)(3x-5y)~$
$~(3) (x+6)(x-2)~$
(1)
\begin{align*}
(2x-4y)^2&=(2x)^2-2\cdot2x\cdot4y+(4y)^2\\
&=4x^2-16xy+16y^2\\
\end{align*}(2)
\begin{align*}
(3x+5y)(3x-5y)&=(3x)^2-(5y)^2\\
&=9x^2-25y^2\\
\end{align*}(3)
\begin{align*}
(x+6)(x-2)&=x^2+\{6+(-2)\}x+6\cdot(-2)\\
&=x^2+4x-12\\
\end{align*}


言われてみれば中学校で習った気がする!
すっかり忘れていたから、もう一度覚え直さなきゃ。
中学校で学んだ展開の公式を利用することによって、次の公式を求めることができます。
(4) $~(ax+b)(cx+d)=acx+(ad+bc)x+bd~$
展開の公式(4)を使った、式の展開
例題で確認してみましょう。
次の計算をせよ。
$~(1) (2x+3)(4x+5)~$
$~(2) (4x-y)(2x+6y)~$
(1)
\begin{align*}
(2x+3)(4x+5)&=2\cdot4x^2+(2\cdot5+3\cdot4)x+3\cdot5\\
&=8x^2+22x+15\\
\end{align*}(2)
\begin{align*}
(4x-y)(2x+6y)&=4\cdot2x^2+\{4\cdot6+(-1)\cdot2\}xy+(-1)\cdot6y^2\\
&=8x^2+22xy-6y^2\\
\end{align*}


途端に難しくなったよー。
助けて、ふくすけー。



数字や文字が増えても、本質は中学校で習った公式と同じだよ。
たくさん練習問題で計算して慣れよう!
1-2-D 式の計算の工夫
式の展開は、分配法則を使って計算することが基本です。
どうやって計算するか確認してみましょう。
次の計算をせよ。
$~(a+b+c)^2~$
\begin{align*}
(a+b+c)^2&=(a+b+c)(a+b+c)\\
&=(a+b+c)a+(a+b+c)b+(a+b+c)c\\
&=a^2+ab+ca+ab+b^2+cb+ac+bc+c^2\\
&=a^2+b^2+c^2+2ab+2bc+2ca
\end{align*}


もう限界だが?
数学、さらに嫌いになりそうだが?



確かに、こうやって展開してくのは大変だよね。
だから、式の計算に工夫を加えるんだ。
展開する式の形に応じて、ふさわしい工夫をしてから展開の公式を使うと、効率よく計算できる場合があります。
先ほどの$~(a+b+c)^2~$の展開では、$~a+b~$を1つのまとまりとみて、展開の公式を使って計算することもできます。
計算に工夫を加えた式の展開
実際に計算の工夫を加えたやり方をみてみましょう。
次の計算をせよ。
$~(a+b+c)^2~$
\begin{align*}
(a+b+c)^2&=\{(a+b)+c\}^2\\
&=(a+b)^2+2(a+b)c+c^2\\
&=a^2+2ab+b^2+2ac+2bc+c^2\\
&=a^2+b^2+c^2+2ab+2bc+2ca
\end{align*}$~a+b=A~$とおくと、$~(A+c)^2~$の展開になることがわかります。



おぉー。
登場する項の数が減って、計算が少しスッキリした気がするよ!



計算がスッキリすると、ミスが減るよ。
他にもさまざまな計算の工夫があるから、学んでいこう。
さまざまな計算の工夫
積の順序を変える、共通に出てくる式を1つにまとめるなどといった、計算の工夫を加えることで、展開の公式が使えるようになる場合があります。
次の計算をせよ。
$~(1) (a+2)^2(a-2)^2~$
$~(2) (x^2+xy+y^2)(x^2-xy+y^2)~$
(1)
\begin{align*}
(a+2)^2(a-2)^2&=\{(a+2)(a-2)\}^2\\
&=(a^2-4)^2\\
&=a^4-8a^2+16
\end{align*}(2)
\begin{align*}
(x^2+xy+y^2)(x^2-xy+y^2)&=\{(x^2+y^2)-xy\}\{(x^2+y^2)-xy\}\\
&=(x^2+y^2)^2-(xy)^2\\
&=x^4+2x^2y^2+y^4-x^2y^2\\
&=x^4+x^2y^2+y^4
\end{align*}


ただやみくもに計算するんじゃなくて、工夫を加えることで効率よく計算できるようになるね。



どういう計算の工夫をしたらいいかは、練習することですぐわかるようになるよ!
練習問題にチャレンジだ!
練習問題
今回の記事で解説した事項について、練習問題をまとめました。
練習問題を解くことで、今回の内容について理解を深めましょう。
大問1 多項式の和と差を求める計算
次の多項式$~A,B~$について、$~A+B~$と$~A-B~$を計算せよ。
$~(1) A=5x^3-2x^2-x+6,B=-4x^3+x^2-3x-8~$
$~(2) A=x^3-3+2x^2,B=-x^2+4x+3x^3-1~$
$~(3) A=7x^2+3xy-y^2,B=-2x^2+4xy-5y^2~$
大問1の解答と解説
(1) $~A+B=x^3-x^2-4x-2~$、$~A-B=9x^3-3x^2+2x+14~$
(2) $~A+B=4x^3+x^2+4x-4~$、$~A-B=-2x^3+3x^2-4x-2~$
(3) $~A+B=5x^2+7xy-6y^2~$、$~A-B=9x^2-xy+4y^2~$


大問2 文字による置き換え
$~A=x^2+2xy-y^2,B=-3x^2-3xy+2y,C=-2x^2+xy-3y^2~$であるとき、$~3(A-B)-(A+2B-C)~$を計算せよ。
大問2の解答と解説
$~15x^2+20xy-15y^2~$
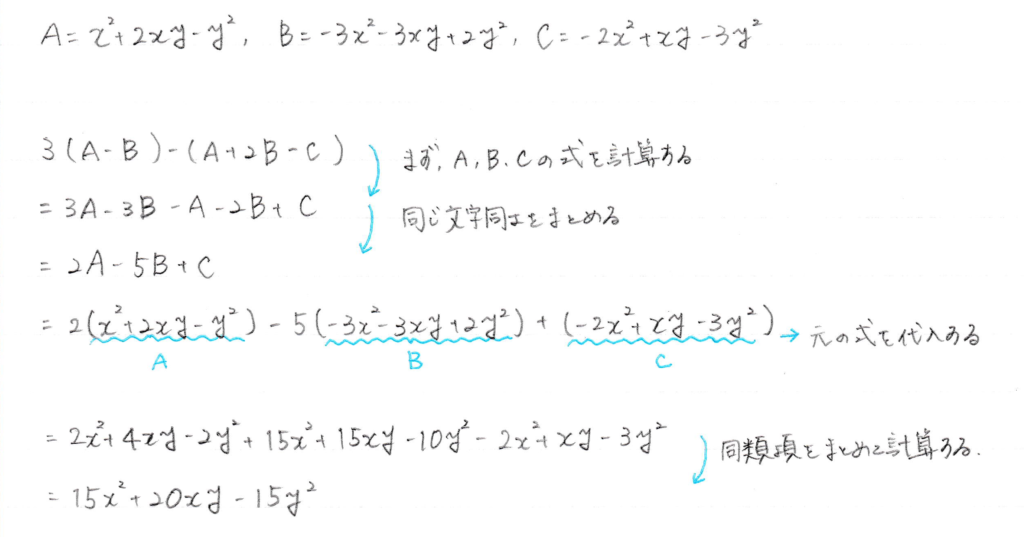
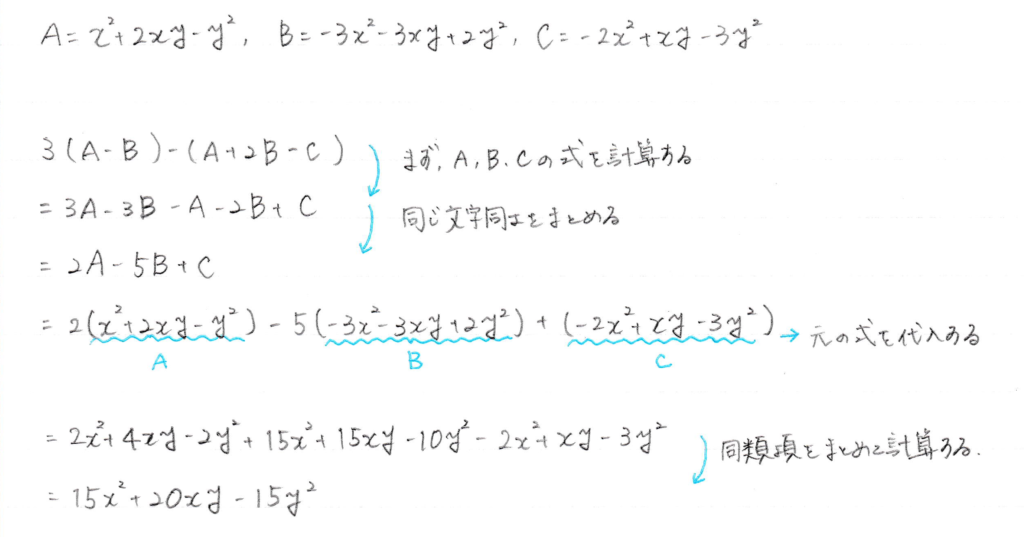
大問3 指数法則を用いた単項式の積
次の計算をせよ。
$~(1) 3x^2\times5x^3~$
$~(2) 2a^6b^2c\times(-4ab^3c^2)~$
$~(3) (2xy^2)^3\times(-3x^3y)^2~$
大問3の解答と解説
(1) $~15x^5~$
(2) $~-8a^7b^5c^3~$
(3) $~-72x^9y^8~$
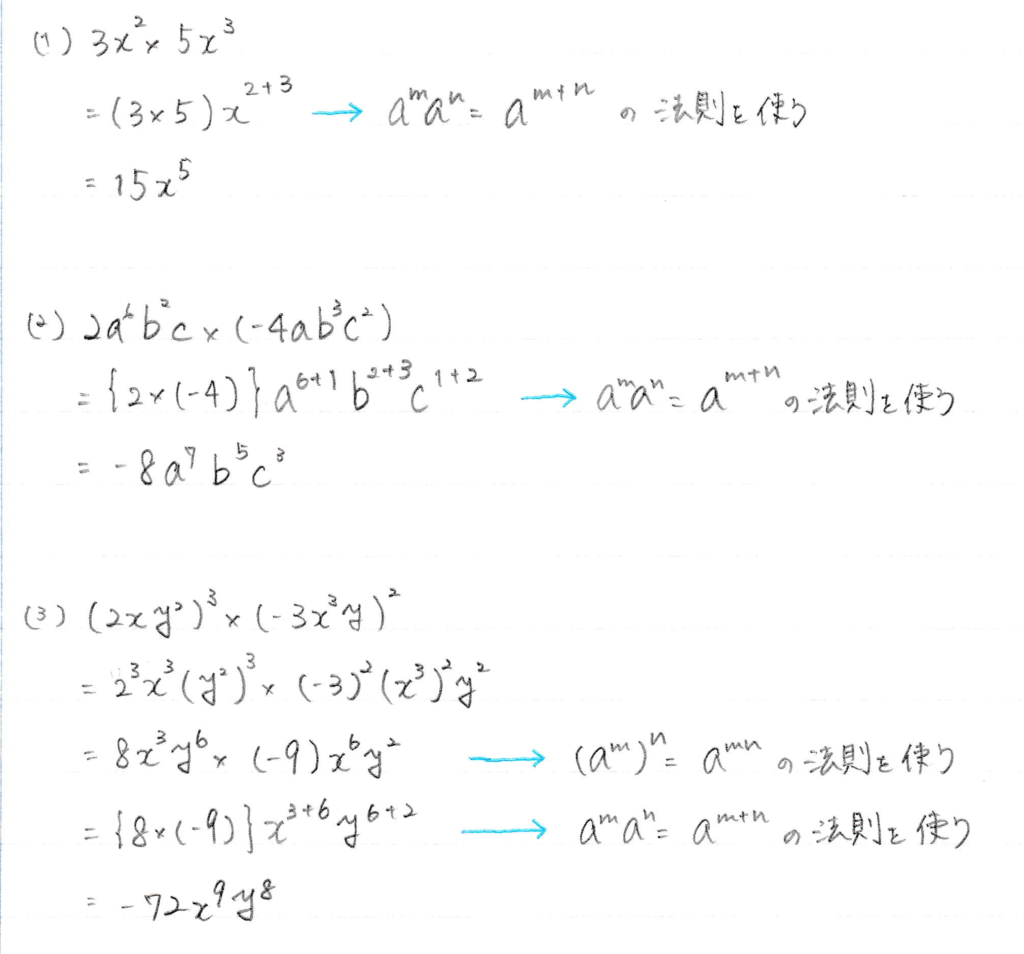
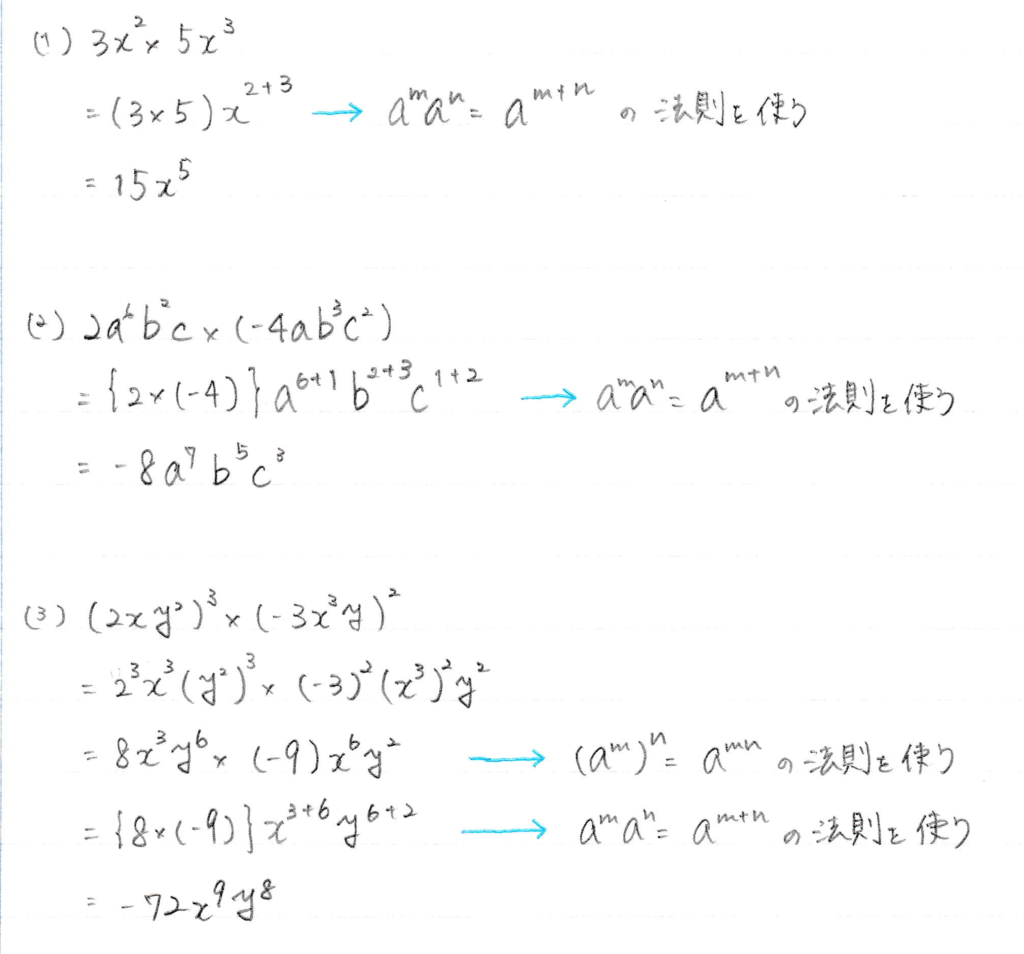
大問4 多項式の積
次の式を展開せよ。
$~(1) 2x^2(3x^2-4x+2)~$
$~(2) (2x^2-xy-y^2)(-3xy)~$
$~(3) (x^3+2x^2-3)(x-2)~$
$~(4) (x^3-2+3x^2)(3+x^2)~$
$~(5) (x+y)(x^2+2xy+y^2)~$
$~(6) (3x+2y+1)(x+y+2)~$
大問4の解答と解説
(1) $~6x^4-8x^3+4x^2~$
(2) $~-6x^3y+3x^2y^2+3xy^3~$
(3) $~x^4-4x^2-3x+6~$
(4) $~x^5+3x^4+3x^3+7x^2-6~$
(5) $~x^3+3x^2y+3xy^2+y^3~$
(6) $~3x^2+2y^2+5xy+7x+5y+2~$
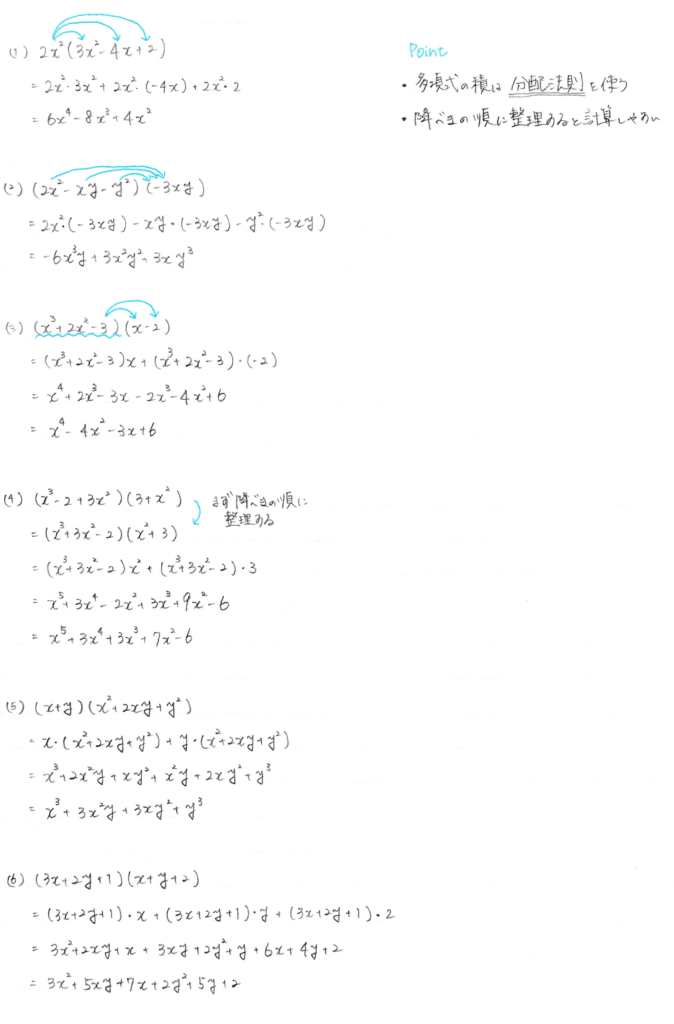
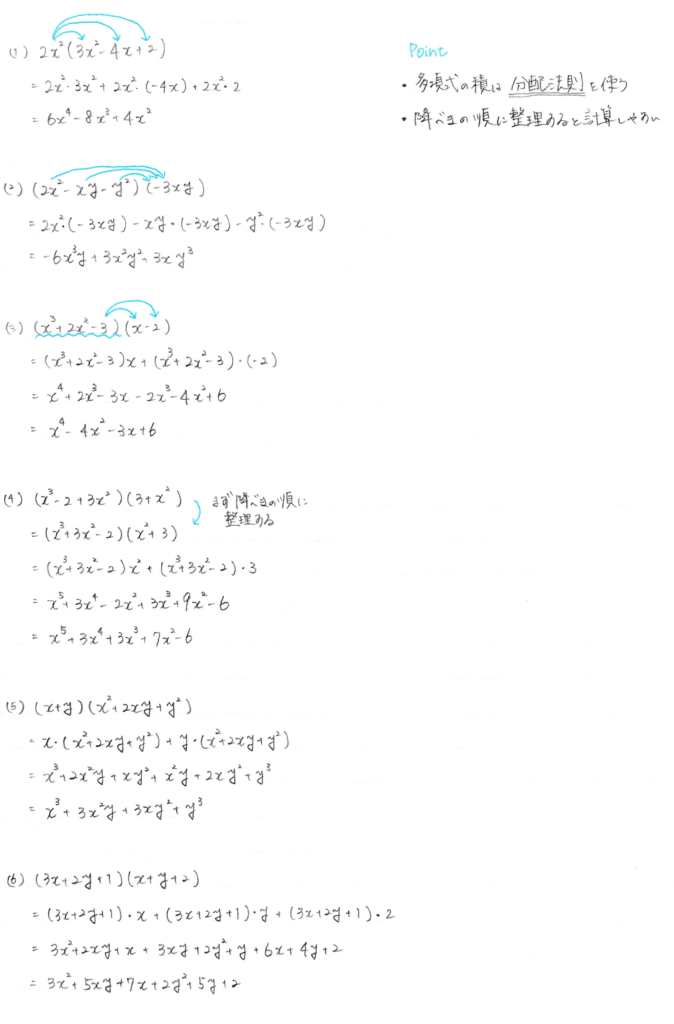
大問5 中学校までの展開の公式を使った計算
次の式を展開せよ。
$~(1) (2x+5)^2~$
$~(2) (2x-3y)^2~$
$~(3) (3x+4)(3x-4)~$
$~(4) (x+2)(x+6)~$
$~(5) (x-5)(x-2)~$
$~(6) (x-4y)(x+3y)~$
大問5の解答と解説
(1) $~4x^2+20x+25~$
(2) $~4x^2-12xy+9y^2~$
(3) $~9x^2-16~$
(4) $~x^2+8x+12~$
(5) $~x^2-7x+10~$
(6) $~x^2-xy-12y^2~$


大問6 展開の公式(4)を使った式の展開
次の式を展開せよ。
$~(1) (2x+4)(5x+3)~$
$~(2) (6x+2)(4x-7)~$
$~(3) (x-2y)(2x+3y)~$
$~(4) (4x-a)(3x-5a)~$
大問6の解答と解説
(1) $~10x^2+26x+12~$
(2) $~24x^2-34x-14~$
(3) $~2x^2-xy-6y^2~$
(4) $~12x^2-23ax+5a^2~$
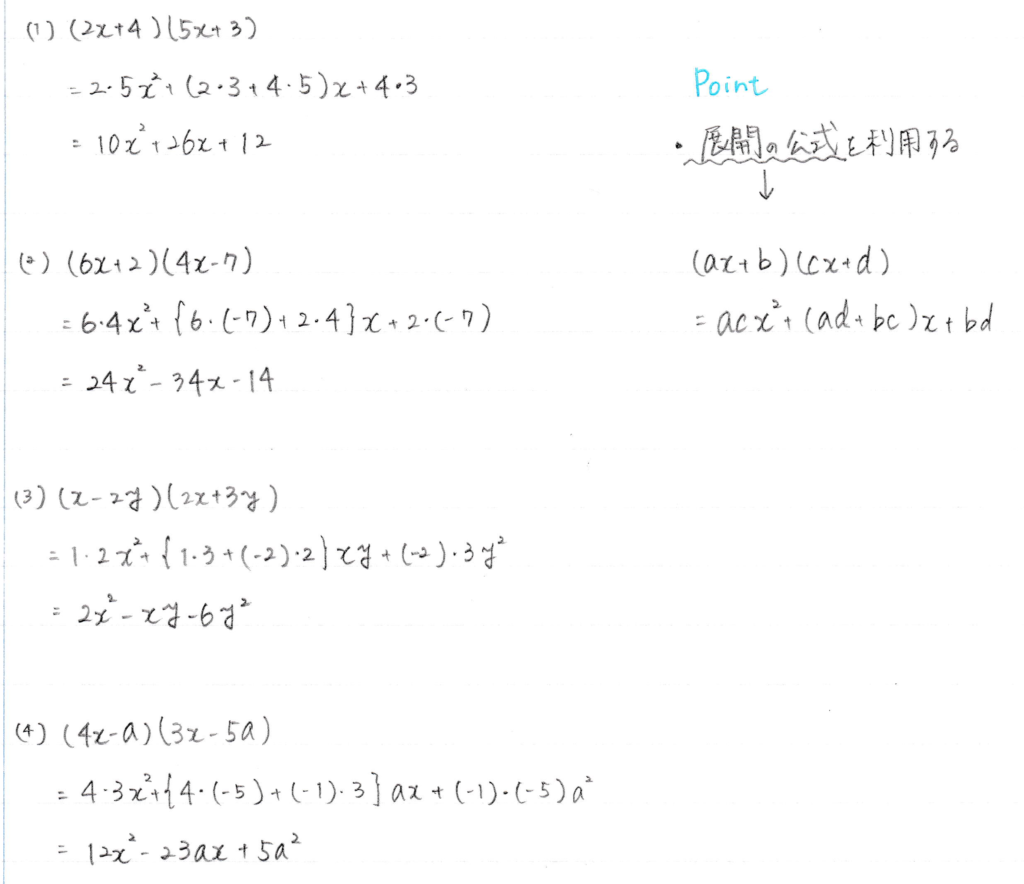
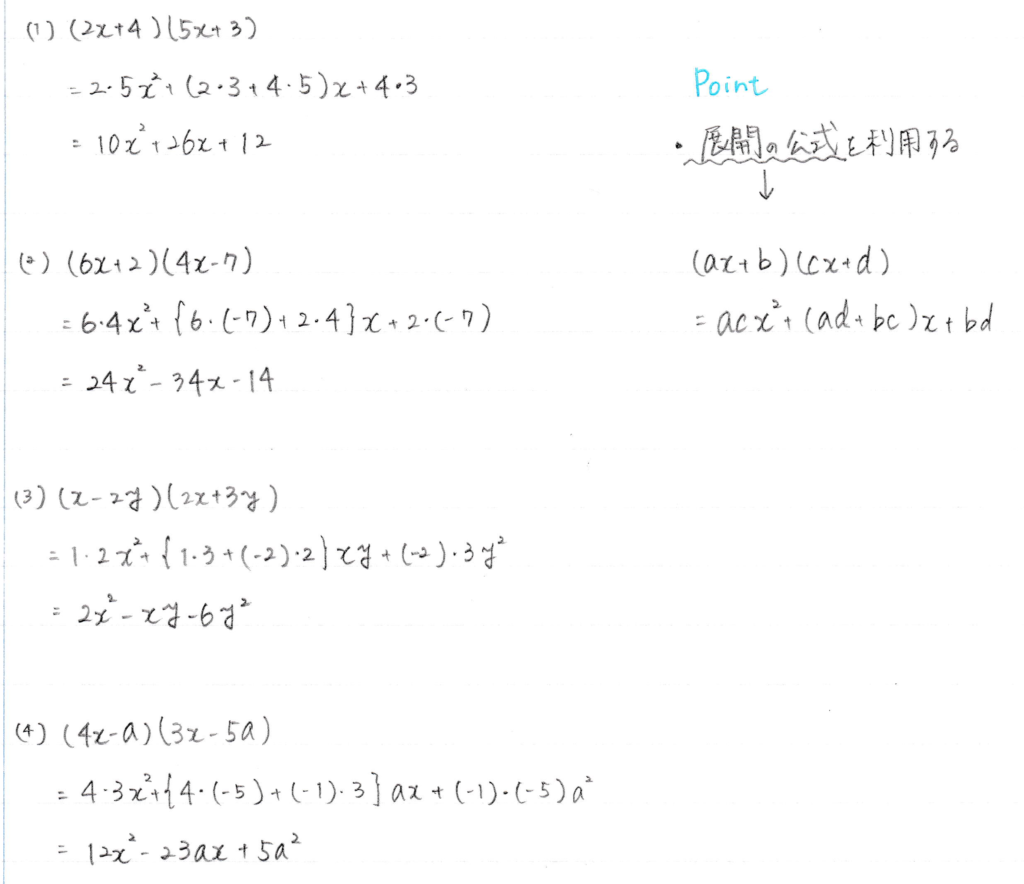
大問7 計算に工夫を加えた式の展開
次の式を展開せよ。
$~(1) (x+y-z)^2~$
$~(2) (a-3b+c)^2~$
大問7の解答と解説
(1) $~x^2+y^2+z^2+2xy-2yz-2zx~$
(2) $~a^2+9b^2+c^2-6ab-6bc+2ca~$


大問8 さまざまな計算の工夫
次の式を展開せよ。
$~(1) (x+y)^2(x-y)^2~$
$~(2) (a^2+4)(a+2)(a-2)~$
$~(3) (a^2+2a+5)(a^2-2a+5)~$
$~(4) (a-b+c)(a+b-c)~$
大問8の解答と解説
(1) $~x^4-2x^2y^2+y^4~$
(2) $~a^4-16~$
(3) $~a^4+6a^2+25~$
(4) $~a^2-b^2-c^2+2bc~$


まとめ
多項式どうしの積の計算も登場し、途中の計算が複雑になってきました。
そこで、計算の工夫を加え、少しでも計算が効率よくできるようになりましょう!

コメント