
$~\sin{x}~$が、$~\sin{z}~$だったら?
複素数の三角関数の定義や成り立つ公式、実数のときとの違いについて解説します。
- 複素数の三角関数の定義とその導出方法
- 実数の三角関数の公式が、複素数でも成り立つかどうか
- 実数の三角関数との相違点
Ⅰ 定義と導き方
複素数の三角関数は次のように定義されます。
$~z \in \mathbb{C}~$に対して、$~z~$の三角関数は次のように定義される。
\begin{align*}
\sin{z}&=\frac{e^{iz}-e^{-iz}}{2i} \\
\\
\cos{z}&=\frac{e^{iz}+e^{-iz}}{2} \\
\end{align*}三角関数を扱うつもりが、指数関数$~e^{iz}~,~e^{-iz}~$の登場・・・。
なぜ、指数関数が召喚されたかと言うと、オイラーの公式が関わっているからです。
定義ではありますが、その導き方を考えてみましょう。
実数$~\theta~$に対して、オイラーの公式
\begin{equation*}
e^{i \theta}=\cos{\theta}+i\sin{\theta} ~~~\cdots ①
\end{equation*}と、この$~\theta~$を$~-\theta~$とした場合の式
\begin{align*}
e^{i(-\theta)}&=\cos{(-\theta)}+i\sin{(-\theta)} \\
e^{-i\theta}&=\cos{\theta}-i\sin{\theta} ~~~~~~~\cdots ②
\end{align*}を考える。
$①-②~$によって、
\begin{align*}
e^{i \theta}-e^{-i \theta}&=2i \sin{\theta} \\
\\
\frac{e^{i \theta}-e^{-i \theta}}{2i}&=\sin{\theta} ~~~~\cdots ③
\end{align*}が求まり、同様に$~①+②~$によって、
\begin{align*}
e^{i \theta}+e^{-i \theta}&=2 \cos{\theta} \\
\\
\frac{e^{i \theta}+e^{-i \theta}}{2}&=\cos{\theta} ~~~~\cdots ④
\end{align*}が求まった。
$~③~,~④~$に$~\theta=z~$を代入することで、
\begin{equation*}
\sin{z}=\frac{e^{iz}-e^{-iz}}{2i}~~,~~\cos{z}=\frac{e^{iz}+e^{-iz}}{2}
\end{equation*}が定義された。■
ということで、オイラーの公式を使って導くということさえ覚えておけば、簡単に定義は導けそうです。
ちなみに、$~\tan{z}~$は、$~\sin{z}~,~\cos{z}~$から定義します。
\begin{align*}
\tan{z}&=\frac{\sin{z}}{\cos{z}}\\
\\
&=\frac{\dfrac{e^{iz}-e^{-iz}}{2i}}{\dfrac{e^{iz}+e^{-iz}}{2}} \\
\\
&=\frac{e^{iz}-e^{-iz}}{i(e^{iz}+e^{-iz})}
\end{align*}これで$~\sin{z}~,~\cos{z}~,~\tan{z}~$が揃いましたが、実数のときとは全く違った形になってしまいました。
Ⅱ 三角関数の公式
三角関数を定義したいはずが、$~e~$まで登場し、
「これはもはや三角関数と別物では?」
という疑問の声も出てくるはずです。
そこで、実数$~\theta~$のときに成り立っていた次のような性質が、複素数$~z~$でも成り立つのかを確かめてみましょう。
- $~\sin^2{z}+\cos^2{z}=1~$
- $~\sin{(-z)}=-\sin{z}~$
- $~\sin{(z_1+z_2)}=\sin{z_1}\cos{z_2}+\cos{z_1}\sin{z_2}~$
- $~\sin{(z+2n \pi)}=\sin{z}~$
- $~e^{iz}=\cos{z}+i\sin{z}~$
上の5つの性質は、単に定義を代入することで、証明することが可能です。
- 左辺に定義を代入する。
\begin{align*}
&~~~\sin^2{z}+\cos^2{z} \\
\\
&=\left( \frac{e^{iz}-e^{-iz}}{2i} \right)^2+\left( \frac{e^{iz}+e^{-iz}}{2} \right)^2 \\
\\
&=\frac{e^{2iz}-2+e^{-2iz}}{-4}+\frac{e^{2iz}+2+e^{-2iz}}{4} \\
\\
&=\frac{-e^{2iz}+2-e^{-2iz}+e^{2iz}+2+e^{-2iz}}{4} \\
\\
&=\frac{4}{4} \\
\\
&=1 ~~~~~~~~\blacksquare
\end{align*}- 左辺に定義を代入する。
\begin{align*}
\sin{(-z)}&=\frac{e^{-iz}-e^{iz}}{2i} \\
\\
&=\frac{-e^{iz}+e^{-iz}}{2i} \\
\\
&=-\frac{e^{iz}-e^{-iz}}{2i} \\
\\
&=-\sin{z} ~~~~~~~~\blacksquare
\end{align*}- 右辺に定義を代入し、左辺を導く。
\begin{align*}
&~~~\sin{z_1}\cos{z_2}+\cos{z_1}\sin{z_2} \\
\\
&=\left( \frac{e^{iz_1}-e^{-iz_1}}{2i} \right) \left( \frac{e^{iz_2}+e^{-iz_2}}{2} \right)+\left( \frac{e^{iz_1}+e^{-iz_1}}{2} \right) \left( \frac{e^{iz_2}-e^{-iz_2}}{2i} \right) \\
\\
&=\frac{e^{i(z_1+z_2)}+e^{i(z_1-z_2)}-e^{-i(z_1-z_2)}-e^{i(z_1+z_2)}}{4i}\\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+\frac{e^{i(z_1+z_2)}-e^{i(z_1-z_2)}+e^{-i(z_1-z_2)}-e^{i(z_1+z_2)}}{4i} \\
\\
&=\frac{2e^{i(z_1+z_2)}-2e^{-i(z_1+z_2)}}{4i} \\
\\
&=\frac{e^{i(z_1+z_2)}-e^{-i(z_1+z_2)}}{2i} \\
\\
&=\sin{(z_1+z_2)} ~~~~~~~~\blacksquare
\end{align*}- 左辺に定義を代入すると、
\begin{align*}
&~~~\sin{(z+2n \pi)} \\
\\
&=\frac{e^{i(z+2n \pi)}-e^{-i(z+2n \pi)}}{2i} \\
\\
&=\frac{e^{iz}\cdot e^{2n \pi i}-e^{-iz}\cdot e^{-2n \pi i}}{2i} ~~~\cdots ⑤
\end{align*}であり、ここでオイラーの公式より、
\begin{align*}
e^{2n \pi i}&=\cos{(2n\pi)}+i \sin{(2n \pi)} \\
&=1 \\
\\
e^{-2n \pi i}&=\cos{(-2n\pi)}+i \sin{(-2n \pi)} \\
&=\cos{(2n\pi)}-i \sin{(2n \pi)} \\
&=1 \\
\end{align*}なので、これらを$⑤$に代入すると、
\begin{align*}
&~~~\frac{e^{iz}\cdot 1-e^{-iz}\cdot 1}{2i} \\
\\
&=\frac{e^{iz}-e^{-iz}}{2i} \\
\\
&=\sin{z}
\end{align*}が求まる。■
- 右辺に定義を代入し、左辺を導く。
\begin{align*}
&~~~\cos{z}+i \sin{z} \\
\\
&=\frac{e^{iz}+e^{-iz}}{2}+i\frac{e^{iz}-e^{-iz}}{2i} \\
\\
&=\frac{e^{iz}+e^{-iz}+e^{iz}-e^{-iz}}{2} \\
\\
&=\frac{2e^{iz}}{2} \\
\\
&=e^{iz} ~~~~~~~~\blacksquare
\end{align*}実数で使っていた三角関数の公式が、複素数の定義でも正しいことが確かめられました。
もちろん、他にも三角関数の公式は存在しますが、同様の方法で正しいことが確かめられます。
Ⅲ 実数の三角関数との相違点
実数のときには当然のように扱っていた性質の中で、複素数の場合は成り立たない性質が1つあります。
$~z \in \mathbb{C}~$に対して、
\begin{equation*}
|\sin{z}| \leq 1 ~~~~,~~~~|\cos{z}| \leq 1
\end{equation*}は必ずしも成立しない。
実数の場合、単位円からもわかるように、当たり前のように成り立っていた性質です。
複素数$~z=x+iy~$の絶対値が
\begin{equation*}
|z|=\sqrt{x^2+y^2}
\end{equation*}と定義されることを踏まえた上で、いくつか反例を示しましょう。
\begin{align*}
|\sin{i}|&=\left| \frac{e^{-1}-e^{1}}{2i} \right| \\
\\
&=\left| \frac{e^{-1}-e^{1}}{-2}i \right| \\
\\
&=\left| \frac{1}{2}\left( -\frac{1}{e}+e \right) i \right| \\
\\
&=\sqrt{ \left\{ \frac{1}{2}\left( e-\frac{1}{e} \right) \right\}^2 } \\
\\
&=\frac{1}{2}\left( e-\frac{1}{e} \right)
\end{align*}この式を近似計算すると、$~1.175 \cdots ~$となり、$~|\sin{z}| \leq 1~$は成り立たない。
\begin{align*}
|\cos{(\pi-i)}|&=\left| \frac{e^{i(\pi -i)}+e^{-i(\pi-i)}}{2} \right| \\
\\
&=\left| \frac{e^{i\pi+1}+e^{-i\pi-1}}{2} \right| \\
\\
&=\left| \frac{e^{i\pi}\cdot e^1+e^{-i\pi}\cdot \frac{1}{e}}{2} \right| \\
\\
&=\left| \frac{-1\cdot e-1\cdot \frac{1}{e}}{2} \right| \\
\\
&=\left| \frac{1}{2} \left(-e-\frac{1}{e}\right) \right| \\
\\
&=\sqrt{ \left\{ \frac{1}{2} \left(-e-\frac{1}{e}\right) \right\}^2 } \\
\\
&=\frac{1}{2} \left(e+\frac{1}{e}\right)
\end{align*}$~e > 2 ~$より、$~|\sin{z}| \leq 1~$は成り立たない。
反例2では、ネイピア数$~e \fallingdotseq 2.718~$より、明らかに$~1~$を超えてしまうことがわかりますね。
実数との違い、覚えておきましょう。





三角比ってもともとは直角三角形の辺の比なのに・・・。



数学の力ってすごいよね。
無茶苦茶なことをしているようで、論理的には正しいことをしているんだもん。
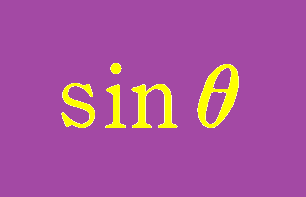
コメント