基礎例題と問題解説で数学Ⅰを教科書の流れで理解する「れいもん」。
今回は因数分解についての用語や因数分解の仕方についてを理解しましょう。
- 因数分解と因数について
- 因数分解の公式
- 式の特徴に着目して工夫をした因数分解
「れいもん」では、数研出版の検定済教科書『数学Ⅰ』の流れに沿って、例題と問題を解説しています。
手書きの解説は、タップすることで拡大することができます。
1-3-A 共通な因数をくくり出す
まず、因数分解についての用語を理解しましょう。
- 因数分解‥‥1つの多項式を、1次以上の多項式の積の形に表すこと。例:$~x^2-x-2=(x-2)(x+1)~$
- 因数‥‥積を作っている各式。

因数分解かぁ……。
難しそう。



因数分解は数Ⅰの最初の大きな山だよ。
気を引き締めていこう。
式を因数分解するとき、まず、各項に共通な因数があれば、
AB+AC=A(B+C)
と、その共通因数を括弧の外にくくり出します。
共通な因数のくくり出し
実際にどう共通因数をくくり出すのか、例題で確認してみましょう。
次の式を因数分解せよ。
$~(1) 12x^2y^2-8xy^3~$
$~(2) (x-y)a+(y-x)b~$
(1)
\begin{align*}
12x^2y^2-8xy^3&=4xy^2\cdot3x-4xy^2\cdot2y\\
&=4xy^2(3x-2y)\\
\end{align*}(2)
\begin{align*}
(x-y)a+(y-x)b&=(x-y)a-(x-y)b\\
&=(x-y)(a-b)\\
\end{align*}


各項に共通する数や文字を見つければいいんだね!
1-3-B 因数分解の公式
「れいもん」1-1-2で学んだ、展開の公式を逆にして見てみましょう。



あ、さっきの因数分解の例に似てる。



いいところに気が付いたね!
そうです、展開の公式を逆にみることで、因数分解の公式が得られます。
次の因数分解の公式1~3は、中学校で学んだものです。
復習のつもりで確認しましょう。
(1) $~a^2+2ab+b^2=(a+b)^2,a^2-2ab+b^2=(a-b)^2~$
(2) $~a^2-b^2=(a+b)(a-b)~$
(3) $~x^2+(a+b)x+ab=(x+a)(x+b)~$



中学校でこんなに教わったっけ?
覚えてないなぁ……。



そんなねこさまのために例題を用意したから、次の項でたくさん復習しよう!
中学校で学ぶ因数分解の公式を利用した計算
次の式を因数分解せよ。
$~(1) x^2+6x+9~$
$~(2) 4a^2-20ab+25b^2~$
$~(3) 16x^2-9y^2~$
$~(4) x^2+6x+8~$
$~(5) x^2-xy-12y^2~$
(1)
\begin{align*}
&~~~~~x^2+6x+9\\
&=x^2+2\cdot x\cdot 3+3^2\\
&=(x+3)^2\\
\end{align*}(2)
\begin{align*}
&~~~~~4a^2-20ab+25b^2\\
&=(2a)^2-2\cdot 2a\cdot 5b+(5b)^2\\
&=(2a-5b)^2\\
\end{align*}(3)
\begin{align*}
&~~~~~16x^2-9y^2\\
&=(4x)^2-(3y)^2\\
&=(4x+3y)(4x-3y)\\
\end{align*}(4)
\begin{align*}
&~~~~~x^2+6x+8\\
&=x^2+(4+2)x+4\cdot2\\
&=(x+4)(x+2)\\
\end{align*}(5)
\begin{align*}
&~~~~~x^2-xy-12y^2\\
&=x^2+(-4y+3y)x+(-4y)\cdot3y\\
&=(x-4y)(x+3y)\\
\end{align*}数学Ⅰで学ぶ展開の公式を利用した計算
数学Ⅰでは、中学校で学んだ展開の公式に加え、新たにもう1つ展開の公式を学びます。
(4) $~acx^2+(ad+bc)x+bd=(ax+b)(cx+d)~$



いきなり難易度高くない?
暗号文じゃない?
イメージしやすくするために、具体例で確認してみましょう。
$~3x^2+8x+5~$を因数分解せよ。
公式$~acx^2+(ad+bc)x+bd=(ax+b)(cx+d)~$において、$~ac=3,ad+bc=8,bd=5~$となる$~a,b,c,d~$を見つける。
$~a=1,c=3~$とすると、$~bd=5~$となるのは次の場合である。
$~(b,d)=(1,5), (b,d)=(5,1), (b,d)=(-1,-5), (b,d)=(-5,-1)~$
これらの中で、$~ad+bc=8~$となるのは、$~b=1,d=5~$のときである。
よって $~3x^2+8x+5=(x+1)(3x+5)~$
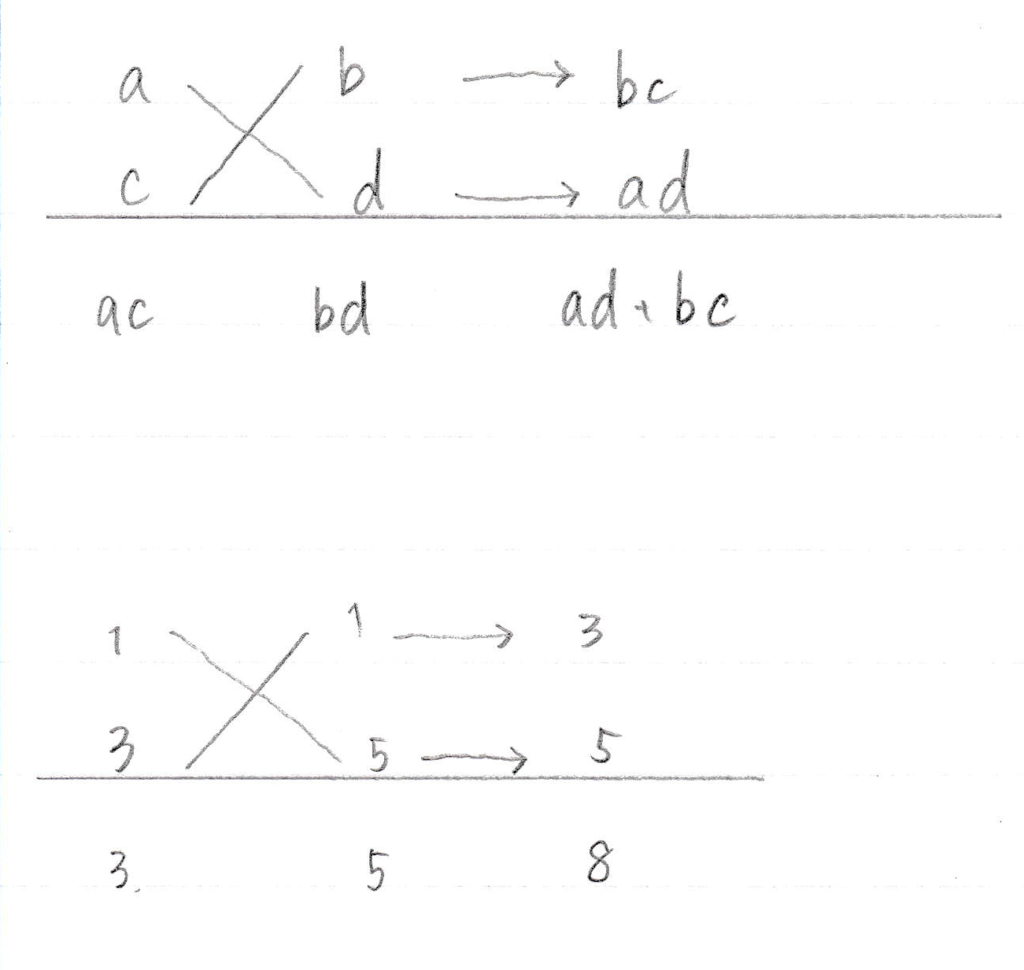

※例題3で使った計算方法をたすき掛けといいます。



たすき掛け、慣れてきたら便利なツールかもしれない!



例題3の解説みたいに、一つ一つ場合分けしなくていいから、ぜひ覚えてほしい計算方法だよ!
たすき掛けを使った因数分解
では、実際にたすき掛けを使った因数分解の練習をしてみましょう。
次の式を因数分解せよ。
$~(1) 4x^2-4x-15~$
$~(2) 4x^2-2xy-y^2~$
(1)
4x^2-4x-15=(2x-5)(2x+3)
(2)
4x^2-2xy-y^2=(x-y)(4x+2y)



たすき掛け、慣れてきた気がする!
難しそうにみえた因数分解が、私にもできるって思えた!
1-3-C 式の特徴に着目した工夫
式を因数分解するとき、式の特徴に着目して式の変形をすると、因数分解の公式が利用できるようになることがあります。



一見、因数分解できなさそうな多項式も因数分解できるってこと?
えー、因数分解、やっぱり面倒くさいなぁ……。



まぁまぁ、ねこさま、そう言わないで。
ほんの少しの工夫で、すぐ因数分解の公式が使えるってわかるようになるから!
次の式を因数分解せよ。
x^2-y^2+8y-16
\begin{align*}
x^2-y^2+8y-16&=x^2-(y^2-8y+16)\\
&=x^2-(y-4)^2\\
&=\{x+(y-4)\}\{x-(y-4)\}\\
&=(x+y-4)(x-y+4)
\end{align*}このように、与えられた式を変形して、平方の差$~X^2-Y^2~$の形を作ると、因数分解の公式(2)が利用できます。
平方の差を利用した因数分解
平方の差を利用した因数分解の例題をみてみましょう。
次の式を因数分解せよ。
x^4-9x^2+20
\begin{align*}
&~~~~~x^4-9x^2+20\\
&=(x^2)^2-9x^2+20\\
&=(x^2-5)(x^2-4)\\
&=(x^2-5)(x+2)(x-2)
\end{align*}


$~x^2~$を$~A~$とおくと、
$~A^2-9A+20=(A-5)(A-4)~$となって、因数分解が簡単になるね。
2種類以上の文字を含む式の因数分解
2種類以上の文字を含む式は、最も次数の低い文字に着目して降べきの順に整理すると、効率よく因数分解できることがあります。
次の式を因数分解せよ。
x^3+x^2y+2x^2-4y
\begin{align*}
&~~~~~x^3+x^2y+2x^2-4y\\
&=(x^2-4)y+(x^3+2x^2)\\
&=(x+2)(x-2)y+x^2(x+2)\\
&=(x+2)\{(x-2)y+x^2\}\\
&=(x+2)(x^2+xy-2y)\\
\end{align*}この例題は$~x~$については3次式、$~y~$については1次式なので、次数の低い$~y~$について降べきの順に整理しました。



無理だぁ……。
これは暗号だよ。
公式が使えるかパッと見て分からないもん……。



とにかく、一番次数の低い文字を探そう!
そして、降べきの順に整理してみて考えよう!
2種類以上の文字を含む式の因数分解 ~続き~



だんだん因数分解も複雑になってきて、ねこさまも苦戦しているね。
例題や、最後に載せる練習問題で練習して、因数分解を得意にしよう。



そんなに問題解きたくない……。
次の式を因数分解せよ。
2x^2-5xy-3y^2+5x-y+2
\begin{align*}
&~~~~~2x^2-5xy-3y^2+5x-y+2\\
&=2x^2+(-5y+5)x-(3y^2+y-2)\\
&=2x^2+(-5y+5)x-(3y-2)(y+1)\\
&=\{2x-(3y-2)\}\{x+(y+1)\}\\
&=(2x-3y+2)(x+y+1)\\
\end{align*}例題8の式は、$~x~$についても、$~y~$についての2次式でした。
どちらで降べきの順に整理してもいいのですが、ここでは$~x~$について降べきの順に整理しました。



多項式でも、たすき掛けは使えるんだね。



複雑に見える式でも、まず次数の低い文字に着目して降べきの順に整理することを覚えておこう!
対称式
ここまでさまざまな式を計算してきた因数分解の解説も最後の章になりました。
最後も、次数の低い文字に着目して降べきの順に整理するという方法は変わりません。
次の式を因数分解せよ。
ab(a-b)+bc(b-c)+ca(c-a)
\begin{align*}
&~~~~~ab(a-b)+bc(b-c)+ca(c-a)\\
&=a^2b-ab^2+b^2c-bc^2+c^2a-ca^2\\
&=(b-c)a^2-(b^2-c^2)a+b^2c-bc^2\\
&=(b-c)a^2-(b+c)(b-c)a+bc(b-c)\\
&=(b-c)\{a^2-(b+c)a+bc\}\\
&=(b-c)(a-b)(a-c)\\
&=-(a-b)(b-c)(c-a)
\end{align*}


この問題に関しては、最後の答えが、$~(b-c)(a-b)(a-c)~$まででもOKだよ。



元の式はとても簡単そうだったけど、共通因数をくくり出して、たすき掛けを使って、平方の差を利用して……、今まで習ったことが全部出てきているね。



それだけ因数分解は覚える式や計算方法がたくさんあるんだ。
でも、味方につけてしまえばどんな問題でもスラスラ解けるよ!
練習問題
大問1 共通な因数のくくり出し
次の式を因数分解せよ。
$~(1) 2x^2y-10xy^2+14xyz~$
$~(2) 3x^2yz-2x^2yz^2+xyz~$
$~(3) x(a-b)-ay+by~$
$~(4) x(5y-2)+3(5y-2)~$
大問1の解答と解説
$~(1) 2xy(x-5y+7)~$
$~(2) xyz(3x-2xz+1)~$
$~(3) (a-b)(x-y)~$
$~(4) (5y-2)(x-3)~$


大問2 中学校で学ぶ因数分解の公式を利用した計算
次の式を因数分解せよ。
$~(1) x^2-10x+25~$
$~(2) 9x^2+42xy+49y~$
$~(3) 4a^2-46ab+81b^2~$
$~(4) 9x^2-25y^2~$
$~(5) x^2+8x+12~$
$~(6) x^2-6xy+8y^2~$
$~(7) x^2+xy-20y^2~$
$~(8) x^2-2ax-35a^2~$
大問2の解答と解説
$~(1) (x-5)^2~$
$~(2) (3x+7y)^2~$
$~(3) (2a-9b)^2~$
$~(4) (3x+5y)(3x-5y)~$
$~(5) (x+2)(x+6)~$
$~(6) (x-4y)(x-2y)~$
$~(7) (x+5y)(x-4y)~$
$~(8) (x-7a)(x+5a)~$


大問3 たすき掛けを使った因数分解
次の式を因数分解せよ。
$~(1) 2x^2-x-1~$
$~(2) 2x^2-11x+15~$
$~(3) 6x^2-x-12~$
$~(4) 3a^2-2ab-b^2~$
$~(5) 3a^2-17ab+10b^2~$
$~(6) 4a^2-8ab-21b^2~$
大問3の解答と解説
$~(1) (2x+1)(x-1)~$
$~(2) (2x-5)(x-3)~$
$~(3) (3x+4)(2x-3)~$
$~(4) (3a+b)(a-b)~$
$~(5) (3a-2b)(a-5b)~$
$~(6) (2a+3b)(2a-7b)~$
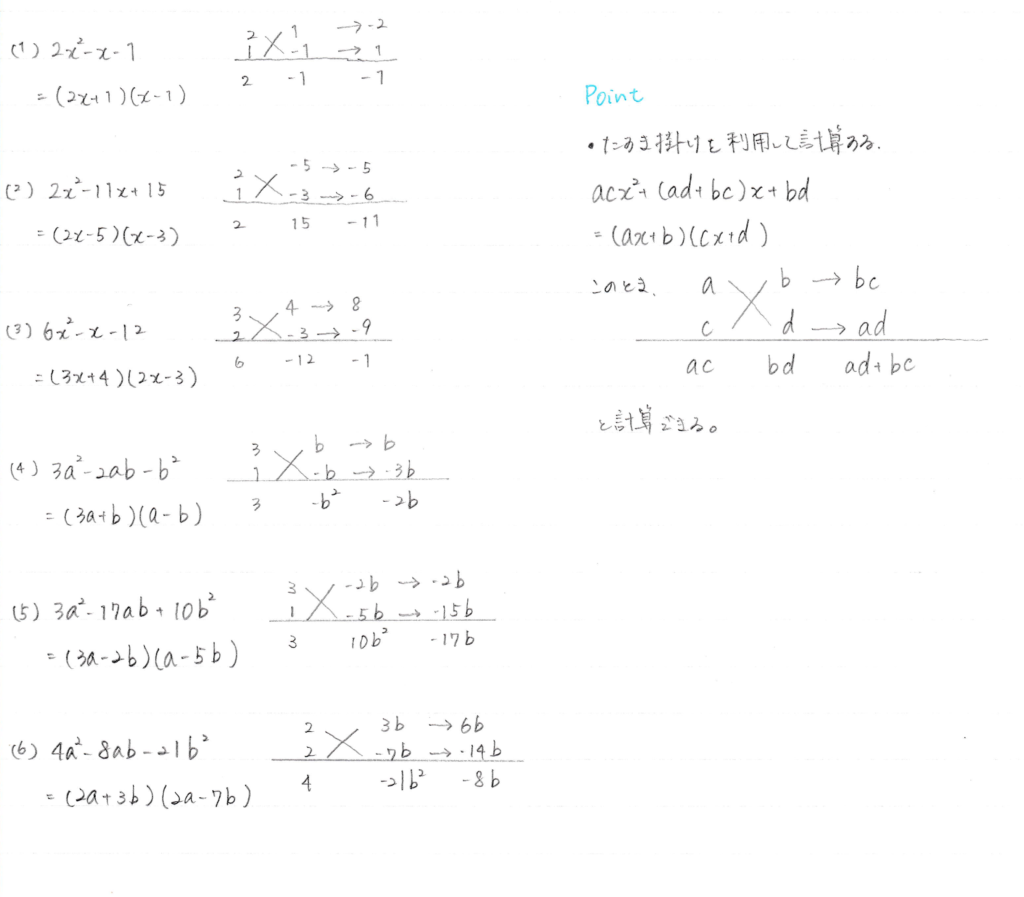
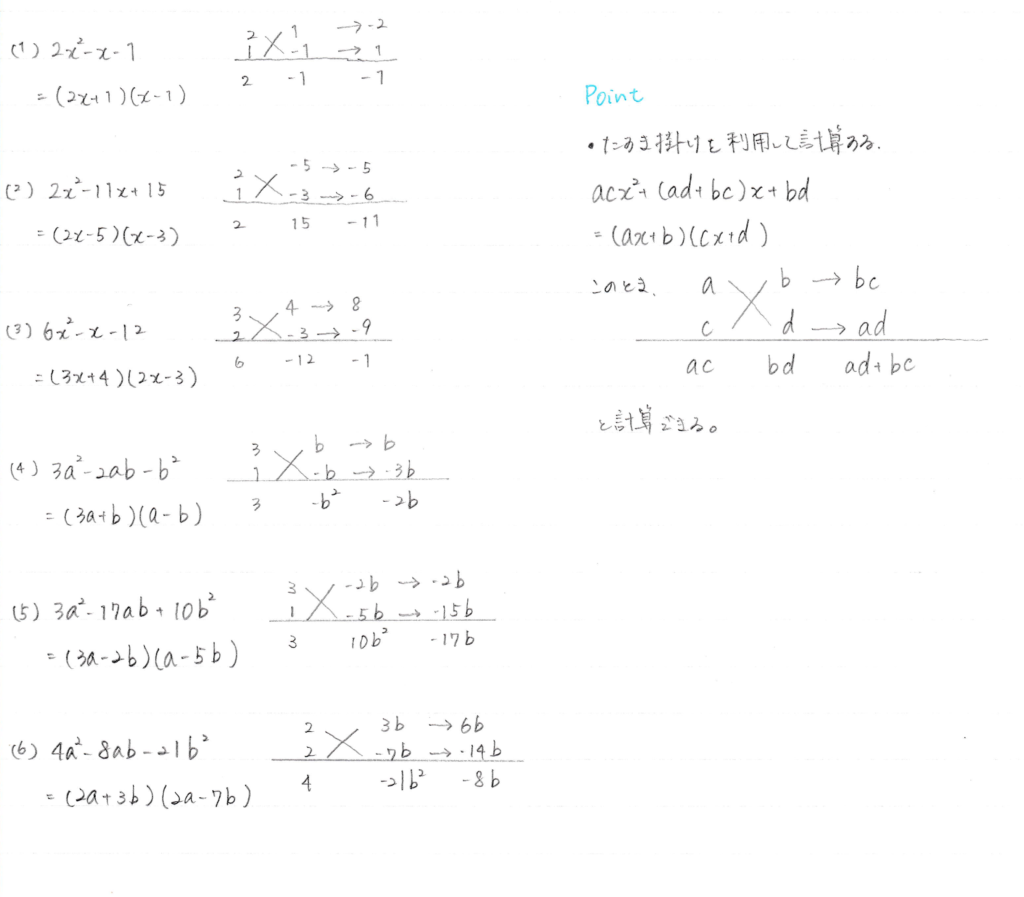
大問4 平方の差を利用した因数分解
次の式を因数分解せよ。
$~(1) x^2-y^2-4y-4~$
$~(2) x^2-8x+16-36y^2~$
大問4の解答と解説
$~(1) (x+y+2)(x-y-2)~$
$~(2) (x+6y-4)(x-6y-4)~$


大問5 式の特徴に着目し工夫をした因数分解
次の式を因数分解せよ。
$~(1) x^4-10x^2+9~$
$~(2) x^4-16~$
$~(3) (x^2+5x)^2-2(x^2+5x)-24~$
大問5の解答と解説
$~(1) (x+3)(x-3)(x+1)(x-1)~$
$~(2) (x^2+4)(x+2)(x-2)~$
$~(3) (x+4)(x+1)(x+6)(x-1)~$


大問6 2種類以上の文字を含む式の因数分解
次の式を因数分解せよ。
$~(1) x^2-2yz+zx-4y^2~$
$~(2) 8b-16-2ab+a^2~$
$~(3) 2x^2-8xy-5x-4y-3~$
大問6の解答と解説
$~(1) (x-2y)(x+2y+z)~$
$~(2) (a-4)(a-2b+4)~$
$~(3) (2x+1)(x-4y-3)~$


大問7 2種類以上の文字を含む式の因数分解 ~続き~
次の式を因数分解せよ。
$~(1) x^2+5xy+6y^2+x+y-2~$
$~(2) 3x^2+5xy-2y^2+2x+11y-5~$
大問7の解答と解説
$~(1) (x+3y+2)(x+2y-1)~$
$~(2) (3x-y+5)(x+2y-1)~$


大問8 対称式
次の式を因数分解せよ。
$~a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)~$
大問8の解答と解説
$~(a-b)(b-c)(c-a)~$


まとめ
数Ⅰの最初の大きな山の一つである、因数分解。
覚えなければならない用語や、計算方法がたくさんあって戸惑う人も多いでしょう。
しかし、一度、用語や計算方法をマスターしてしまえば、この先の数学の計算でも心強い味方になってくれます。
例題と練習問題で着実にマスターしましょう!

コメント