
中学校1年生で習う「一次方程式」の応用問題として、授業で使える教材です。
パズル的な要素が強く、深く追究すると不定解や不能解の話まで登場するため、幅広い学力層で有効な数学的活動となっています。
- 「数の鎖」という教材について
- 「数の鎖」の主題とタネ明かし
- 不定解や不能解となる「数の鎖」
Ⅰ 数の鎖とは?
Ⅰー① 教材のネタ元
この記事で紹介する「数の鎖」は、『思考力・表現力がぐんぐん伸びる!数学レポート実践集』という書籍に載っている教材です。
「数の鎖」を題材に、研究授業を何度か行い、その中で見えてきた自分なりの反省点や生徒の反応について、まとめておきます。
Ⅰー② 対象学年・単元
パズルのような教材なので、小学生でも十分に楽しめます。
実際、小学生に授業をしたときも評判は良かったです。
しかし、教材としての効果が一番高い対象学年は、中学1年生。
公立・私立の偏差地帯問わず、扱うことができます。
そして、対称単元は方程式です。
一次方程式の計算はできる前提で、応用問題の一環として使用するのが最適です。
Ⅱ 数の鎖のルール(導入部)
まずは、数の鎖のルールを生徒全員に定着させるために、時間を使います。
Ⅱー① 数の鎖のルール
数の鎖とは、以下のようなルールで数がつながったものを言います。
数の鎖とは、丸と四角を交互に繋げたもので、四角の中には両隣の丸の和が入る。
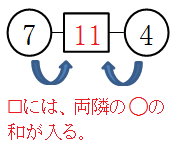

ルール自体は単純で、中学生は全員が理解できました。
小学生に対しては、いまいちピンと来ていない児童も過去数人いましたが、次の問題を解くことで解決します。
Ⅱー② 数の鎖の例題
数の鎖のルールを確実に定着させるため、次のような問題をまず解きます。
次の数の鎖を完成させなさい。
例題1


例題2
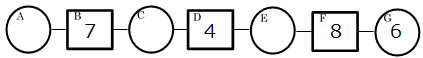
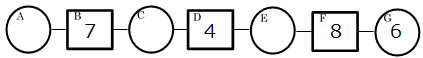
右からひき算をするだけなので、簡単に解けます。
例題1の解答
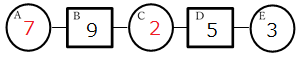
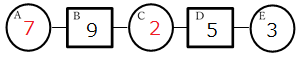
$~C+E=D~$より、$~C=D-E=5-3=2~$
$~A+C=B~$より、$~A=B-C=9-2=7~$
例題2の解答
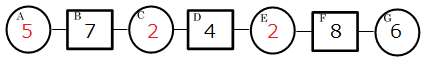
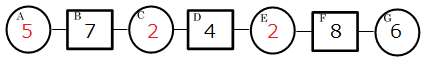
$~E+G=F~$より、$~E=G-F=8-6=2~$
$~C+E=D~$より、$~C=D-E=4-2=2~$
$~A+C=B~$より、$~A=B-C=7-2=5~$
この2問の例題を通して、小学生を含めて誰もがルールを理解し、定着させることができました。
生徒に好きな自然数を言ってもらい、その場で$~B~,~D~,~F~$を埋めて作問すると、生徒目線の題材となり、その後の展開がスムーズです。
その場合、右端だけは教員が埋めましょう。(小学生の場合、負の数が出てしまうと計算できないため)
Ⅲ 数の鎖の主題(展開部)
例題は引き算で解決できるため、生徒に方程式の良さを実感させることはできません。
あくまでも、「数の鎖」のルールを定着させることが目的でした。
Ⅲー① 数の鎖の主題
ルールを定着させた後は次の問題を出題し、この教材の本質へと迫っていきます。
次の数の鎖の両端には同じ数が入る。このとき、数の鎖を完成させなさい。
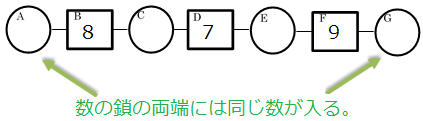

例題のように簡単に、単純な計算だけでは完成させられません。
ただし、時間が経過すればするほど、なんらかの方法で多くの生徒が鎖を完成させていました。
実際に生徒たちから出てきた解法を3種類紹介します。
Ⅲー② 数の鎖の主題の解法1(あてはめる)
1つ目の解法は、とにかくあてはめていく方法。
$~A=1~$のとき、
\begin{align*}
C&=B-A=8-1=7 \\
E&=D-C=7-7=0 \\
G&=F-E=9-0=9
\end{align*}であり、 $~A \neq G $なので不適。
$ A=2 $のとき、
\begin{align*}
C&=B-A=8-2=6 \\
E&=D-C=7-6=1 \\
G&=F-E=9-1=8
\end{align*}であり、 $~A \neq G $なので不適。
これを繰り返していくと、$ A=5 $のとき、
\begin{align*}
C&=B-A=8-5=3 \\
E&=D-C=7-3=4 \\
G&=F-E=9-4=5
\end{align*}となり、 $~A = G~ $なので、これで数の鎖が完成する。


多くの生徒が思いつける解法です。
中には、$~A~$が$~1~$増えると、$~G~$が$~1~$減ることに気付いた生徒もいました。
Ⅲー③ 数の鎖の主題の解法2(方程式を使う)
方程式の良さを実感できる解法がこちらです。
方程式の利用として使用する教材なので、この解法は是非生徒から引き出したいところ。
$~A=x~$とする。


すると、 $~C~,~E~,~G~$は次のように表せる。
\begin{align*}
C&=B-A=8-x \\
E&=D-C=7-(8-x)=-1+x \\
G&=F-E=9-(-1+x)=10-x
\end{align*}ここで、 $~A=G~$ なので、
\begin{align*}
x&=10-x \\
2x&=10 \\
x&=5 \\
\end{align*}と$~A=5~$が求まり、残りは代入することで数の鎖は完成する。
同じ方程式でも、次のような解法もありました。
$~A=G=x~$とする。


すると、 $~C~,~E~$は次のように表せる。
\begin{align*}
C&=B-A=8-x \\
E&=F-G=9-x \\
\end{align*}ここで、 $~C+E=D~$ なので、
\begin{align*}
(8-x)+(9-x)&=7 \\
17-2x&=7 \\
-2x&=-10 \\
x&=5
\end{align*}と$~A=G=5~$が求まり、残りは代入することで数の鎖は完成する。
同じ方程式による解法でも、こちらのほうが計算が簡単です。
$~x~$の置き方によって、計算の難易度が変わることにも気づかせたいですね。
Ⅲー④ 数の鎖の主題の解法3(等式の性質の利用)
方程式の利用という観点からは少しズレますが、方程式を解く上で欠かせない等式の性質をうまく利用した解法です。
$~A~,~B~,~C~$ の数の鎖から、
A+C=8~~~\cdots ①
$~C~,~D~,~E~$ の数の鎖から、
C+E=7~~~\cdots ②
$~E~,~F~,~G~$ の数の鎖から、
E+G=9~~~\cdots ③
となる。
$①$と$③$をたし算することで、
A+C+E+G=17
となり、ここに$②$を代入することで、
\begin{align*}
A+7+G&=17 \\
A+G&=10
\end{align*}が求まる。
ここで、$~A~$と$~G~$は同じ数なので、$~A=G=5~$と求まり、$①$と$③$にそれぞれ代入することで、$~C~,~E~$も求まるため、数の鎖は完成する。
小学生向けの賢い解法として紹介できる方法です。
実際、中学生もこの解法で解いている生徒は何人かいました。
Ⅲー⑤ 数の鎖の公式
以上の解法から、$~A~$と$~G~$に入る数を公式として思いつく生徒も出てきました。
それが、以下のような公式です。
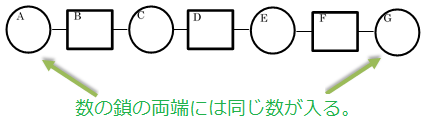

図10のような数の鎖において、次の式が成り立つ。
A=G=\frac{B+F-D}{2}先ほどの解法4をヒントに思いついた生徒もいれば、いくつか数の鎖の例を書いたときの数字の並びから気づいた生徒もいました。
主題を例にすれば、
A=G=\frac{8+9-7}{2}=5と確かに求まります。
この公式の証明も難しくはありません。
$~A~,~B~,~C~$ の数の鎖から、
A+C=B~~~\cdots ④
$~C~,~D~,~E~$ の数の鎖から、
C+E=D~~~\cdots ⑤
$~E~,~F~,~G~$ の数の鎖から、
E+G=F~~~\cdots ⑥
となる。
$④$と$⑥$をたし算することで、
A+C+E+G=B+F
となり、ここに$⑤$を代入することで、
\begin{align*}
A+D+G&=B+F \\
A+G&=B+F-D
\end{align*}が求まる。
ここで、$~G=A~$を代入すると、
\begin{align*}
A+A&=B+F-D \\
2A&=B+F-D \\
A&=\frac{B+F-D}{2}
\end{align*}と公式が求まった。 ■
この証明までたどり着けば、文字式の良さ、方程式の良さを感じさせながら、授業のまとめへと入れるでしょう。
Ⅳ 思考力をより高めるために(発展課題)
生徒たちが数の鎖に興味を持ってくれたら、さらに思考力を高める課題を出すこともできます。
それは、長さが9の数の鎖です。
Ⅳー① 数の鎖の発展課題
主題では、$~A~$から$~G~$の長さ7の数の鎖でした。
今度は$~A~$から$~I~$までの鎖となります。
次の数の鎖の両端には同じ数が入る。このとき、数の鎖を完成させなさい。
課題1


課題2


長さが7のときと違って、面白いことが起こります!
Ⅳー② 発展課題1の解答
あてはめ式で考えてあげると、課題1は$~A~$がどんな数でも完成することがわかります。






発展課題1のテーマは不定解でした。
「数学では答えが1つに定まる」という常識が、中1の段階で崩れることになります。
Ⅳー③ 発展課題2の解答
同じくあてはめ式で考えると、課題2は$~A~$がどんな数でも完成しないことがわかります。






以上のように、$~A~$が$~1~$増えたら$~I~$も$~1~$増えてしまうため、同じ数になることはありません。
発展課題2のテーマは不能解でした。
Ⅳー④ 長さ9の数の鎖の性質
実は、長さ9の数の鎖は不定解か不能解となります。
その見極め方が次のようなものになります。


<図19>のような長さ9の数の鎖では、次のような性質がある。
- $~ B+F=D+H~$のとき、$~A~$はどんな数でもあてはまる。(不定解)
- $~B+F\neq D+H~$のとき、$~A~$にあてはまる数は存在しない。(不能解)
こちらの性質に関する証明も、文字式で行えます。
$~A~,~B~,~C~$ の数の鎖から、
A+C=B~~~\cdots ⑦
$~C~,~D~,~E~$ の数の鎖から、
C+E=D~~~\cdots ⑧
$~E~,~F~,~G~$ の数の鎖から、
E+G=F~~~\cdots ⑨
$~G~,~H~,~I~$ の数の鎖から、
G+I=H~~~\cdots ⑩
となる。
$⑦+⑨-⑧-⑩~$より、
\begin{align*}
A+C+E+G-(C+E)-(G+I)&=B+F-D-H \\
A-I&=B+F-D-H \\
\end{align*}となる。
よって、$~B+F=D+H~$ならば、右辺は$~0~$となるため、$~A=H~$が成り立ち、
$~B+F \neq D+H~$ならば、右辺は$~0~$とならないため、$~A=H~$が成り立たない。 ■
このように、長さが7のときと同じように立式し、その式の意味を考えるという、思考力を育てる課題と言えるでしょう。



「数の鎖」、奥が深いね。



数学が好きな生徒は、自分でいろいろな鎖を作って探究するから、こちらが想像もしなかった性質を見つけてくることもあるよ。
「長さを増やしたら‥‥」とか「鎖のルールをかけ算にしたら‥‥」とかアレンジを加える生徒も多数いて面白かった!