
ジェロラモ・カルダノが発見者として名を残している三次方程式の解の公式。その内容と証明、さらには発見に至るまでの経緯について解説します。
- 三次方程式の解の公式ができるまでの歴史
- 解の公式の中身とその証明
- 解の公式の使い方
Ⅰ 歴史
まずは三次方程式がどういった流れで世の中に登場したのかを見てみましょう。
1545年、 ジェロラモ・カルダノ(Gerolamo Cardano , 1501-1576) が著書『アルス・マグナ』で3次方程式の解の公式について初めて述べました。しかしそれを元々発見したのは同じイタリア人の ニコロ・フォンタナ・タルタリア(Niccolò Fontana Tartaglia ,1500-1557) で、タルタリアは誰にも公表しないという約束で、カルダノに解き方を教えましたが、その約束を破ってカルダノは自分の本の中で公表してしまったのです。
タルタリアは自分の手柄を主張するべく、カルダノに数学試合(互いにいくつか問題を出し合い、期限までに解いた数が多いほうが勝ち)をしかけたものの、カルダノは弟子の ルドヴィコ・フェラーリ (Ludovico Ferrari , 1522-1565) を試合に出場させ、そのフェラーリが勝利。タルタリアは数学の表舞台から消え、3次方程式の解法の発見者はカルダノということで、名が世に通っています。


(出典:Unknown authorUnknown author, Public domain, via Wikimedia Commons)


(出典:See page for author, Public domain, via Wikimedia Commons)
タルタリアは、自分が見つけた公式をカルダノに横取りされた挙句、自分の数学力を見せつけるための数学試合でカルダノの弟子のフェラーリに負けるという屈辱を味わいました。
フェラーリは、カルダノと三次方程式の公式を本にまとめている中で、四次方程式の解の公式についても発見しています。
Ⅱ 解の公式と証明
Ⅱー① 解の公式
三次方程式
ax^3+bx^2+cx+d=0~~~~~~(a\neq0)
を変形してできる三次方程式
y^3+py+q=0
の解は、$~\omega=\displaystyle \frac{-1+\sqrt{3}i}{2}~$として、次の3つである。
\begin{align*}
y&=\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}} +\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}}\\
\\
y&=\omega~\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}} +\omega^2~\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}}\\
\\
y&=\omega^2~\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}} +\omega~\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}}\\
\\
\end{align*}この$~y~$を$~x~$にもどすことで、元の三次方程式の解も求められる。
$~x~$の三次方程式から$~y~$の三次方程式への変形方法は、Ⅱー② 証明を参照してください。
三次方程式なので、解は3つあり、以下のように1つの式にまとめて書き表すことも可能です。
y=\omega^k\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}} +\omega^{3-k}\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}} ~~~~~(k=~0~,~1~,~2)どのように三次方程式を変形すればいいのか、なぜ$~1~$の立方根が登場するのかを証明の中で見てみましょう。
Ⅱ-② 証明
多くの手順は踏みますが、その証明をステップに分けて解説していきます。
三次方程式
ax^3+bx^2+cx+d=0~~~~~(a\neq0)
の両辺を、$~a~$でわると、
x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}=0となる。
ここで、$~\displaystyle \frac{b}{a}=l~,~\frac{c}{a}=m~,~\frac{n}{a}=n~$とすれば、
x^3+lx^2+mx+n=0
となるため、$~\displaystyle y=x+\frac{l}{3}~$で置換して、左辺を計算すると、
\begin{align*}
&~~\left( y-\frac{l}{3} \right)^3+l\left( y-\frac{l}{3} \right)^2+m\left( y-\frac{l}{3} \right)+n \\
\\
&= \left( y^3-ly^2+\frac{l^2}{3}y-\frac{l^3}{27} \right)^3+l\left( y^2-\frac{2l}{3}y+\frac{l^2}{9} \right)^2+m\left( y-\frac{l}{3} \right)+n \\
\\
&=y^3-\left( b-\frac{l^2}{3} \right) y+\left(n-\frac{lm}{3}+\frac{2l^3}{27} \right)
\end{align*}である。
ここで、$~\displaystyle \left( b-\frac{l^2}{3} \right)=p~,~ \left(n-\frac{lm}{3}+\frac{2l^3}{27} \right) = q~$とすれば、すべての三次方程式が
y^3+py+q=0~~~~\cdots ①
の形で表すことができた。
$①$で、$~y=u+v~$と置き換えると、
(u+v)^3+p(u+v)+q=0
であり、これを展開して整理すると、
\begin{align*}
u^3+3u^2v+3uv^2+v^3+pu+pv+q&=0 \\
(u^3+v^3+q)+3uv(u+v)+p(u+v)&=0\\
(u^3+v^3+q)+(3uv+p)(u+v)&=0
\end{align*}となる。
したがって、連立方程式
\begin{cases}
&u^3+v^3+q=0 ~~~~\cdots ② \\
&3uv+p=0 ~~~~\cdots ③
\end{cases} を満たすような$~u~,~v~$が求まればよい。
$③$より、$~\displaystyle v=-\frac{p}{3u}~$なので、$②$に代入すると、
u^3-\left( \frac{p}{3} \right)^3\cdot \frac{1}{u^3}+q=0であり、両辺に$~u^3~$をかけることで、
u^6+qu^3-\left( \frac{p}{3} \right)^3=0 となる。
$~u^3=t~$とすると、
t^2+qt-\left( \frac{p}{3} \right)^3=0という$~t~$の二次方程式となる。
二次方程式の解の公式を使って、
\begin{align*}
t&=\frac{-q\pm \sqrt{q^2+4\left( \frac{p}{3} \right)^3 }}{2} \\
\\
&=-\frac{q}{2}\pm\sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 }
\end{align*}が求まる。
$~u~,~v~$の対称性と$②$から、$~\displaystyle \sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 }~$の符号を考えると、
\begin{cases}
\displaystyle u^3=-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 } ~~~\cdots ④\\
\\
\displaystyle v^3=-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 } ~~~\cdots ⑤\\ \end{cases}とわかる。
一般的に三次方程式$~x^3=A~$の解が、
x=\sqrt[3]{A} ~,~ \omega\sqrt[3]{A}~ ,~\omega^2\sqrt[3]{A} \\\left(\omega は1の立方根で、 \omega=-\frac{1}{2}+\frac{\sqrt{3}}{2}i \right) であることと、$③$より、$~uv~$が虚数とならないように、$~\omega~$の指数を考えると、$④$と$⑤$の解は以下の3パターンのみとなる。
\begin{cases}\displaystyle u=\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 }} \\
\\
\displaystyle v=\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 }} \\
\end{cases}\begin{cases}\displaystyle u=\omega~\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 }} \\
\\
v=\displaystyle \omega^2~\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 }} \\ \end{cases}\begin{cases}
\displaystyle u=\omega^2~\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 }} \\
\\
\displaystyle v=\omega~\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right) ^2 + \left( \frac{p}{3} \right) ^3 }} \\
\end{cases}以上より、3次方程式$~y^3+py+q=0 ~$の解の公式は、
\begin{align*}
y&=\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}} +\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}}\\
\\
y&=\omega~\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}} +\omega^2~\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}}\\
\\
y&=\omega^2~\sqrt[3]{-\frac{q}{2}+\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}} +\omega~\sqrt[3]{-\frac{q}{2}-\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3}}\\
\\
\end{align*}と表すことができる。■
$~u^3~,~v^3~$を対称性から定めて、それらから出てくる3種類の立方根を、積が虚数にならないように組み合わせてあげるのが難しいですね。
Ⅱ-③ 例
解の公式を使って、三次方程式を解いてみます。
次の三次方程式を解きなさい。
2x^3+6x^2-24x-36=0
普通だったら、両辺を$~2~$で割ったうえで、$~x=3~$という解を自力で見つけて、
\begin{align*}
x^3+3x^2-12x-18&=0 \\
(x-3)(x^2+6x+6)&=0 \\
x&=3~,~-3\pm\sqrt{3} ~~~\cdots ⑥
\end{align*}というように解きます。
では、これらの解を公式から導いてみましょう。
三次方程式
2x^3+6x^2-24x-36=0
の両辺を、$~2~$でわると、
x^3+3x^2-12x-18=0
となる。
$~\displaystyle y=x+1~$で置換して、左辺を計算すると、
\begin{align*}
&~~(y-1)^3+3(y-1)^2-12(y-1)-18 \\
&=y^3-3y^2+3y-1+3(y^2-2y+1)-12y+12-18 \\
&=y^3-3y^2+3y-1+3y^2-6y+3-12y+12-18 \\
&=y^3-15y-4 \\
\end{align*}である。
よって、
y^3-15y-4=0~~~~\cdots⑦
で、解の公式を使えばよい。
$⑦$から、$~p=-15~,~q=-4~$であるため、三次方程式の解の公式の3乗根の中身を先に計算すると、
\begin{align*}
&\displaystyle -\frac{q}{2}\pm\sqrt{\left( \frac{q}{2} \right)^2+\left( \frac{p}{3} \right)^3} \\
\\
&=-\frac{-4}{2}\pm\sqrt{\left( \frac{-4}{2} \right)^2+\left( \frac{-15}{3} \right)^3}\\
\\
&=2\pm\sqrt{4-125} \\
\\
&=2\pm11i \\
\\
&=(2\pm i)^3
\end{align*}となる。
よって、三次方程式の解の公式から、
\begin{align*}
y&=(2+i)+(2-i) \\
&=4 \\
\\
y&=\omega(2+i)+\omega^2(2-i) \\
\\
&=\left( -\frac{1}{2}+\frac{\sqrt{3}}{2}i \right)(2+i)+\left( -\frac{1}{2}-\frac{\sqrt{3}}{2}i \right)(2-i) \\
\\
&=-1-\frac{1}{2}i+\sqrt{3}i-\frac{\sqrt{3}}{2}-1+\frac{1}{2}i-\sqrt{3}i-\frac{\sqrt{3}}{2} \\
\\
&=-2-\sqrt{3} \\
\\
\\
y&=\omega^2(2+i)+\omega(2-i) \\
\\
&=\left( -\frac{1}{2}-\frac{\sqrt{3}}{2}i \right)(2+i)+\left( -\frac{1}{2}+\frac{\sqrt{3}}{2}i \right) (2-i) \\
\\
&=-1-\frac{1}{2}i-\sqrt{3}i+\frac{\sqrt{3}}{2}-1+\frac{1}{2}i+\sqrt{3}i+\frac{\sqrt{3}}{2} \\
\\
&=-2+\sqrt{3}
\end{align*}が求まる。
以上の3つの解$~y~$を、$~x=y-1~$にそれぞれ代入することで、
x=3~,~-3-\sqrt{3}~,~-3+\sqrt{3}~が求まった。
$⑥$と比較すれば、確かに解が求まっているとわかります。
$~y^3+py+q=0~$の形にすれば、あとは代入で解けるというのが解の公式らしさですね。
ただ、3乗根がうまく外れないと、ものすごく複雑な解になってしまいます。



カルダノ、ひどいヤツだなぁ。



解の公式の原型は、シピオーネ・デル・フェッロ(Scipione del Ferro , 1465-1526)という数学者が考えていたんだ。それをタルタリアが形にし、カルダノが公表したよ。
カルダノは、タルタリアではなく、フェッロからヒントを得たということにして、タルタリアとの約束を守ったことにしたんだ。



狡猾‥‥
参考文献
- 中村滋(2015)『数学史の小窓』 , pp.110-111 , 日本評論社
- テオニ・パパス著 , 熊原啓作訳(2019)『数学スキャンダル』 , p145-151 , 日本評論社
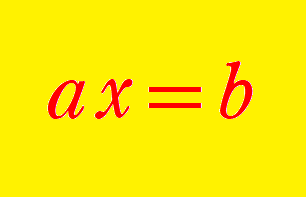
コメント
コメント一覧 (2件)
この公式を使わないと厳しい問題ってあるんですか??
森北出版株式会社が出している『数学検定1級 実践演習』(財団法人 日本数学検定協会監修、中村力 著)のp47に以下のような問題がありました。
\( \sqrt[3]{6+\sqrt{\frac{980}{27}}}+\sqrt[3]{6-\sqrt{\frac{980}{27}}} \)について次の問いに答えなさい.
①この数はある3次の代数方程式の解の1つです.この方程式を求めなさい.
②(略)
この問題では、3次方程式の解の公式を使うと、簡単に解けます。