永遠に到達できない？ゼノンの二分法のパラドックスを徹底解説！

　2m先のゴールには、いくら進んでもたどり着けない

　こんな直感に反する状況を、さも当たり前のように示したのが「二分法のパラドックス」です。

　この記事では、

• 「二分法のパラドックス」って何？
• 誰が何のために発案したの？
• パラドックスはどうすれば解決できるの？

という疑問を解消するために、パラドックスの内容とその解決方法、そしてそのパラドックスが提示された歴史的文脈について、数学教員がわかりやすく解説しています。

　この記事を読むことで、二分法のパラドックスを深く理解することができます。

二分法のパラドックスとは？

　「二分」というのは「半分に分けること」。

　二分法のパラドックスとは、距離を半分に分けていったときに生じるパラドックス（矛盾）のことです。

目的地に永遠にたどり着けない矛盾

　二分法のパラドックスは、ゼノンが提示した一連のパラドックスの中でも特に知られています。

 二分法のパラドックス

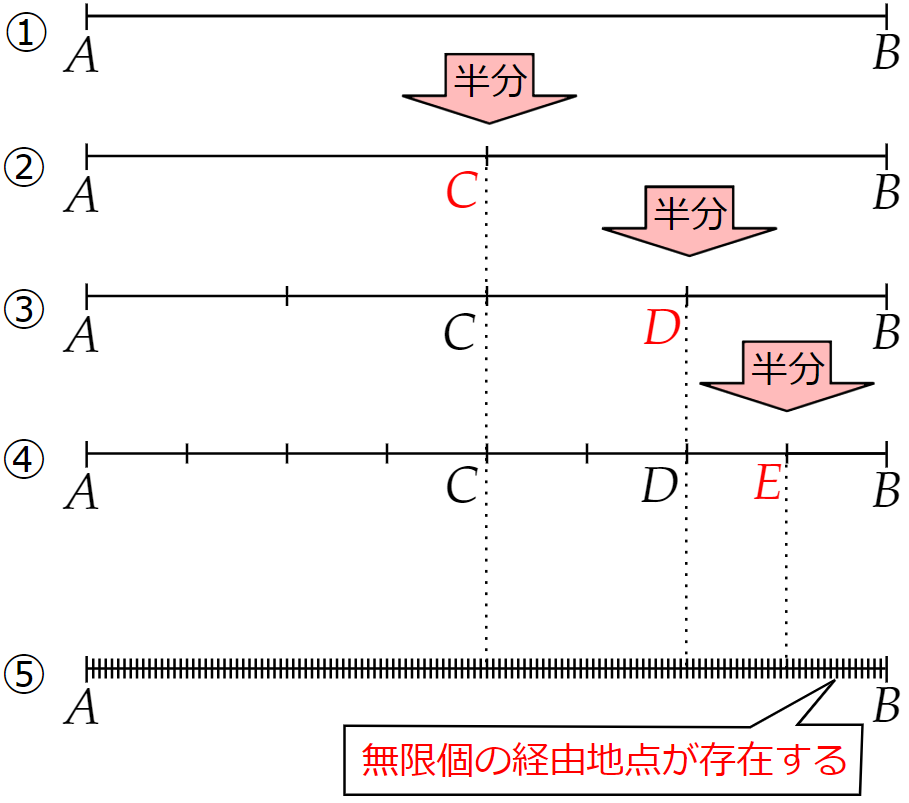
• 　$~A~$から$~B~$まで移動するとき、
• 　$~A~$と$~B~$の中間点である$~C~$を経由する必要がある。
• 　$~C~$から$~B~$まで移動するとき、中間点である$~D~$を経由する必要がある。
• 　$~D~$から$~B~$まで移動するとき、中間点である$~E~$を経由する必要がある。
• 　これを無限に繰り返していくと、無限個の経由地点が必要であり、有限の時間内に到達するのは不可能である。

　より具体的に考えてみましょう。

 二分法のパラドックスの例

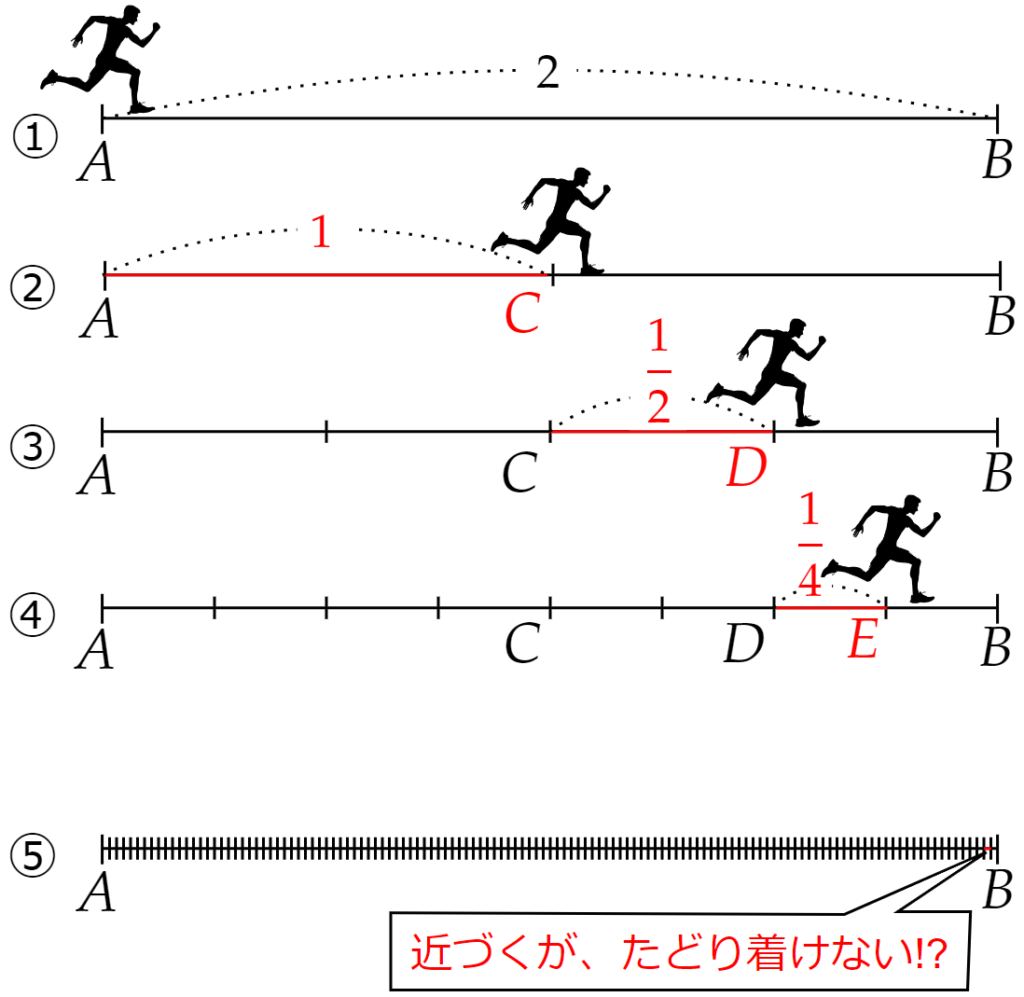
　$~AB=2~$m の距離を移動することを考える。

• 　$~A~$から$~2~$m先にある$~B~$まで移動するとき、
• 　$~1~$m進み、$~C~$に到達する。
• 　$~0.5~$m進み、$~D~$に到達する。
• 　$~0.25~$m進み、$~E~$に到達する。
• 　常に残りの距離の半分を進むことになるため、$~B~$に到達することはできない。

　この説明によれば、たった$~2~$mの距離を走り切ることが不可能になります。

　現実では当然あり得ないことなので、その感覚のズレが「パラドックス（矛盾）」という名につながっています。

哲学者ゼノンが提起したパラドックスの１つ

　二分法のパラドックスは、古代ギリシャの哲学者ゼノン（Zeno , B.C.490頃-B.C.430頃）によって提起されました。

　当時のギリシャ数学を引っ張っていたデモクリトスなどのミレトス派の考え方に対し、エレア派のゼノンは二分法のパラドックスをはじめとする４つのパラドックスを提示することで、ミレトス派を論破したのです。

デモクリトス

空間の根源は点、時間の根源は瞬間！
これで運動の連続性を説明できる。

ゼノン

でも、無限個の点で距離を分割すると、$~2~$mの距離すら走り切れないことが説明できちゃうよ。

デモクリトス

うぅ‥‥。

　ゼノンが提示したパラドックスにより、その後の数学者たちは無限や無限小を考える際に慎重な思考が求められました。

あわせて読みたい

哲学者ゼノンのパラドックスはなぜ生まれた？ゼノンが後世に与えた影響とは？【数学史6－7】 古代ギリシャの哲学者ゼノンの生涯と彼が提案したパラドックスを解説しています。タレスやピタゴラスなどのミレトス学派を批判するために提示されたゼノンのパラドックスは、後の数学において無限を扱う際の大きな障壁となりました。この記事により、ゼノンのパラドックスの内容だけでなく、数学史に与えた影響を知ることができます。

二分法のパラドックスはどう解決されるのか？

　紀元前のギリシャでは、二分法のパラドックスに対する反論はできませんでした。

　しかし、現代数学における無限の考え方を使うと簡単に解決されます。

残りの距離の極限による解決

　 二分法のパラドックスの例で考えたとき、$~n~$回目の経由地に達した後の残りの距離は、$~\displaystyle \frac{1}{2^{n-1}}~$mと表すことができます。

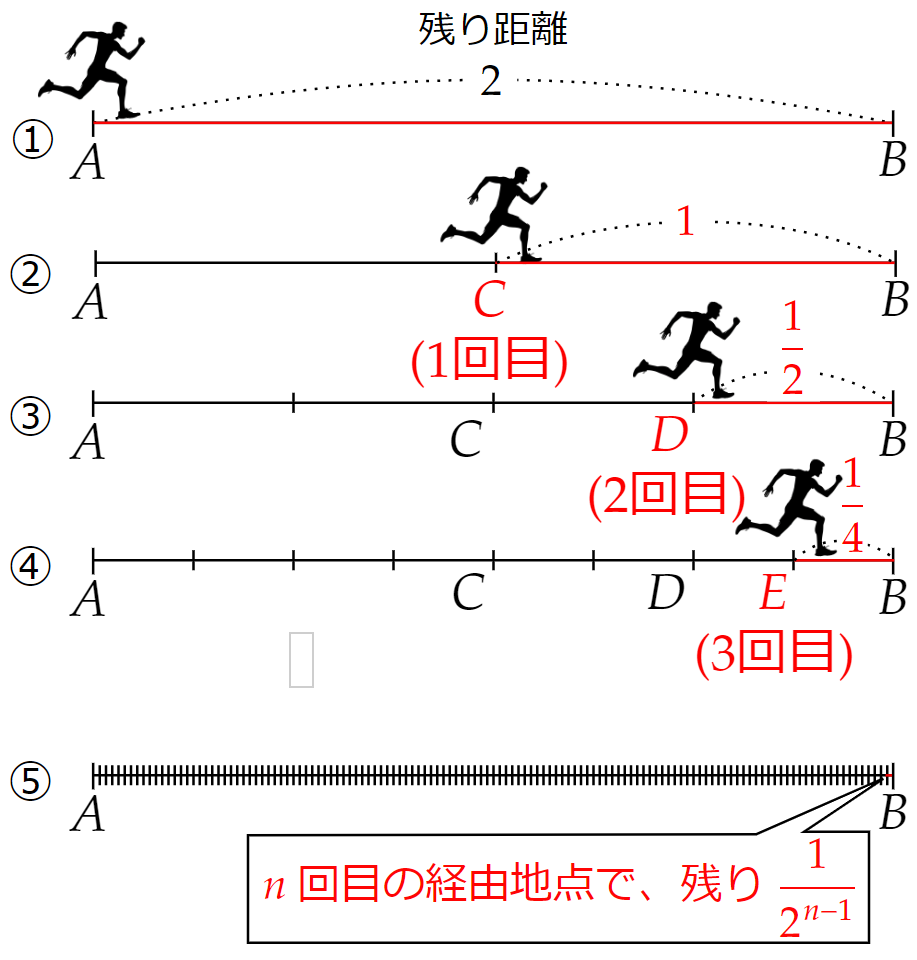
　この$~n~$を限りなく大きくし、無限大に近づけると、

\lim_{n\to \infty}\frac{1}{2^{n-1}}=0

となるため、残りの距離は$~0~$になることがわかります。

無限等比級数による解決

　残りの距離ではなく、進んだ距離の合計を求めることでも、二分法のパラドックスは解決に導けます。

　 二分法のパラドックスの例において、各段階で進む距離は

1~,~\frac{1}{2}~,~\frac{1}{4}~,~\frac{1}{8}~,~\cdots

という等比数列をなし、この数列の和、すなわち無限等比級数の和は公比$~r~$が$~-1 \leqq r \leqq 1~$を満たすため収束します。

　具体的には、初項$~1~$、公比$~\displaystyle \frac{1}{2}~$なので

\begin{align*}
1+\frac{1}{2}+\frac{1}{4}+\cdots &=\frac{1}{1-\frac{1}{2}}  \\
\\
&=\frac{1}{\frac{1}{2}}  \\
\\
&=2
\end{align*}

となり、ゴールにたどり着いていることがわかります。

　無限に数をたしても、その和が無限になるとは限らないという点が、このパラドックスの解決の鍵です。

面積でパラドックスをとらえる

　進んだ距離の合計

1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots

という無限に続く計算を、長方形の面積で表すと次のような図となります。

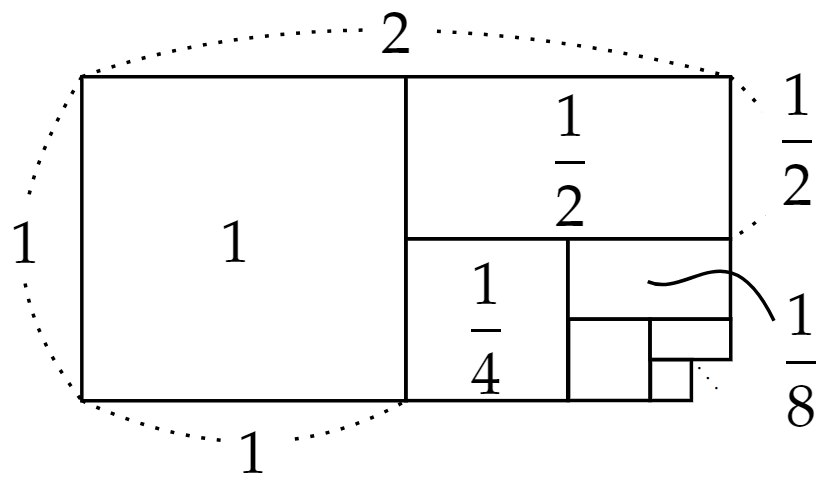
　面積$~1~$の正方形に始まり、その半分の長方形をたし、さらにその半分の長方形をたし‥‥と無限に繰り返した場合、全体の面積が無限に大きくなることはなく、その和は$~2~$に収束します。

　無限の小さな部分が合わさっても、有限の全体を形成するということが直感的にわかるでしょう。

まとめ：無限に数を足しても、無限大になるとは限らない

　二分法のパラドックスは、無限という概念が直感に反することを示す古典的な例です。

• 運動の連続性を主張するミレトス派に対し、エレア派のゼノンが提示したパラドックスの１種。
• 無限に数をたしても、無限大になるとは限らないところがパラドックスのミソ。
• 無限等比級数の収束性により、パラドックスが解決された。

数学を知らないと、永遠に到達できないことを納得させられちゃいそう。　

ゼノンのパラドックスを解決する術が無かったため、これ以降の数学者たちは無限を恐れてしまったんだ。