三平方の定理の証明⑬～外接円と直角二等辺三角形を利用した証明をわかりやすく解説！～

　図１のように、$~a < b~$である直角三角形$~ABC~$の外接円 $~O~$を描く。

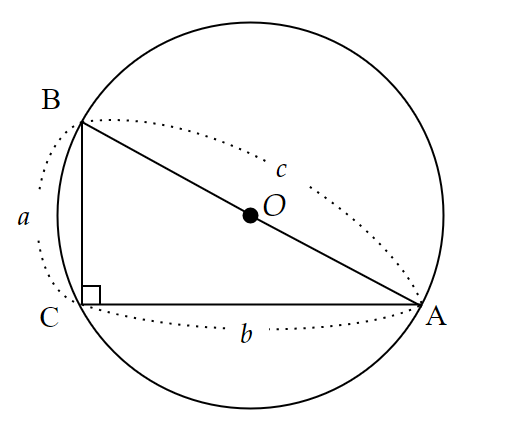
　次に、直線$~AC~$上に、$~CD=a~$となるような$~D~$を図２のようにとる。

　このとき、$~\triangle BCD~$は直角二等辺三角形となる。

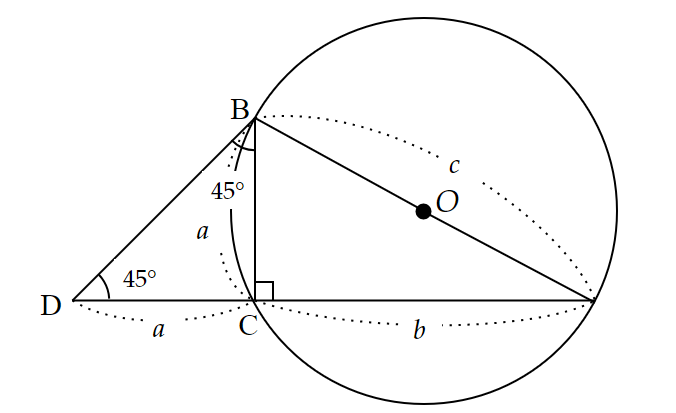
　さらに、図３のように、直線$~DB~$と円$~O~$の$~B~$ではない交点を$~E~$とし、さらに直線$~AE~$と直線$~BC~$の交点を$~F~$とする。

　このとき、$~\angle BEF=90^{\circ}~$であり、対頂角から$~\angle BEF=45^{\circ}~$なので、$~\triangle BEF~$も直角二等辺三角形となる。

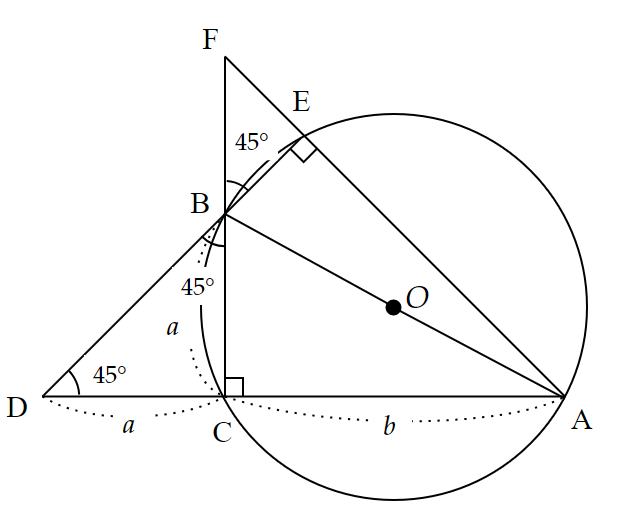
　また、$~\angle BCA=90^{\circ}~$であることから、$~\triangle ACF~$も直角二等辺三角形である。

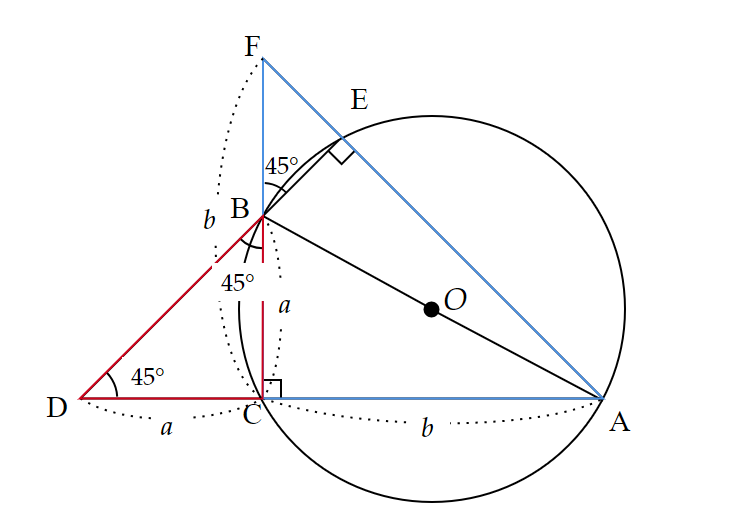
　四角形$~AFBD~$の面積$~S~$は、図４から

\begin{align*}
S&=\triangle BCD+\triangle ACF \\
&=\frac{a^2}{2}+\frac{b^2}{2}~~~~\cdots ①
\end{align*}

と表せる。

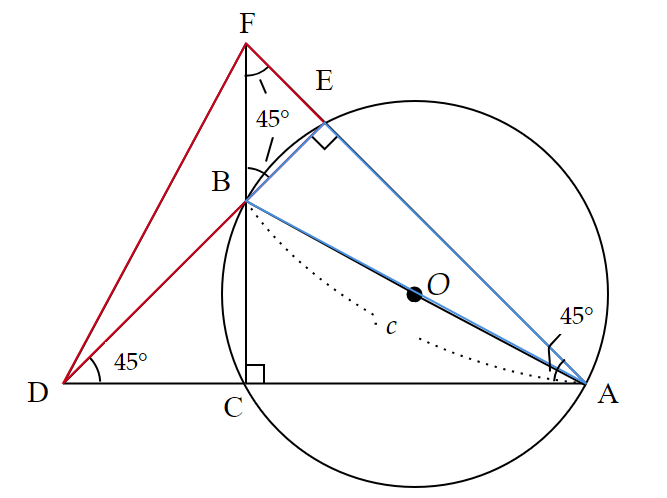
　ところで、$~\triangle EFD~$と$~\triangle EBA~$において、

\begin{align*}
EF&=EB ~~~~\cdots ②\\
\angle FED&=\angle BEA=90^{\circ} ~~~~\cdots ③\\
\end{align*}

であり、$~\triangle AED~$も直角二等辺三角形であることから、

ED=EA~~~~\cdots ④

となるため、$②$～$④$より二辺夾角相等で$~\triangle EFD \equiv \triangle EBA~$とわかる。

　よって、

FD=BA=c

が求まる。

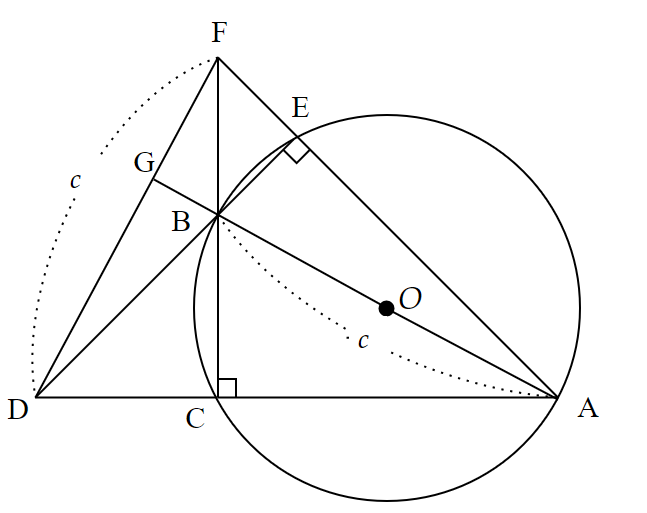
　さらに、$~DE \perp AF~,~FC \perp AD~$であることから、$~DE~$と$~FC~$の交点$~B~$は、$~\triangle ADF~$の垂心である。

　したがって、直線$~AB~$と$~FD~$の交点を $~G~$とすると、$~AG \perp FD~$である。

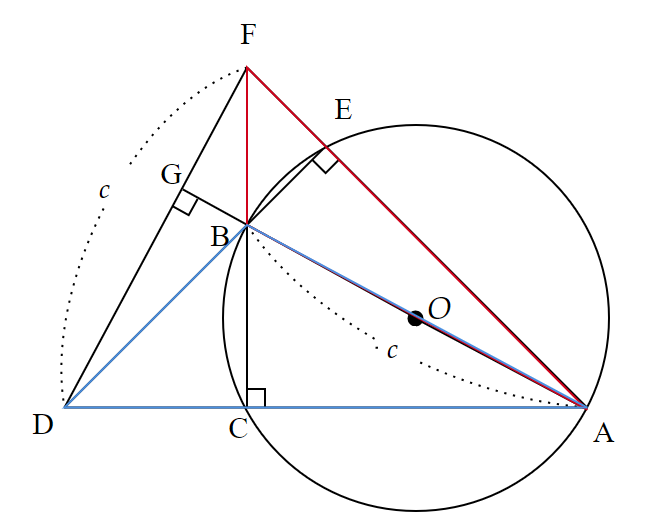
　以上より、四角形$~AFBD~$の面積$~S~$は、

\begin{align*}
S&=\triangle FBA+\triangle DBA \\
\\
&=c \cdot FG \cdot \frac{1}{2}+c \cdot DG \cdot \frac{1}{2} \\
\\
&=\frac{c}{2}(FG+DG) \\
\\
&=\frac{c}{2}\cdot c \\
\\
&=\frac{c^2}{2} ~~~\cdots ⑤
\end{align*}

と表せる。

　$①~,~⑤~$より、

\begin{align*}
\frac{a^2}{2}+\frac{b^2}{2}&=\frac{c^2}{2} \\
\\
a^2+b^2&=c^2
\end{align*}

が示された。■