三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。
19~20世紀においても、アメリカの大統領であるガーフィールドや、アメリカの16歳の女子高校生コンディットが、それ以前には無かった証明方法を見つけています。
この記事では、ガーフィールドとコンディットのそれぞれの証明方法について、現役数学教員がわかりやすく解説します。
ガーフィールドは単純な方法、コンディットは複雑な方法と対照的ではありますが、近代アメリカの数学者ではない2人の証明方法を味わってみましょう。
- アメリカの大統領ジェームズ・A・ガーフィールドについて
- ガーフィールドの三平方の定理の証明方法
- アメリカの女子高校生アン・コンディットについて
- コンディットの三平方の定理の証明方法
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓

ジェームズ・A・ガーフィールドについて
ジェームズ・A・ガーフィールド(James Abram Garfield , 1831-1881)は、アメリカ合衆国の政治家・弁護士です。

(出典:Unknown; part of Brady-Handy Photograph Collection., Public domain, via Wikimedia Commons)
1863年に共和党員として下院議員に選出され、1881年3月から第20代米国大統領になりました。
しかし、1881年7月に銃撃を受け、同年9月に死去。在任期間はわずか半年でした。
ガーフィールドは最も博学の大統領であり、片手でラテン語、もう一方の手でギリシャ語を同時に書くことができたと言われています。
議員時代の1876年、ガーフィールドは他の国会議員たちと数学の議論をしているときに、三平方の定理の証明をふと思いつきました。
ガーフィールドの証明
政治家であるガーフィールドが思いついた証明方法は、台形を使ったシンプルなものです。
直角三角形$~ABC~$において、半直線$~CA~$上に$~AD=a~$となる$~D~$をとる。
次に、$~AD~$に垂直な線分$~DE~$を$~B~$と同じ側に作り、$~AE~$を結ぶ。
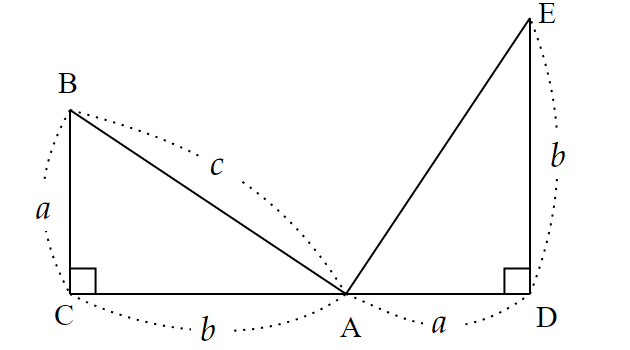
このとき、$~\triangle ABC~$と$~\triangle EAD~$において、
\begin{align*}
& AC=ED=b \\
& BC=AD=a \\
& \angle ACB=\angle EDA=90^{\circ}
\end{align*}であるため、二辺夾角相等から$~\triangle ABC \equiv \triangle EAD~$。
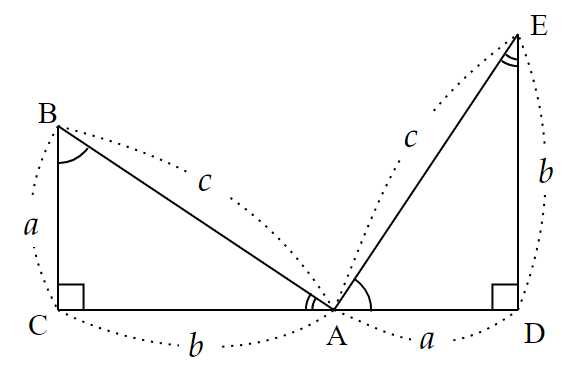
したがって、
\begin{align*}&EA=AB=c \\
&\angle EAD=\angle ABC ~~~\cdots ①
\end{align*}である。
次に、$~\angle BAE~$を求める。
位置関係から、
\angle BAE=180^{\circ}-(\angle BAC+\angle EAD)となり、$①$を代入すると、
\begin{align*}
\angle BAE&=180^{\circ}-(\angle BAC+\angle ABC) \\
&=180^{\circ}-90^{\circ} \\
&=90^{\circ}
\end{align*}と求まる。
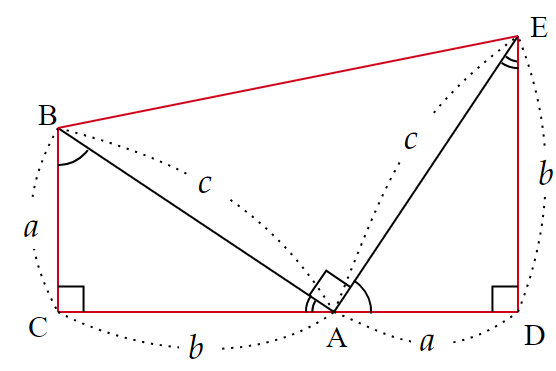
ここで、台形$~BCDE~$の面積$~S~$は
\begin{align*}
S&=(a+b)\times (a+b) \times \frac{1}{2} \\
\\
&=\frac{(a+b)^2}{2} ~~~~\cdots ②
\end{align*}と表せる。
また、$~S~$は$~\triangle ABC~,~\triangle ABC~,~\triangle ABC~$の3つの直角三角形の和から
\begin{align*}
S&=a \times b \times \frac{1}{2}+a \times b \times \frac{1}{2}+c \times c \times \frac{1}{2} \\
\\
&=\frac{ab}{2}+\frac{ab}{2}+\frac{c^2}{2} \\
\\
&=ab+\frac{c^2}{2} ~~~~\cdots ③
\end{align*}とも表せる。
$②$と$③$より、
\begin{align*}
\frac{(a+b)^2}{2}&=ab+\frac{c^2}{2} \\
\\
(a+b)^2&=2ab+c^2 \\
\\
a^2+2ab+b^2&=2ab+c^2 \\
\\
a^2+b^2&=c^2
\end{align*}から、三平方の定理は示された。■
台形の面積を2通りで表すという、よくある発想に基づいた証明方法でした。
ただ、数学者でもない45歳政治家の考案という事実が、この証明を有名にしています。
アン・コンディットについて
同じアメリカ国内で、20世紀に三平方の定理の別証を思いついた女子高校生がいました。
彼女の名前はアン・コンディット(Ann Cindit , 1922-不明)で、インディアナ州サウスベンド中央中等・高等学校に在学中の16歳の時に、証明を公開しました。

『ピタゴラスの命題』という、三平方の定理の証明を集めた本を書いた イライシャ・スコット・ルーミス(Elisha Scott Loomis , 1582-1940) は、コンディットのことを以下のように評しています。

“ この16歳の少女は,インド , ギリシア , 現代の大数学者が誰一人としてこれまでにやったことのなかったことをやった.使われたすべての補助線 , すべての三角形が斜辺の中点から始まるように工夫された証明は初めてである.アン・コンディットの証明という名を付けなければいけない”
E・マオール『ピタゴラスの定理』より引用。ルーミスの写真は Finkel, B. F., Public domain, via Wikimedia Commonsより改変。
ルーミスの言葉からもわかるように、コンディットの証明は補助線をうまく使った証明法となります。
アン・コンディットの証明
「大数学者が誰一人としてこれまでやったことのなかった」ともあるように、補助線が非常に複雑な証明方法になります。
ゆっくり読み進めてください。
$~c~$を斜辺とする直角三角形$~ABC~$において、$~AB~,~BC~,~CA~$をそれぞれ1辺とした正方形 $~AEDB~,~BCFG~,~CAHI~$を外側に作り、$~FI~$を結ぶ。
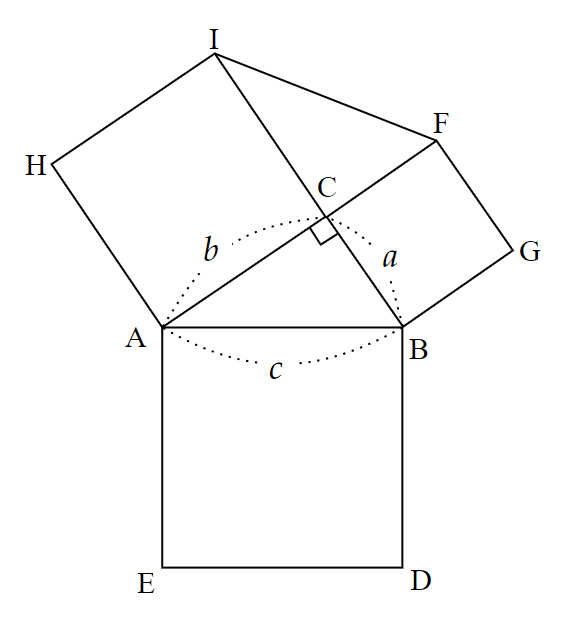

$~AB~$の中点を$~P~$とし、直線$~CP~$と$~FI~$の交点を$~R~$とする。
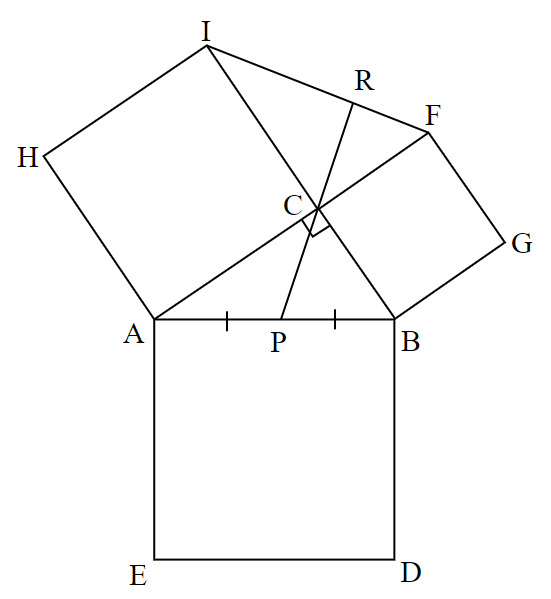

このとき、$~\angle ACB=90^{\circ}~$であるため、$~AB~$を直径とした$~\triangle ABC~$の外接円の中心が $~P~$ となる。
そのため、半径であることから
AP=PC ~~~\cdots ④
が成り立つ。
また、$~\triangle ABC~$と$~\triangle IFC~$において、
AC=IC \\
BC=FC \\
\angle ACB=\angle ICF=90^{\circ} であるため、二辺夾角相等より$~\triangle ABC \equiv \triangle IFC~$。
よって、
\begin{align*}
AB=IF &\cdots ⑤ \\
\angle BAC=\angle FIC &\cdots ⑥
\end{align*}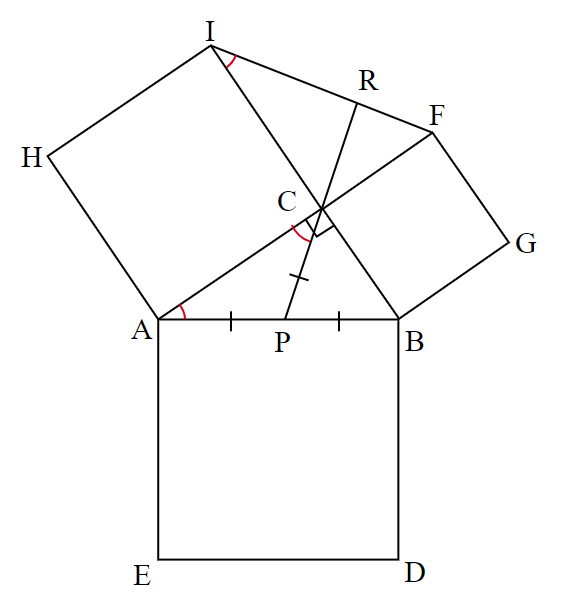

$④$より、 $~\triangle APC~$ は二等辺三角形なので、
\angle BAC=\angle PCA \cdots ⑦
であり、$⑥$と$⑦$より、
\angle FIC=\angle PCA \cdots ⑧
とわかる。
また、$~\triangle CIR~$で外角の性質から
\angle FIC+\angle IRC=\angle PCA +90^{\circ}であり、$⑧$を使うと、
\angle IRC=90^{\circ} \cdots ⑨とわかる。
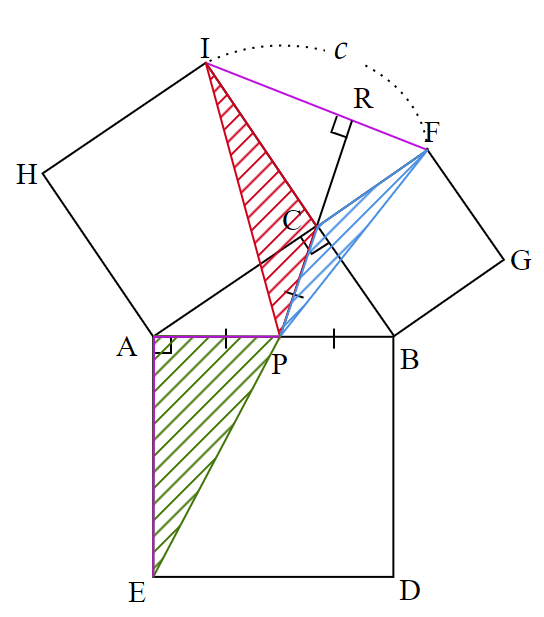

次に、$~\triangle PIC~$と$~\triangle PFC~$に注目する。
それぞれ$~PC~$を底辺としたとき、$⑨$より、$~PR \perp IF~$なので、
\begin{align*}
\triangle PIC&=\frac{1}{2}\times PC \times IR \\
\\
\triangle PFC&=\frac{1}{2}\times PC \times RF \\
\end{align*}であるため、
\begin{align*}
\triangle PIC+\triangle PFC&=\frac{1}{2}\times PC \times (IR+RF) \\
\\
&= \frac{1}{2}\times PC \times IF
\end{align*}となり、$⑤$より
\begin{align*}
\triangle PIC+\triangle PFC&=\frac{1}{2}\times PC \times AB ~~\cdots ⑩
\end{align*}である。
また、$~\triangle AEP~$にも注目すると、
\triangle AEP=\frac{1}{2}\times AP \times AE であり、$④$や正方形の性質から、
\triangle AEP=\frac{1}{2}\times PC \times AB ~~~\cdots ⑪とわかる。
$⑩$と$⑪$より、
\triangle PIC+\triangle PFC=\triangle AEP~~~\cdots⑫
が成り立つ。
次に、$~ED~,~FG~,~HI~$の中点を$~L~,~M~,~N~$として、それらを$~P~$と結ぶと、正方形の各辺とそれぞれ平行になる。
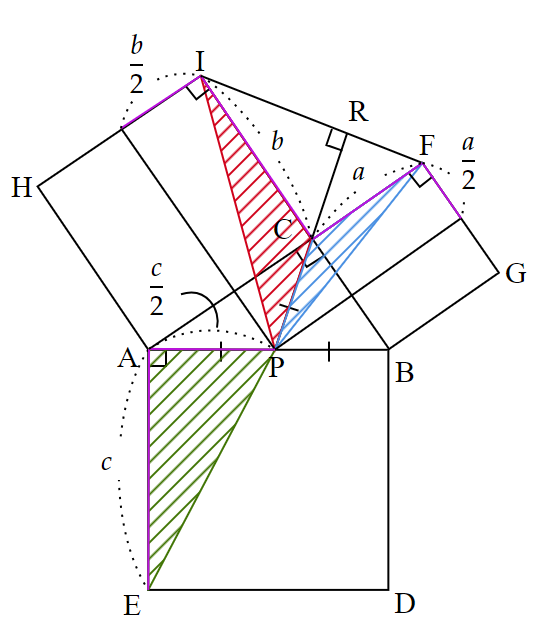

$~\triangle PIC~$の面積は、$~IC~$を底辺とすると、
\begin{align*}
\triangle PIC&= \frac{1}{2} \times IC \times NI \\
\\
&=\frac{1}{2}\times AC \times \left( \frac{1}{2}AC \right) \\
\\
&=\frac{1}{4}b^2 ~~~\cdots ⑬
\end{align*}である。
同様に、$~\triangle PFC~$の面積は、$~FC~$を底辺とすると、
\begin{align*}
\triangle PFC&=\frac{1}{2} \times FC \times MF \\
\\
&=\frac{1}{2}\times BC \times \left( \frac{1}{2}BC \right) \\
\\
&=\frac{1}{4}a^2 ~~~\cdots ⑭
\end{align*}となり、$~\triangle AEP~$の面積は、
\begin{align*}
\triangle AEP&=\frac{1}{2} \times AP \times AE \\
\\
&=\frac{1}{2}\times AB \times \left( \frac{1}{2}AB \right) \\
\\
&=\frac{1}{4}c^2 ~~~\cdots ⑮
\end{align*}と求まる。
最後に、$⑬$~$⑮~$を$⑫$に代入することで、
\begin{align*}
\frac{1}{4}a^2+\frac{1}{4}b^2&=\frac{1}{4}c^2\\
\\
a^2+b^2&=c^2
\end{align*}となり、三平方の定理は示された。■
奇抜な補助線によって、三角形の面積を2通りで表してつなげるという証明方法でした。



ガーフィールドの「他の国会議員たちと数学の議論」という状況がシュール。



そこで「ふと思いつく」っていうのがすごいよね。
しかも、その流れで自分の証明を認めてもらおうと学会に提出する行動力もすごい。
コンディットの行動力と発想にも感服。
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓



コメント