2022年も残りわずか。
2023年が近づくにつれて、
$2023$は素数なのか?
$2023$ってどんな数なんだろう?
と気になっている方向けに、$~2023~$という数について現役数学教員が解説!
毎年、西暦を使った数学ネタを年賀状にしているため、今回もいろいろと研究してみました。
実は、$~2023~$は$~7~$で割れる数であるだけでなく、幸運数やハーシャッド数、ピタゴラス数などにも登場するんです!
2023を素因数分解してわかること
まずは、2023を素因数分解してみましょう。
2023=7 \times 17^2
$~2~,~3~,~5~$で割れないため、何で割れるか一見わかりづらいです。
2023は7の倍数である
素因数分解の結果からもわかるように、$~2023~$は$~7~$で割れます。
実際に割ってみればわかりますが、以下のような7の倍数判定法を使うこともできます。
一の位から3桁ごとに区切り、それらを交互に加減した結果が7の倍数であれば、 その自然数は7の倍数である 。
この判定法によれば、$~2023~$を$~2~$と$~023~$に分けて交互にたし算・ひき算すると、
-2+23=21
となり、$~21~$が$~7~$の倍数であるため、$~2023~$は$~7~$の倍数とわかります。

$~7~$で割れることがわかれば、$~2023 \div 7=289~$より、$~289=17^2~$により素因数分解が完了します。
17の倍数判定法も一応存在しますが、$~17^2~$は覚えておくと何かと便利です。
2023の約数は6個で総和は2456
$~2023=7 \times 17^2~$という素因数分解の結果から、以下のような計算をすることで、$~2023~$の約数の個数が$~6~$個、約数の総和が$~2456~$とわかります。
$~2023=7^1 \times 17^2~$より、約数の個数は
(1+1)\times (2+1)=6~(個)
とわかる。
また、約数の総和については
\begin{align*}
(1+7) \times (1+17+17^2)&=8 \times 307 \\
&=2456
\end{align*}とわかる。
計算式だけだと難しく思えますが、以下のような表で整理するとわかりやすいです。
| 約数 | $~1~$ | $~17~$ | $~17^2~$ |
| $~1~$ | $~1~$ | $~17~$ | $~289~$ |
| $~7~$ | $~7~$ | $~119~$ | $~2023~$ |
$~2023~$の約数は$~1~,~7~,~17~,~119~,~289~,~2023~$であり、自身($2023$)を除く約数の和は$~433~$となるため、$~2023~$は不足数(自身以外の約数の和が、自身よりも小さくなる数)と言うこともできます。
2023が最大となるピタゴラス数は2組
$~a^2+b^2=c^2~$を満たす自然数$~a~,~b~,~c~$の組(ピタゴラス数)でも、2023が出てきます。
$~a~$や$~b~$に入る際の組み合わせは列挙しきれないものの、$~c~$に2023が入るのは、
(a,b,c)=(952,1785,2023)~,~(1127,1680,2023)
の2組しかありません。
Excelを使えば簡単に見つけられる
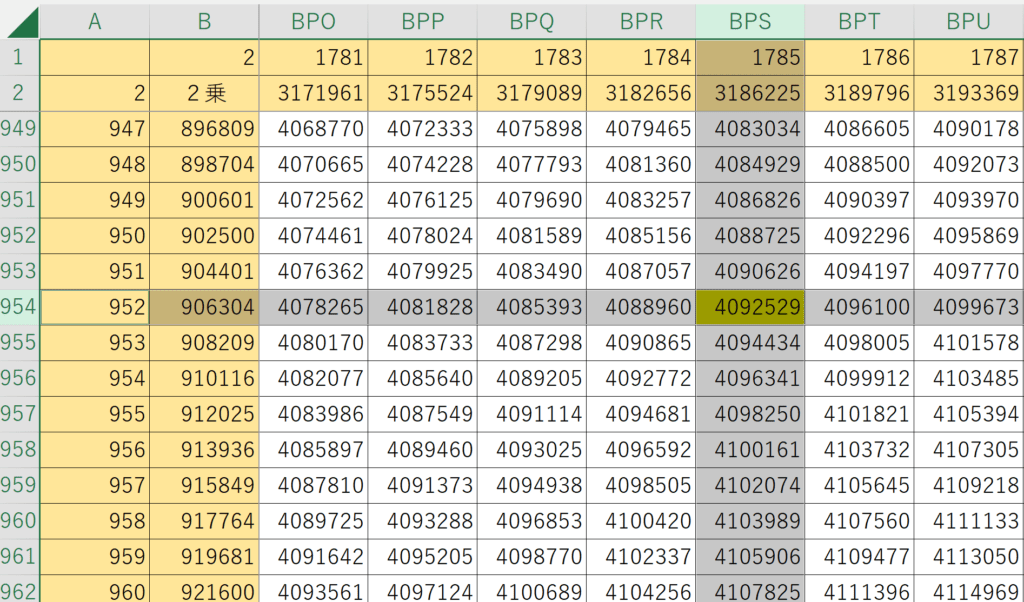
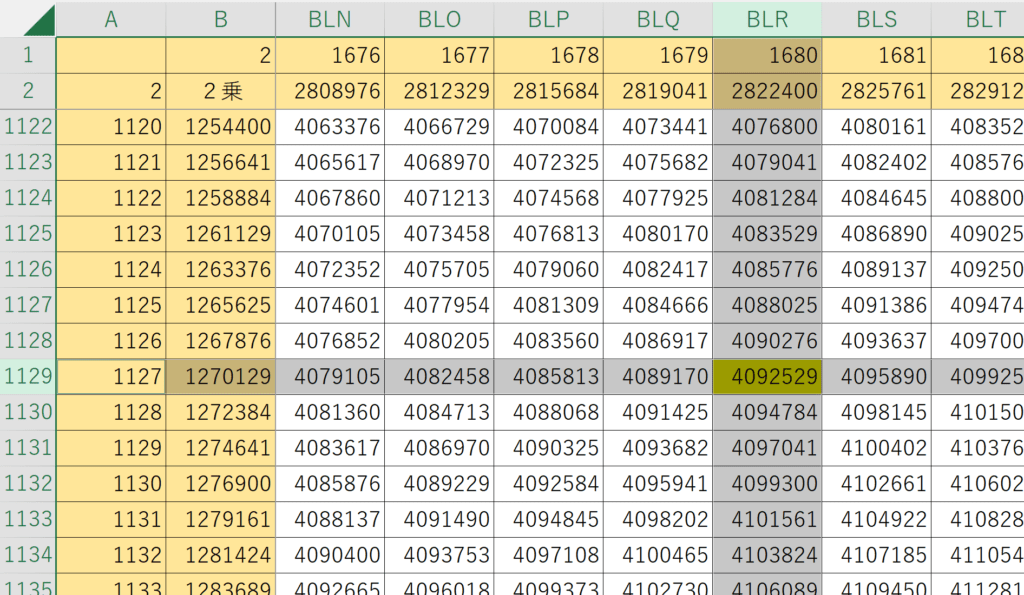
Excelで平方数の加法表を作成し、検索ツールで$~4092529=(2023^2)~$を探すことで、$~2023~$が最大となるピタゴラス数の組は見つけられます。
実際の計算画面は図2、図3のようなものになります。
1組は手計算でも求められる
1組目の$~a=952~,~b=1785~,~c=2023~$は、機械に頼らなくても簡単に求まります。
なぜなら、$~8~,~15~,~17~$の直角三角形を$~119$~倍に拡大するだけだからです。
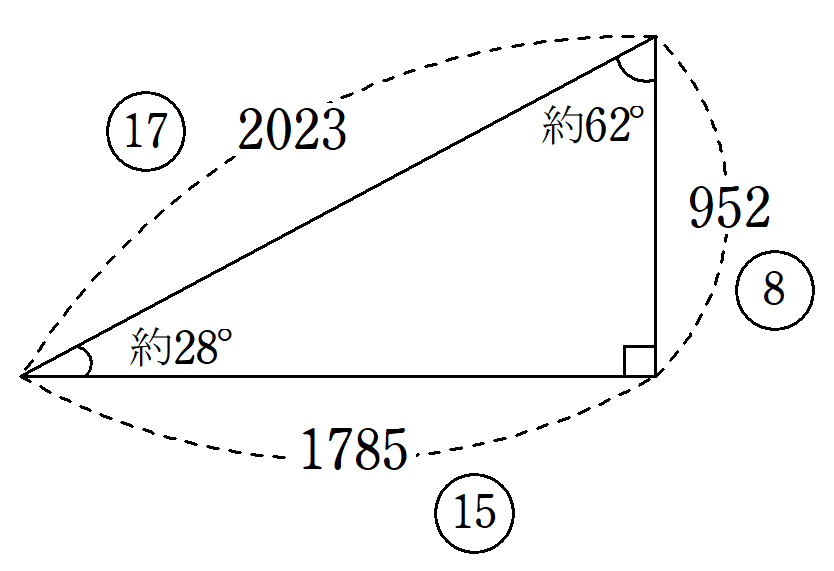
ここでも、$~2023=7 \times 17^2=119 \times 17~$という素因数分解の結果が利用できました。
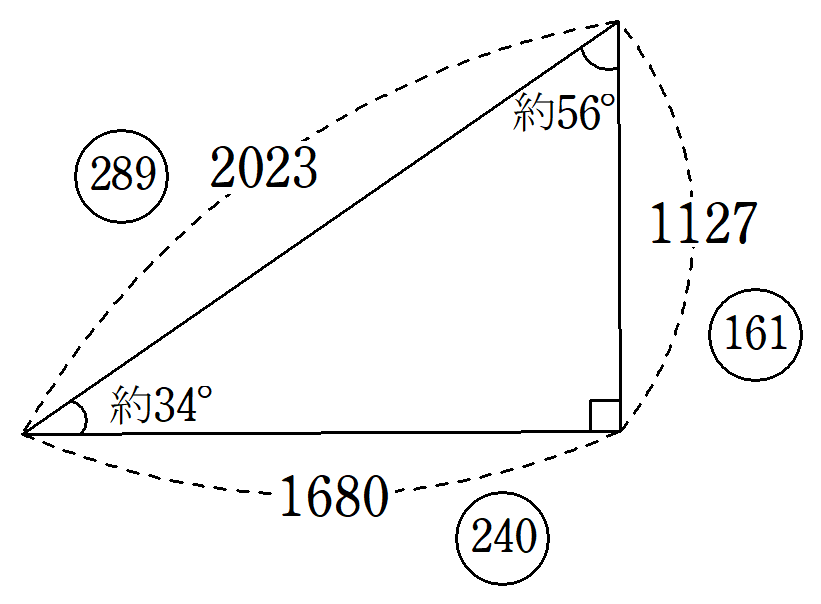
また、$~a=1127~,~b=1680~,~c=2023~$の組については、最大公約数が$~7~$であるため、$~161~,~240~,~289~$を三辺に持つ直角三角形を$~7~$倍に拡大したものとなります。
2023が登場する数列
オンライン整数列大辞典(OEIS)を利用し、2023が登場する数列を調べてみました。
検索結果の中から、有名な数列や、シンプルでおもしろい数列を抜粋して紹介します。
279番目の幸運数
$~2023~$は$~279~$番目の幸運数(lucky number)です。
幸運数とは、以下のような作り方で生まれる自然数の列となります。
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,\cdots
1,3,5,7,9,11,13,15,17,19,21,\cdots
この時点で、$~3~$が幸運数であると決まる。($~1~$も幸運数)
1,~,3,7,9,13,15,19,21,\cdots
この時点で、$~7~$が幸運数であると決まる。
1,3,7,9,13,15,21,\cdots
この時点で、$~9~$が幸運数であると決まる。
1,3,7,9,13,15,21,25,31,33,37,43,49,51,63,67,69,73,75,79,87,93,99,\cdots
こうして完成した幸運数の列の279番目が2023となります。
408番目のハーシャッド数
$~2023~$は408番目のハーシャッド数(harshad number)です。
ハーシャッド数の定義は次のように与えられます。
自然数の各位の和が、もとの自然数の約数に含まれている数をハーシャッド数という。
$~2021~$と$~2023~$を例にハーシャッド数かどうかを判別してみましょう。
$~2021~$の各位の和は$~2+0+2+2=5~$。
$~2021~$の約数は、$~1~,~43~,~47~,~2021~$であり、各位の和である$~5~$が含まれていないため、$~2021~$はハーシャッド数ではない。
$~2023~$の各位の和は$~2+0+2+3=7~$。
$~2023~$の約数は、$~1~,~7~,~17~,~119~,~289~,~2023~$であり、各位の和である$~7~$が含まれているため、$~2023~$はハーシャッド数である。
ちなみに、$~2022~,~2023~,~2024~,~2025~$は連続したハーシャッド数になります。(そんなに珍しくはない性質ですが‥‥)
7の7乗を7の階乗で割った余りが2023
最後にシンプルな数式に登場する$~2023~$を1つ。
7^7 \div 7!= 163 \cdots 2023
$~7^7=823543$を$~7!=5040~$で割ると、余りが$~2023~$となる美しい数式です。
$~n^n~$を$~n!~$で割ったときの余りに関する数列の7番目の項となります。
0, 0, 3, 16, 5, 576, 2023, 4096, 227529,\cdots
まとめ
$~2023~$に関して、素因数分解をはじめ、マニアックな数列まで取り上げてきました。
- $~2023=7 \times 17^2~$と素因数分解できる。
- 2種類の直角三角形の斜辺に$~2023~$が登場する。
- 幸運数やハーシャッド数、$~n^2~$を$~n!~$で割った余りなどの数列に$~2023~$が登場する。
最後の$~7^7 \div 7!= 163 \cdots 2023~$に関しては、次のように言い換えることができます。
7^7 \equiv 2023 ~~~\pmod {~7!~}$~2023~$が$~7~$に囲まれた縁起の良い数式です。
2023年、よい年になりますように。

コメント
コメント一覧 (4件)
素数界隈でじわじわと話題になっているものです。
2023年に刊行された本が面白かった、というよりは、かつてない衝撃でした。URLはプレスリリースサイトですので安心して開いて頂けますが、一応、リリースタイトルと一緒に貼っておきます。
「素数の出現法則」、ついに発見される! 既成概念を根底からくつがえす現象、果たして証明できるのか!?
https://prtimes.jp/main/html/rd/p/000000002.000107904.html
のりさん
コメントありがとうございます。
プレスリリースを拝見いたしましたが、面白そうな内容ですね!
小難しい感じではなく、小説調というところが読みやすそうです。
読みたい本リストに加えさせていただきました。
今抱えている仕事が終わったら、読んでみたいと思います。
素敵な情報ありがとうございました。
ハーシャッド数かどうかの判別例
~2022~ 2022 の各位の和は~2+0+2+2=6~ 2+0+2+2=6 。
~2022~ 2022 の約数は、~1~,~2~,~3~,~6~,~337~,~674~,~1011~,~2022~ 1 , 2 , 3 , 6 , 337 , 674 , 1011 , 2022 であり、各位の和である~6~ 6 が含まれていないため、~2022~ 2022 はハーシャッド数ではない。
のところ、6が含まれているような気がするんですけどどういうことでしょうか?
あやみさん
コメントありがとうございます。
まさにその通りで、大変な勘違いをしておりました。
ハーシャッド数ではない例を2021に変更いたします。
ご指摘いただき、非常に助かりました。
今後ともよろしくお願いします。