
Ⅰ コーシーの収束判定法と例
19世紀、オーギュスタン・ルイ・コーシー(Augustin Louis Cauchy)が発見した、級数が収束するかどうかを判定するための方法を、「コーシーの収束判定法」と言います。
まずは、判定法の内容を見てみましょう。
正項級数(すべての$~n~$に対し、$~a_n \ge 0~$となる級数)$~\displaystyle \sum_{n=1}^{\infty}a_n~$において、
\begin{equation}
\ell=\lim_{n \to \infty}\sqrt[n]{a_n}
\end{equation}
としたとき、この級数の収束性は次のように判断できる。
\begin{cases}
0 \le \ell < 1 &のとき、\displaystyle \sum_{n=1}^{\infty}a_n~は収束する。 \\
1 < \ell &のとき、\displaystyle \sum_{n=1}^{\infty}a_n~は発散する。 \\
\end{cases}
「ダランベールの収束判定法」と同様、$~\ell=1~$のときは、収束することもあれば発散することもあるため、判定できません。
$~\ell=1~$の場合も含め、実際に例を挙げていきます。
$~\displaystyle \sum_{n=1}^{\infty} \left( \frac{n+1}{2n+3} \right)^n~$の収束性を判定する。
$~a_n=\displaystyle \left( \frac{n+1}{2n+3} \right)^n~$として、コーシーの収束判定法を使うと、
\begin{align}
\ell&=\lim_{n \to \infty} \sqrt[n]{\left( \frac{n+1}{2n+3} \right)^n} \\
\\
&=\lim_{n \to \infty}\frac{n+1}{2n+3} \\
\\
&=\lim_{n \to \infty}\frac{1+\frac{1}{n}}{2+\frac{3}{n}} \\
\\
&=\frac{1}{2}~~( < 1 )
\end{align}
となるため、$~\displaystyle \sum_{n=1}^{\infty}\left( \frac{n+1}{2n+3} \right)^n~$は収束する。
ちなみに、Excelでこの級数を計算し、$~\displaystyle \sum_{k=1}^{n} a_k~$を縦軸、$~n~$を横軸とすると、
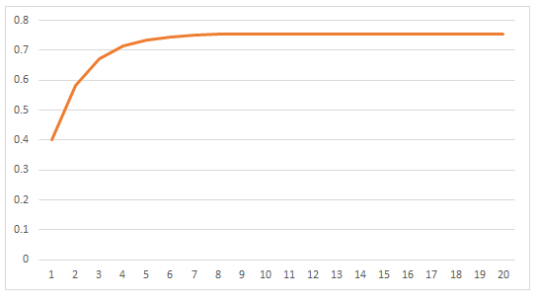
となり、$~n=20~$の時点で$~0.755576~$となりました。
$~\displaystyle \sum_{n=1}^{\infty}\left( 1+\frac{1}{n} \right)^{n^2}~$の収束性を判定する。
$~a_n=\displaystyle \left( 1+\frac{1}{n} \right)^{n^2}~$として、コーシーの収束判定法を使うと、
\begin{align}
\ell&=\lim_{n \to \infty}\sqrt[n]{\left( 1+\frac{1}{n} \right)^{n^2}} \\
\\
&=\lim_{n \to \infty}\left( 1+\frac{1}{n} \right)^{n^2 \cdot \frac{1}{n}} \\
\\
&=\lim_{n \to \infty}\left( 1+\frac{1}{n} \right)^n \\
\\
&=e~~( > 1 )
\end{align}
となるため、$~\displaystyle \sum_{n=1}^{\infty}\left( 1+\frac{1}{n} \right)^{n^2}~$は発散する。
Excelで発散の様子をグラフにしてみました。
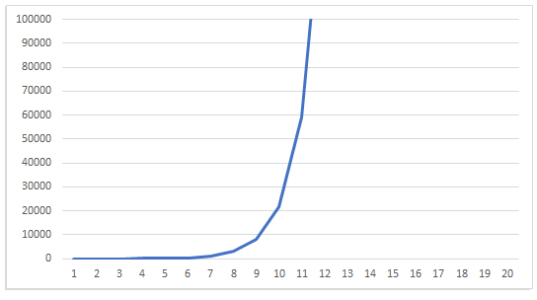
$~n=10~$あたりから爆発的に大きくなっています。
$~\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^{\log{n}}}~$の収束性を判定する。
$~a_n=\displaystyle \frac{1}{n^{\log{n}}}~$として、コーシーの収束判定法を使うと、
\begin{align}
\ell&=\lim_{n \to \infty}\sqrt[n]{\frac{1}{n^{\log{n}}}} \\
\\
&=\lim_{n \to \infty}\sqrt[n]{n^{-\log{n}}} \\
\\
&=\lim_{n \to \infty}n^{-\frac{\log{n}}{n}} \\
\end{align}
となる。
ここで、指数に注目すると、発散の速さから
\begin{equation}
\lim_{n \to \infty}\frac{\log{n}}{n}=0
\end{equation}
であるため、
\begin{equation}
\ell=1
\end{equation}
となり、$~\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^{\log{n}}}~$が収束するかどうかは判定できない。
この級数は、十分大きな$~n~$で、$~\log{n} > 2~$であることを利用すると、
\begin{align}
n^{\log{n}} &< n^2 \\
\frac{1}{n^{\log{n}}} &> \frac{1}{n^2} \\
\end{align}
となるため、「ダランベールの収束判定法」より$~\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}~$が収束することから、$~\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^{\log{n}}}~$も収束します。
実際、グラフにしてみると約$~2.238~$に収束します。
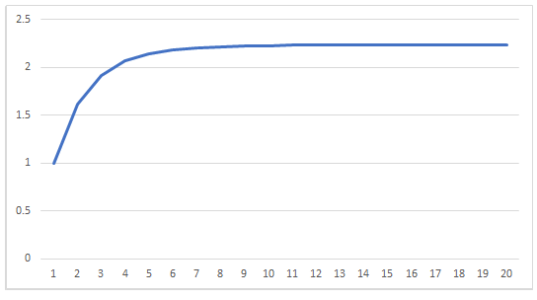
$~\displaystyle \sum_{n=1}^{\infty}\frac{(n+1)^n}{n^{n+1}}~$の収束性を判定する。
$~a_n=\displaystyle \frac{(n+1)^n}{n^{n+1}}~$として、コーシーの収束判定法を使うと、
\begin{align}
\ell&=\lim_{n \to \infty} \sqrt[n]{\frac{(n+1)^n}{n^{n+1}}} \\
\\
&=\lim_{n \to \infty} \sqrt[n]{\frac{(n+1)^n}{n^n \cdot n}} \\
\\
&=\lim_{n \to \infty} \frac{n+1}{n}\cdot \frac{1}{n^{\frac{1}{n}}} \\
\\
&=\lim_{n \to \infty} \frac{1+\frac{1}{n}}{1}\cdot \frac{1}{n^{\frac{1}{n}}} \\
\\
&=1\cdot 1 \\
\\
&=1
\end{align}
となるため、$~\displaystyle \sum_{n=1}^{\infty}\frac{(n+1)^n}{n^{n+1}}~$が収束するかどうかは判定できない。
この級数については、
\begin{align}
a_n-\frac{1}{n}&=\frac{(n+1)^n}{n^{n+1}}-\frac{1}{n} \\
\\
&=\frac{(n+1)^n-n^n}{n^{n+1}}
\end{align}
を考えることで、$~(n+1)^n-n^n > 0~$であるため、
\begin{align}
a_n-\frac{1}{n} &> 0 \\
\\
a_n &> \frac{1}{n}
\end{align}
とわかります。
「ダランベールの収束判定法」によって、$~\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}~$が発散することから、$~\displaystyle \sum_{n=1}^{\infty}a_n~$も発散することがわかります。
実際の発散の様子は以下の通りです。
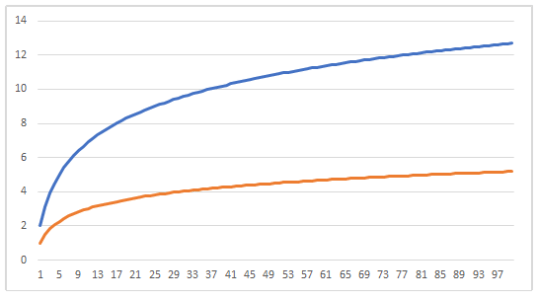
非常に緩やかですが発散します。
$~\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}~$と比べることで、自分を納得させましょう。(笑)
例3、例4からもわかる通り、$~\ell=1~$のときは、収束することもあれば、発散することもあり、判定を行うことができません。
Ⅱ 証明
コーシーの収束判定法の証明は、「ダランベールの収束判定法」の証明と同じ流れで行えます。
\begin{equation}
\ell=\lim_{n \to \infty}\sqrt[n]{a_n} < 1
\end{equation}
を言い換えると、ある自然数$~N~$が存在して、$~n \ge N~$となるすべての自然数$~n~$について、
\begin{equation}
0 < \sqrt[n]{a_n} < 1
\end{equation}
が成り立つということである。
ここで、$~0 < \sqrt[n]{a_n} < k < 1~$となるような$~k~$をとれば、
\begin{equation}
0 < a_n < k^n < 1
\end{equation}
であり、$~\displaystyle \sum_{n=N}^{\infty} k^n~$は収束するため、$~\displaystyle \sum_{n=N}^{\infty}a_n~$も収束する。
よって、
\begin{equation}
\sum_{n=1}^{\infty}a_n=\underbrace{\sum_{n=1}^{N-1}a_n}_{定数}+\sum_{n=N}^{\infty}a_n
\end{equation}
は収束する。$~~~\blacksquare~$
また、$~\displaystyle \ell=\lim_{n \to \infty}\sqrt[n]{a_n} > 1~$も同様に考え、
\begin{equation}
a_n > 1
\end{equation}
となり、$~\displaystyle \sum_{n=N}^{\infty} 1~$は発散するため、$~\displaystyle \sum_{n=N}^{\infty}a_n~$も発散する。
よって、$~\displaystyle \sum_{n=1}^{\infty}a_n~$も発散する。$~~~\blacksquare~$


◇参考文献等
・杉浦光夫・清水英男・金子晃・岡本和夫(2014)『基礎数学7 解析演習』,pp.51-55,東京大学出版会.
・「数学ノート」,<https://math-note.com/dalembert-ratio-test/> 2020年11月8日アクセス
コメント