生徒が苦手意識を持ちやすい教科である数学。
そういった生徒たちの関心意欲を高めるために、生徒が主体的に取り組める数学的活動を授業の中で入れることが望ましいものの、
- 数学的活動は授業準備に時間がかかる(教員が忙しすぎる)
- カリキュラムの進行上、授業時数的に数学的活動をする余裕がない
といった理由から、例題→問題演習→例題→問題演習→‥‥となってしまいがちです。
しかし、そういった縛りの中でも、授業内に小ネタを挟むことで生徒の興味を惹いたり、数学が楽しいと思えるような授業を手軽に展開することができます。
この記事では、1回の授業の中で「1へぇー&1笑い」を実践し続けている現役数学教員が、中1の単元「正負の数」で使っている数学ネタを紹介!
準備不要で5分後の授業からでも使えます!!
この記事は随時更新していきます。
-(マイナス)記号の由来は?
この単元で登場する$~-~$(マイナス)記号。
ひき算でもおなじみですが、この記号の由来はどこにあるのでしょうか?
“minus”の頭文字”m”をくずして書いた
ドイツの数学者ヨハネス・ウィッドマン(Johannes Widman , 1460頃-16世紀初め)が、1489年に記した『算術』で初めて$~-~$が数学記号として用いられました。

(出典:Unknown sourceUnknown source, Public domain, via Wikimedia Commons)
ウィッドマンの『算術』以前は、ひき算の記号として$~\tilde{m}~$が使われていましたが、ウィッドマンが$~\tilde{m}~$の$~m~$をくずして書くことで、横棒1本へと変化していきました。

+ や × , ÷ , = の由来も知っておこう
この話をすると当然登場するのが、

$~+~$や$~\times~$はどのように生まれたんですかー?
という質問です。
下の表にざっくりとまとめておきます。
| 記号 | 関係する人物 | 由来 |
| $~+~$ | ヨハネス・ウィッドマン(1492) | “and”を意味するラテン語”et”をくずして書いた。 |
| $~-~$ | ヨハネス・ウィッドマン(1492) | “minus”の頭文字”m”をくずして書いた。 |
| $~\times~$ | ウィリアム・オートレッド(1631) | 分数計算の書式でクロスした斜め線が使われた。 |
| $~\div~$ | ヨハン・ハインリヒ・ラーン(1659) | 分数の形$~\displaystyle \frac{○}{○}~$からできた。 |
| $~=~$ | ロバート・レコード(1557) | 等しいものの象徴として、平行線が元々使われていて、それが短くなってできた。 |
以上の記号の由来を合わせて知っておくと、入学して間もない生徒に「中学校の先生すげー」と思わせられるでしょう。
なぜ「正負」の数と言うのか?
一般的に、「正」の反対は「誤」。「負」の反対は「勝」。
なぜ「正」と「負」の数なのでしょうか?
起源は中国の数学書『九章算術』
そもそも$~0~$よりも小さい数の概念は、紀元前2世紀頃の中国で使われた計算器具「算木」で初めて登場しました。
赤の算木が正の数、黒の算木が負の数を意味し、算木の並べ方に従って正負の整数を表しています。
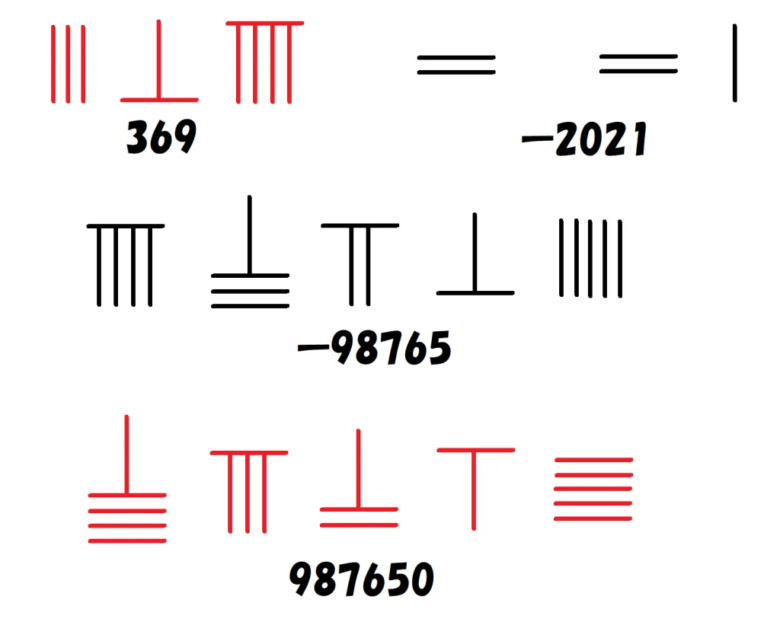

「正負」いう言葉が登場するのも中国が最初であり、紀元前の中国の数学書『九章算術』8章第3問に以下のような表現が載っています。
正負術に関して、ひき算については同符号の$~2~$数は互いに引き、異符号の$~2~$数は互いに加える。
$~0~$から正を引けばこれを負とし、$~0~$から負を引けばこれを正とする。
たし算については異符号の$~2~$数は互いに引き、同符号の$~2~$数は互いに加える。
$~0~$に正を加えればこれを正とし、$~0~$に負を加えればこれを負とする。
2000年以上も前から、正負の数のたし算・ひき算の方法が知られていた証拠となっています。
征服することが「正」しく、「負」けるときは敗走
『九章算術』において、$~0~$より大きい数を「正」、$~0~$より小さい数を「負」とした理由について、確かなことはわかっていません。
ただ、『九章算術』が成立するよりも前、紀元前8世紀頃から紀元前221年までの中国は春秋・戦国時代であり、度重なる戦の経験と数の表し方が以下のように結びついたという説があります。
戦の中で、自軍が相手を攻めることは正義であり、その正義に従って戦います。
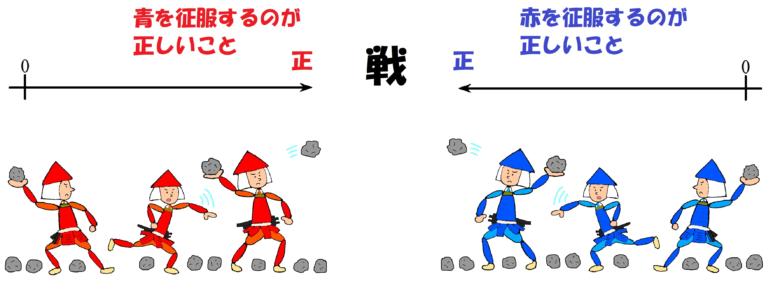

青軍が優勢になれば、赤軍は攻めるときと逆方向に敗走することになります。
すなわち、戦の負けを意味します。
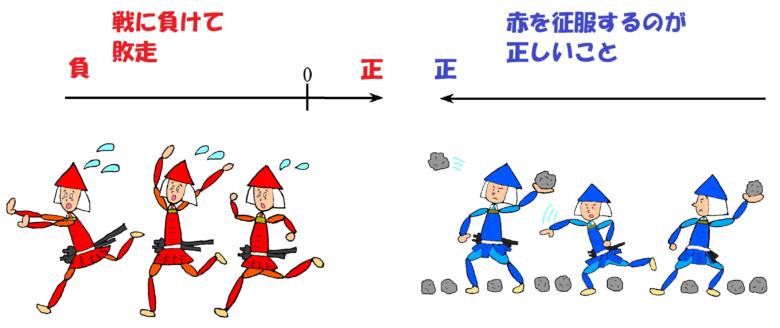

確かにこの説であれば、正の反対が負であり、数直線のイメージとも合致しています。
交換法則や結合法則が成り立たない例
加法や乗法で登場する交換法則と結合法則。
減法や除法で成り立たないことは有名ですが、中学生がわかるレベルで成り立たない例はあるのでしょうか?
指数計算では成り立たない
まず、同じ単元で出てくる指数の計算においては、交換法則も結合法則も成り立ちません。
\begin{align*}
2^3&=8 \\
3^2&=9
\end{align*}より、もとの数(底)と指数の交換法則は成り立たない。
\begin{align*}
(2^2)^3&=4^3=64 \\
2^{(2^3)}&=2^8=256
\end{align*}より、結合法則は成り立たない。
結合法則の例に関しては、中学数学の範囲を出てしまう内容なので、
「($2$の$2$乗)の$3$乗」と「$2$の($2$の$3$乗)乗」
と黒板に書くことで、謎解きのように楽しめます。
身近な例でも成り立たない
身近な例で考えると、交換法則や結合法則はもっと成り立ちません。
中学生になったばかりということで、制服を例に考えてみましょう。
まずは交換法則について、以下のように成り立ちません。


また、結合法則も同じように考えられます。
(Yシャツ+ネクタイ)+ブレザー → Yシャツを着て、ネクタイをしたあと、ブレザーを着る。
Yシャツ+(ネクタイ+ブレザー) → ネクタイをし、ブレザーを着たあと、Yシャツを着る??
逆に、(カルピス原液+水)=(水+カルピス原液)のように成り立つ例もあるため、このように生活と結びつけると笑いがとれるでしょう。
サイコロの転がし方でも交換法則は成り立たない
意外性があるのは、サイコロの転がし方です。
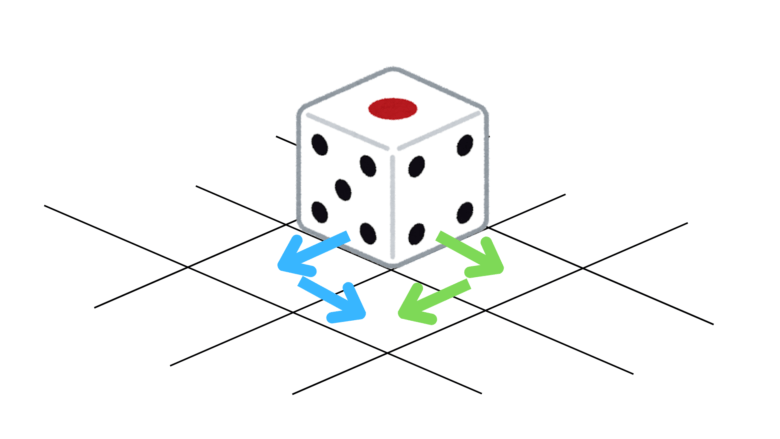

上の図のようなサイコロを、マス目に沿って転がすことを考える。
左下→右下 、右下→左下 という2通りの転がし方をしたとき、サイコロの上面の目はそれぞれいくつになっているか求めなさい。
到着するマスは同じですが、転がし方によって上面の目が違ってきます。(左下→右下なら3、右下→左下なら2)
もっとシンプルなものだと、「2歩進んで右を向く」と「右を向いてから2歩進む」も交換法則の成り立たない例として挙げることができます。
納豆で使われている分配法則
計算を便利に行う分配法則ですが、生活上でも分配法則の表記が役立っているんです。
納豆の食品表示は数式で表されている
納豆の食品表示では、大体どのメーカーでも次のような表し方をしています。


きちんとした数式にすると、以下のようになります。
(納豆40g+たれ6g+からし0.7g)\times2=納豆80g+たれ12g+からし1.4g
左辺の表記にすることで、1パックあたりの納豆とたれとからしの量だけでなく、それが何パック入っているかを一目で読み取ることができますね。
マイナス × マイナス はなぜ プラス になる?
この単元の最も有名な質問は、「負の数×負の数がなぜ正の数になるのか?」 というもの。
中1向けの解答方法を2つ紹介します。
教科書に1つは載っているため、もう1つの方法を知識として持っていると小ネタとして活躍させられるでしょう。
かける数を1つずつ減らしていく
まず、$~(負の数)\times(正の数)~$は、かけ算のもともとの考え方より、
\begin{align*}
(-2)\times 3&=(-2)+(-2)+(-2) \\
&=-6
\end{align*}と計算できます。($~-2~$が$~3~$個)
これを利用し、次のような数列パズルを考えます。
\begin{align*}
(-2)\times 3&=-6 \\
(-2)\times 2&=-4 \\
(-2)\times 1&=-2 \\
(-2)\times 0&=0 \\
(-2)\times (-1)&=\Box \\
(-2)\times (-2)&=\Box \\
(-2)\times (-3)&=\Box \\
\end{align*}
$~-2~$にかける数を$~1~$減らすと、積は$~2~$増えています。
この考え方から、すべての$~\Box~$が埋まり、$~(負の数)\times(負の数)=(正の数)~$であることがわかります。
速さと距離を利用する
この単元の始めに出てくる、「西に$~5~$km移動する」を「東に$~-5~$km移動する」と表現できることを利用します。
主題となるのはこんな問題。
問題自体は簡単ですが、問題の後半を式にすると、次のようになります。
(−2)×(−3)=6
負の数の表し方の復習も兼ねて、話題に出すのもアリな方法でした。
わり算で逆数をかける理由
小学校の算数で頻出の質問が、分数を割るときに分数をひっくり返してかける理由。
小学生でもわかる式変形で説明できます。
割られる数と割る数に同じ数をかけることで変形可能
割り算では、 $~6 \div 3=12 \div 6=2~$ のように、割られる数と割る数に同じ数をかけても商が同じになることをまずは説明します。
$~\displaystyle \frac{3}{4} \div \frac{2}{5}~$を計算するにあたって、割られる数と割る数に$ \displaystyle \frac{5}{2}~$ をかけて計算すると、
\begin{align*}
\frac{3}{4} \div \frac{2}{5} &= \left( \frac{3}{4} \times \frac{5}{2} \right) \div \left( \frac{2}{5} \times \frac{5}{2} \right) \\
\\
&=\left( \frac{3}{4} \times \frac{5}{2} \right) \div 1 \\
\\
&=\frac{3}{4} \times \frac{5}{2}
\end{align*}となるため、分数の割り算は逆数をかけることで表されることがわかります。
この計算を文字式で行えば、厳密な証明になりますが、正負の数は文字式が登場する前の単元のため、文字式は使用できません。
ご注意を。
0 で割ると答えは?
$~0 \div 6=0~$ですが、$~6 \div 0~$の答えはありません。
その理由を説明できますか?
確かめ算から説明できる
確かめ算の考え方を使うことで、簡単に説明できます。
まずは、$~6 \div 2=3 の確かめ算を復習しましょう。
3 \times 2=6
次に$~6 \div 0=\Box~$の確かめ算を考えます。
\Box \times 0=6
そして、$~\Box~$がいくつだったら式が成り立つかを考えます。
‥‥当然ありません。
これで$~6 \div 0~$の答えはないとわかりました。
同様の考え方で、$~0 \div 0~$の答えが無数にあることも言えます。
「指数」の由来
数字の右上につく小さな数字「指数」。
なぜこのような名前がついているのでしょうか?
index numberを訳した言葉
「指」という字は、「ゆび」ではなく、「さ(す)」から来ています。


ラテン語で”index”は「指し示すもの」という意味があり、「何回かけるか指示する数字」として、index numberと呼ばれました。
” index number “は中国にて指数と訳され、日本へと伝わっています。
現在の表記はデカルトによるもの
現在でこそ指数は右上に書きますが、それが定着する前は様々な方法で指数が表されました。
| 人物 | $~a^2~,~b^3~$の表記法 |
| フランソワ・ヴィエト(1591) | $a$.quad. , $b$.Cubum |
| アドリアン・ロマヌス(1593) | $a$(2) , $b$(3) |
| エリゴンヌ?(1634) | $a$2 , $b$3 |
| ヒューム?(1634) | $a^{Ⅱ}$ , $b^{Ⅲ}$ |
| ルネ・デカルト(1637) | $~a^2~,~b^3~$(現在の表記) |
ちなみに、指数を導入したフランスの数学者ニコラ・シュケ(Nicolas Chuquet , 1445-1500頃)は、$~4x~,~5x^2~$を$~.4.^{1}~~,~.5.^{2}~$という底$~x~$を省略する形で表記していました。
こうしてみると、いかにデカルトの表記法が有能かがわかりますね。
小学校で登場する指数
右かたに小さく書く指数ですが、$~2^3~$を$~23~$と書き間違える生徒がクラスに数人出てきます。
小学校の知識とつなげることで、そのようなミスを減らしたうえで、用語を覚えることまでできます。
面積や体積の単位とつなげる
小学校から使っている面積や体積の単位の復習をすることで、指数の表し方や読み方を導入しやすくなります。
具体例を挙げます。
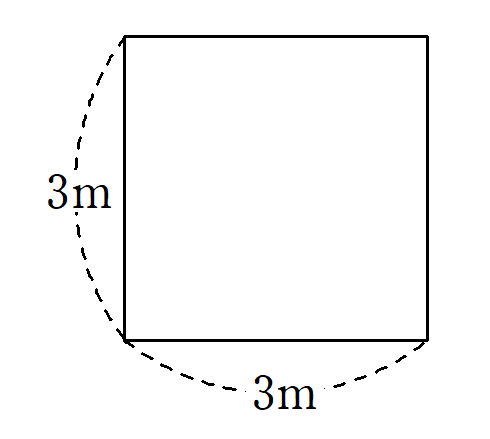
(1) 一辺$3$mの正方形の面積は、$3$m $\times$ $3$m $=9$m²
→ m を2回かけているから、m²(平方メートル)で、2乗のことを「平方」という。

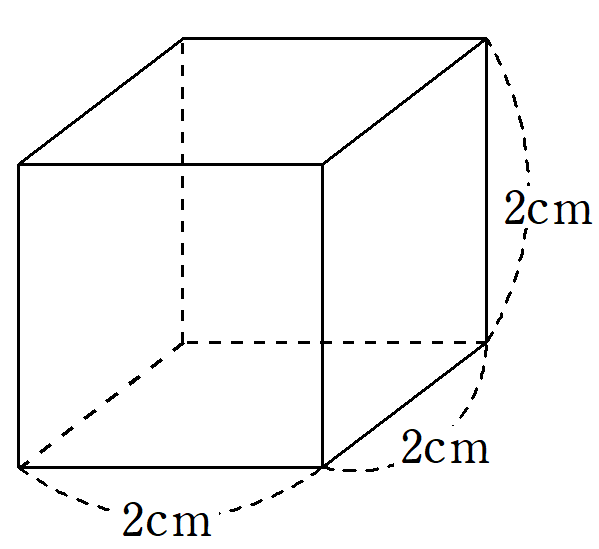
(2) 一辺$2$cmの立方体の体積は、$2$cm $\times$ $2$cm $\times$ $2$cm2cm=8cm³
→ cmを3回かけているから、cm³(立方センチメートル)で、3乗のことを「立方」という。

指数への抵抗感をなくしつつ、2乗や3乗の異称まで覚えられるのが利点です。
ただ、次の単元である文字式との整合性を気にするのであれば、cm は使わずに m だけを例示したほうが良いでしょう。
まとめ
中学数学の最初の単元である「正負の数」の小ネタについて紹介してきました。
この単元の授業の仕方によって、生徒のその後の数学への取り組み方が変わってきます。
「算数は苦手だったけど、数学の授業は面白い!」という生徒が増えるよう、授業準備を入念に行いましょう!



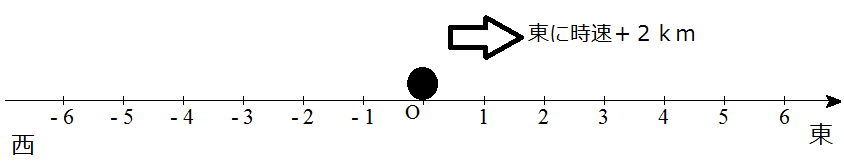

コメント