生徒が苦手意識を持ちやすい教科である数学。
そういった生徒たちの関心意欲を高めるために、生徒が主体的に取り組める数学的活動を授業の中で入れることが望ましいものの、
- 数学的活動は授業準備に時間がかかる(教員が忙しすぎる)
- カリキュラムの進行上、授業時数的に数学的活動をする余裕がない
といった理由から、例題→問題演習→例題→問題演習→‥‥となってしまいがちです。
しかし、そういった縛りの中でも、授業内に小ネタを挟むことで生徒の興味を惹いたり、数学が楽しいと思えるような授業を手軽に展開することができます。
この記事では、1回の授業の中で「1へぇー&1笑い」を実践し続けている現役数学教員が、中1の単元「文字と式」で使っている数学ネタを紹介!
準備不要で5分後の授業からでも使えます!!
この記事は随時更新していきます。
数学で使うアルファベット
「正負の数」の単元が終わり、いよいよ文字式に入っていきます。
英語でアルファベットを学んでいるため、その復習も兼ねて小文字のアルファベットをノートに書かせてみましょう。

この中から、数学でそのまま使えない(使いづらい)アルファベットを理由と共に答えてもらいます。
「b は$~6~$と似ているから、筆記体で書くこともある」というような例を出せば、あとは自然と挙手が起こります。
実際、以下のようなアルファベット表が完成。

各アルファベットについて、補足しておきます。
| アルファベット | 理由・補足 |
| b | $~6~$と似ている。筆記体で書かなくてもよいが、$~6~$と$~b~$の違いをハッキリと。 |
| g | $~9~$と似ている。筆記体で書かなくてもよいが、$~9~$と$~g~$の違いをハッキリと。 |
| i | $~1~$と混ざりやすい。ただ、中学数学では$~i~$が文字として登場することはほぼない。 |
| j | $~1~$と混ざりやすい。筆記体で書かなくてもよいが、しっかりと曲げよう。 |
| l | $~1~$と一緒。$~\ell~$で書こう。今の生徒は、リットルは”L”で習っている。 |
| o | $~0~$と一緒。計算で$~o~$が登場することはないが、大文字の$~O~$は関数分野で登場。 |
| q | $~9~$と似ている。筆記体で書くことを推奨。 |
| t | $~+~$と似ている。2画目をしっかりと曲げよう。 |
| x | $~\times~$と一緒。$~x~$または$~\xi~$のように書く。また、$~x~$については、一部の生徒に「シャネル」のマークで伝わる。 |
| y | 何かと混ざるわけではないが、筆記体で書くことが多い。 |
| z | $~2~$と混ざりやすい。角ばらせて書くか、2画目を真ん中に加えて書く。後者に関しては、一部の生徒に「かいけつゾロリ」の z で伝わる。 |
この取り組みをすることで、数学の文字式の掴みはバッチリです!
江戸時代の文字式
アルファベットが日本に伝わっていなかった江戸時代。
この時代では、文字式として特定の漢字を使っていました。
それが、甲・乙・丙・丁・戊・己・庚・辛・壬・癸の十干(十二支と合わせて、干支として使われる漢字)です。
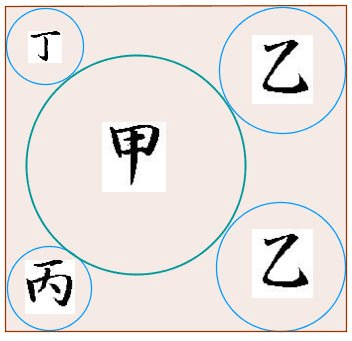
(出典:Greenland4, Public domain, via Wikimedia Commons)
実際、とある漢字圏では、「甲」=$~A~$、「乙」=$~B~$、‥‥、「癸」=$~J~$ と対応させているという情報もあります。
× の歴史
$~x \times x~$でわかる通り、$~x~$と$~\times~$(かける)は区別がつきづらいです。
そもそも乗算記号$~\times~$がいつ生まれたかというと、イギリスの数学者ウォリアム・オートレッド(William Oughtred , 1574-1660)の著書にまでさかのぼります。

(出典:Wenceslaus Hollar, Public domain, via Wikimedia Commons)
オートレッドは中世のかけ算の筆算方法をヒントとして、かけ算記号に”X”を採用しました。
$~37\times 61~$の筆算を次の図で行う。
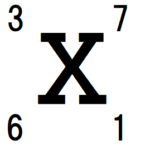
同じ桁どうしのかけ算とたすきがけの考え方により、
3 \times 6 \times 100+(3 \times 1 +7 \times 6) \times 10+ 7 \times 1=2257
と求められる。
数と数の間に、”X”を書いていたことから、オードレッドは”X”を使っています。
ただ、その直後の数学者ゴットフリート・ヴィルヘルム・ライプニッツ(Gottfried Wilhelm Leibniz , 1646-1716)が、$~x~$と$~\times~$が間違いやすいことから“$\cdot$”を好んで使ったため、ヨーロッパ本土では$~\times~$が流行りませんでした。
文字式で1を省略する理由
文字式の掛け算で引っかかりやすいのが、1の省略。
そんなときは、2つの式を並べます。
- $~1 \times 25=25~$
- $~-1 \times 25=-25~$
2つの式からもわかる通り、$~1~$は数字どうしの積でも省略(?)されていることがわかります。
ちなみに、$~0.1 \times 25=0.25~$とはならないので、$~0.1~$の$~1~$は省略してはいけないことも説明できますね。
π の由来と覚え方
中学に入ると、円周率が$~3.14~$から$~\pi~$へと変化します。
$~\pi~$はギリシャ語の$~\pi \epsilon \rho \iota \mu \epsilon \tau \rho \omicron \varsigma~$(円周)の頭文字をとったものです。

授業中に必ずと言っていいほど出てくる質問が、「先生はどのくらい円周率を言えますか?」という挑発。
関係もできてきた5,6月頃の授業内容なので、教員を試そうとする生徒が出てきます。
以下の語呂で小数第30位まで覚えられるため、事前に暗記して尊敬の念を集めましょう!
| 近似値 | 語呂(ひらがな) | 語呂(漢字) |
| 3.14159265 358979 3238462 643383279 | さんいしいこくにむこう さんごやくなく さんぷみやしろに むしさんざんやみになく | 産医師異国に向こう(かふ) 産後厄無く 産婦御社に 虫さんざん闇に鳴く |
「代入」「項」「係数」の漢字
文字式の分野では、今後の数学で何度も出てくる用語をたくさん学びます。
用語は漢字の他の読みと繋げてあげると、教科横断的で印象に残る暗記をさせることができます。
ここでは、以下の3つの用語について考えてみましょう。
| 用語 | 漢字の読みを利用した説明 |
| 代入 | 文字の代わりに数字を入れる。 |
| 項 | 「項目」でわかる通り、ひとまとまりの事柄をさらに細かく分類した一つ一つの事柄。式の項目。 |
| 係数 | 文字に係る数。文字に関係する数。 |
正負の数でも「項」は登場したものの、文字式になると項どうしが計算できない場合が出てくるため、「項目」という言葉がよりしっくり来るようになります。
余談ですが、「項」を「頂」と書く生徒が多いので、黒板に大きく「項」と書くことをおすすめします!
不等号と等号否定
不等式で登場する不等号。
似たような記号として、等号否定というものがあります。
「等しくない」を表すこれらの記号について、まとめてみました。
| 記号 | 読み方 | 意味 |
| $ < $ | 小なり | より小さい。未満。 |
| $\leqq$ | 小なりイコール | 以下。 |
| $ > $ | 大なり | より大きい。 |
| $\geqq$ | 大なりイコール | 以上。 |
| $neq$ | ノットイコール | 等しくない。 |
$~x \neq 5~$であれば、$~x~$は$~5~$より小さいか$~5~$より大きいということになります。
$~\neq~$は「不等号」と呼ばないことに注意が必要です。
「未満」と「以下」の漢字
不等号に関連して、よくある質問が「$~6~$未満に$~6~$は含みますか?」というもの。
そこで、説明の材料に使うのがまたまた漢字の読み。
| 用語 | 漢字の読みを利用した説明 |
| 未満 | 「未だ満たない」なので、$~6~$未満なら$~6~$にまだ到達していないことになる。よって$~6~$は含まない。 |
| 以下 | 「以て下」だとわかりづらいので、「3月10日を以て小学校を卒業した」を例にすると、3月10日に卒業したことになり、その日付を含んでいることがわかります。 |
「未満」=「より小さい」と暗記させるよりも効率が良く、言葉が持つ意味を感じさせられる内容となるでしょう。
まとめ
中学数学の2つめの単元である「文字と式」の小ネタについて紹介してきました。
文字の使用という算数と数学の違いを大きく感じさせるこの単元で、数学嫌いを作らないように楽しく授業をやりたいところ。
授業準備を入念に行いましょう!

コメント