
すべての三角形において、辺の長さとそれに対する角の大きさの大小関係には関係があります。当たり前に思えるこの関係について、証明や使用例まで含めて、ていねいに解説します。
- 辺が大きいほど、その辺に対する角は大きい
- 角が大きいほど、その角に対する辺は大きい
- この性質が必要となる正弦定理・余弦定理の問題
- この性質の証明
Ⅰ 三角形の辺に対する角の大小
Ⅰー① 定理
この記事で紹介するのは、すべての三角形で成り立つ、次のような性質です。
三角形において、大きい辺に対する角は、小さい辺に対する角より大きい。
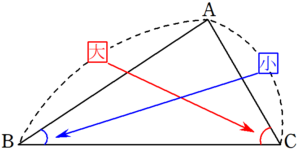

角の大きさの大小関係は、その角の向かいにある辺の大きさの大小関係と同じであることを主張しています。
Ⅰー② 例
有名な直角三角形を例に、確かめてみましょう。
$~30^{\circ}~, ~60^{\circ}~ , ~90^{\circ}~$の直角三角形
・大きい辺($AB=2$)に対する角($\angle C=90^{\circ}$)は、その辺より小さい辺($AC=1$)に対する角($\angle B=30^{\circ}$)より大きい。
AB > AC \Longrightarrow C > B


・大きい辺($AB=2$)に対する角($\angle C=90^{\circ}$)は、その辺より小さい辺($BC=\sqrt{3}$)に対する角($\angle B=60^{\circ}$)より大きい。
AB > BC \Longrightarrow C > A


要するに、辺の長さが大きいほど、それに対する角も大きくなるという、図を見れば当たり前の性質を主張している定理となります。
Ⅰー③ 証明
証明は、補助線の引き方を知っていればすごく簡単です。
$~AB > AC~$の$~\triangle ABC~$において、$~\angle C > \angle B~$を示す。


$~AD=AC~$となる点$~D~$を辺$~AB~$上にとる。


このとき、外角の性質から
\angle ADC=\angle B + \angle BCD
であるため、
\angle ADC > \angle B~~~~\cdots①
とわかる。


また、$~\triangle ADC~$は二等辺三角形となるので、
\angle ADC=\angle ACD ~~~~\cdots②
であり、$①$と$②$より、
\angle ACD > \angle B ~~~~\cdots③
がわかる。


角の位置関係より、
\angle C > \angle ACD ~~~~\cdots④
であるため、$③$と$④$より、
\angle C > \angle B
が示された。■
図形的に考えれば、理解が簡単な証明方法でした。
補助線の引き方を覚えておきましょう。
Ⅱ 三角形の角に対する辺の大小
Ⅱー① 定理
先ほどの定理の逆についても成り立ちます。
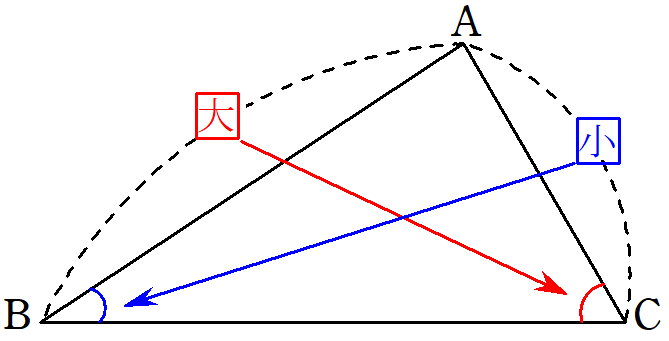
三角形において、大きい角に対する辺は、小さい角に対する辺より大きい。
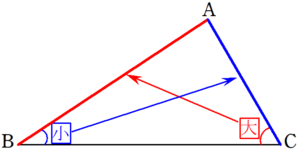

辺の大きさの大小関係は、その辺の向かいにある角の大きさの大小関係と同じであることを主張しています。
Ⅱー② 例
こちらについても有名な直角三角形を例に、確かめてみましょう。
$~45^{\circ}~, ~45^{\circ}~ , ~90^{\circ}~$の直角三角形
・大きい角($\angle C=90^{\circ}$)に対する辺($AB=2$)は、その角より小さい角($\angle B=45^{\circ}$)に対する辺($AC=1)より大きい。
C > B \Longrightarrow AB > AC
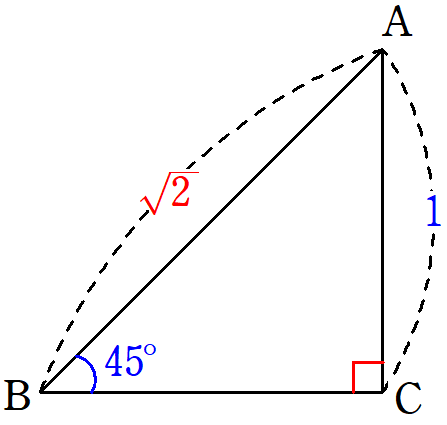

角の大きさが大きいほど、それに対する辺の大きさも大きくなるということを主張している定理となります。
Ⅱー③ 証明
命題が真だからと言って、その逆も真とは限らないので、きちんと証明をしてあげる必要があります。
こちらも補助線が重要です。
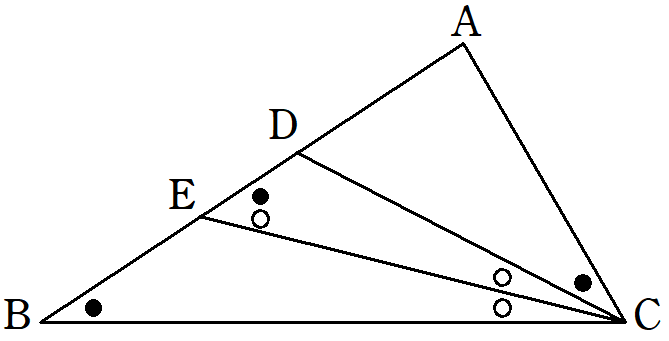
$~\angle C > \angle B~$ の $~\triangle ABC~$ において、 $~AB > AC~$ を示す。
まず、$~\angle ACD = \angle B~$となる点 $~D~$ を辺 $~AB~$ 上にとる。
さらに、$~\angle DCB~$の二等分線と辺$~AB~$の交点を$~E~$とする。
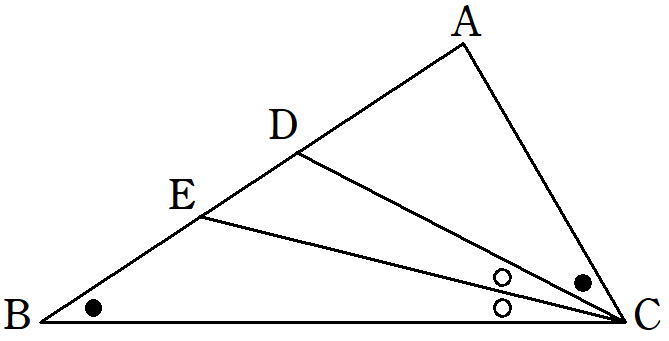

このとき、外角の性質から
\angle AEC=\angle B + \angle ECB ~~~~\cdots⑤
となる。

$⑤$を仮定によって変形していくと、
\begin{align*}
\angle AEC&=\angle ACD + \angle ECD \\
&=\angle ACE
\end{align*}となり、$~\triangle AEC~$は二等辺三角形であることがわかるため、
AE=AC ~~~~\cdots⑥
がわかる。
また、$~E~$の位置関係より、
AB > AE~~~~\cdots⑦
であり、$⑥$と$⑦$を合わせて
AB > AC
が示された。■
補助線の数こそ増えたものの、使う図形の本質は同じでした。
Ⅲ 三角形の辺と角の関係の活用例
この定理とセットで登場するのは、三角不等式です。
こちらについては、別記事で紹介しています。


三角不等式以外で使うことが多いのは、正弦定理・余弦定理です。
こんな例題を考えてみましょう。
$~\triangle ABC~$において、$~a=\sqrt{6}~,~b=\sqrt{3}-1~,~C=45^{\circ}~$のとき、残りの辺の長さと角の大きさを求めよ。
正弦定理を使うのか、余弦定理を使うのかの判断が難しい問題です。
Ⅲ-① 例題の解説(前半部分)


まずは、余弦定理によって、$~c~$を求める。
\begin{align*}
c^2&=(\sqrt{6})^2+(\sqrt{3}-1)^2-2\cdot \sqrt{6} \cdot (\sqrt{3}-1) \cdot \cos{45^{\circ}} \\
&=6+3-2\sqrt{3}+1-2\sqrt{6}(\sqrt{3}-1)\cdot \frac{1}{\sqrt{2}} \\
&=10-2\sqrt{3}-2\sqrt{3}(\sqrt{3}-1) \\
&=10-2\sqrt{3}-6+2\sqrt{3} \\
&=4
\end{align*}となるので、$~c > 0~$より、$~c=2~$とわかる。
ここまでは迷いようが無いです。


Ⅲ-② 例題の解説(後半部分・余弦定理の使用)
この後、教科書では余弦定理を使って、以下のように解いています。
余弦定理を変形した式より、
\begin{align*}
\cos{A}&=\frac{2^2+(\sqrt{3}-1)^2-(\sqrt{6})^2}{2\cdot 2 \cdot (\sqrt{3}-1)} \\
\\
&=\frac{4+3-2\sqrt{3}+1-6}{4(\sqrt{3}-1)} \\
\\
&=\frac{2-2\sqrt{3}}{4(\sqrt{3}-1)} \\
\\
&=\frac{-2(\sqrt{3}-1)}{4(\sqrt{3}-1)} \\
\\
&=-\frac{1}{2} \\
\end{align*}なので、$~A=120^{\circ}~$。
よって、$~C=180^{\circ}- 120^{\circ}-45^{\circ}=15^{\circ}~$も求まる。
確実に求まるのはこの方法ですが、計算が複雑。
特に$~(\sqrt{3}-1)~$で約分するところは、慣れていないと難しいですよね。
Ⅲ-③ 例題の解説(後半部分・正弦定理の使用)
そこで$~\sqrt{3}-1~$を避けるために、正弦定理を使うという手もあります。
正弦定理より
\begin{align*}
\frac{2}{\sin{45^{\circ}}}&=\frac{\sqrt{6}}{\sin{A}} \\
\\
2\sin{A}&=\sqrt{6}\sin{45^{\circ}} \\
\\
\sin{A}&=\frac{\sqrt{6}}{2}\cdot \frac{1}{\sqrt{2}} \\
\\
\sin{A}&=\frac{\sqrt{3}}{2}
\end{align*}なので、$~A=60^{\circ}~,~120^{\circ}~$。
正弦定理の場合、求まるのは$~\sin{}~$の値なので、多くの場合は解が2つ出ます。
Ⅲ-④ 例題の解説(後半部分・正弦定理の注意点)
正弦定理を使った場合の解の絞り込みに使えるのが、今回の「三角形の辺と角の関係」です。
角の大きさが大きいほど、それに対する辺の大きさも大きくなることから、 $~\sin{A}=\displaystyle \frac{\sqrt{3}}{2}~$を満たす$~A~$を、次のように問題を解き切ることができます。
$~A=60^{\circ}~$のとき、
$~B=75^{\circ}~$となり、$~B > A > C~$である。
このとき、$~b > a > c~$となる必要があるが、$~b=\sqrt{3}-1~,~a=\sqrt{6}~,~c=2~$で、$~a > c > b~$となっているため不適。


$~A=120^{\circ}~$のとき、
$~B=15^{\circ}~$となり、$~A > C > B~$である。
このとき、$~a > c > b~$となる必要があり、満たしている。


以上より、$~A=120^{\circ}~$であり、$~B=15^{\circ}~$となる。
もちろん、2つとも不適にならないという問題もありますので、ご注意ください。



図を正確に書くって大切だね。



うん。長さもある程度正確に書けば、一目で不適かどうかがわかるよ。
実際は、今回の関係を使って、不適の理由付けをしてあげよう。
コメント