飛んでいる矢は止まっている
この不思議な表現は、古代ギリシャの哲学者ゼノンが提起した一連のパラドックスの中の一つです。
この記事では、
- このパラドックスがどのようにして提起されたのか
- なぜ飛んでいる矢が止まっているという説明ができるのか
- パラドックスをどのように解決すればよいのか
という疑問を解消するため、飛んでいる矢のパラドックスを具体例を用いて、現役数学教員がわかりやすく解説しています。
このパラドックスの本質は「0に近づける」と「0に等しい」の違いにあり、その考え方は17世紀の微分の誕生にも関連しているのです!
飛んでいる矢のパラドックスとは?
飛んでいる矢は当然ながら動いています。

しかし、今回の飛んでいる矢のパラドックスによれば、飛んでいる矢は止まっていることが証明できてしまうのです!

哲学者ゼノンが提起したパラドックスの1つ
紀元前5世紀頃の哲学者ゼノン(Zeno , B.C.490頃-B.C.430頃)は、当時の数学を牽引していたミレトス学派の考え方に疑問を呈するためにパラドックスをいくつか提起しました。
その中の1つが今回の「飛んでいる矢のパラドックス」です。

(出典:Jan de Bisschop, CC0, via Wikimedia Commons)
 ゼノン
ゼノンミレトス派は時間の最小単位を瞬間と言っているけど、本当かな?
飛んでいる矢は止まっているという矛盾を示した
では、飛んでいる矢のパラドックスの中身の説明に入ります。
ゼノンの説明は以下のようなものでした。
移動するものは今において常にそれ自身と等しいものに対応しているならば、移動する矢は動かない。
「移動するもの」が「飛んでいる矢」を表しており、瞬間を切り取れば矢は動いていないのだから、その瞬間の積み重ねでできた時間の中で矢が動くことはないと主張しています。



はい、ミレトス派論破~。
どんなスピードで矢が飛んでいようとも写真を撮れば、そこに写された矢は止まっています。
それを繰り返したところで、矢は止まった状態のままということです。
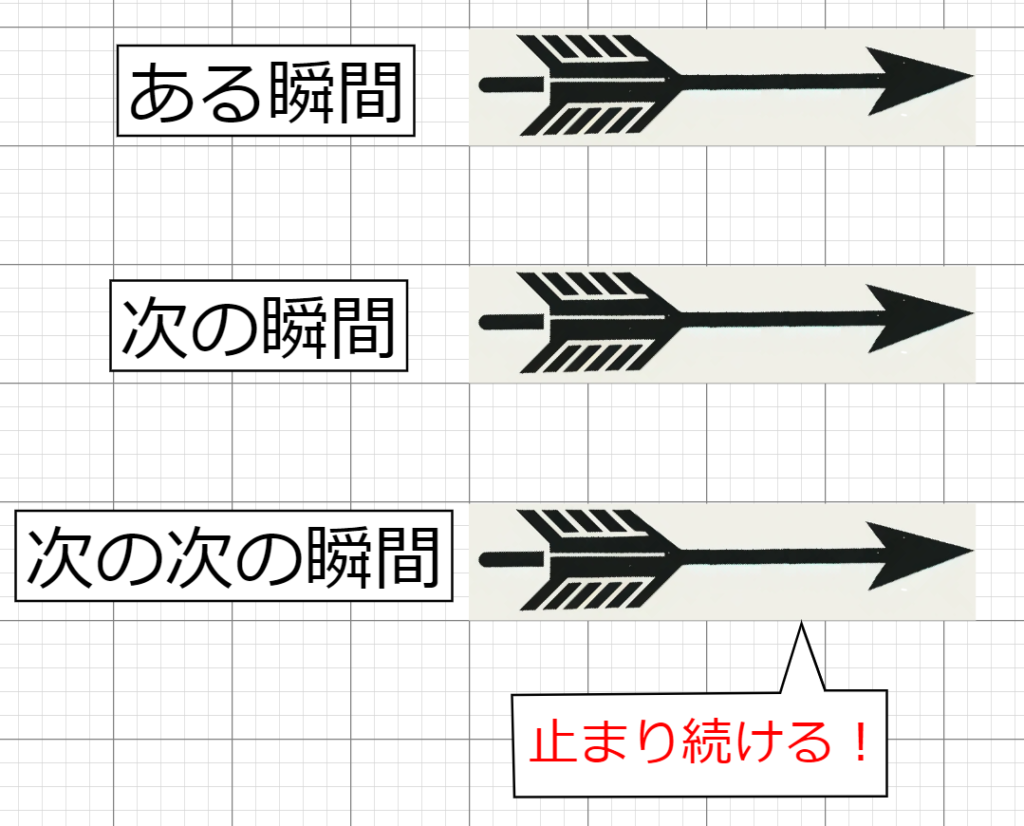

秒速60mの矢が秒速0mになる
もう少し詳しく、具体的な数値を使って考えてみます。
秒速$~60~$mで左から右に飛ぶ矢を考える。
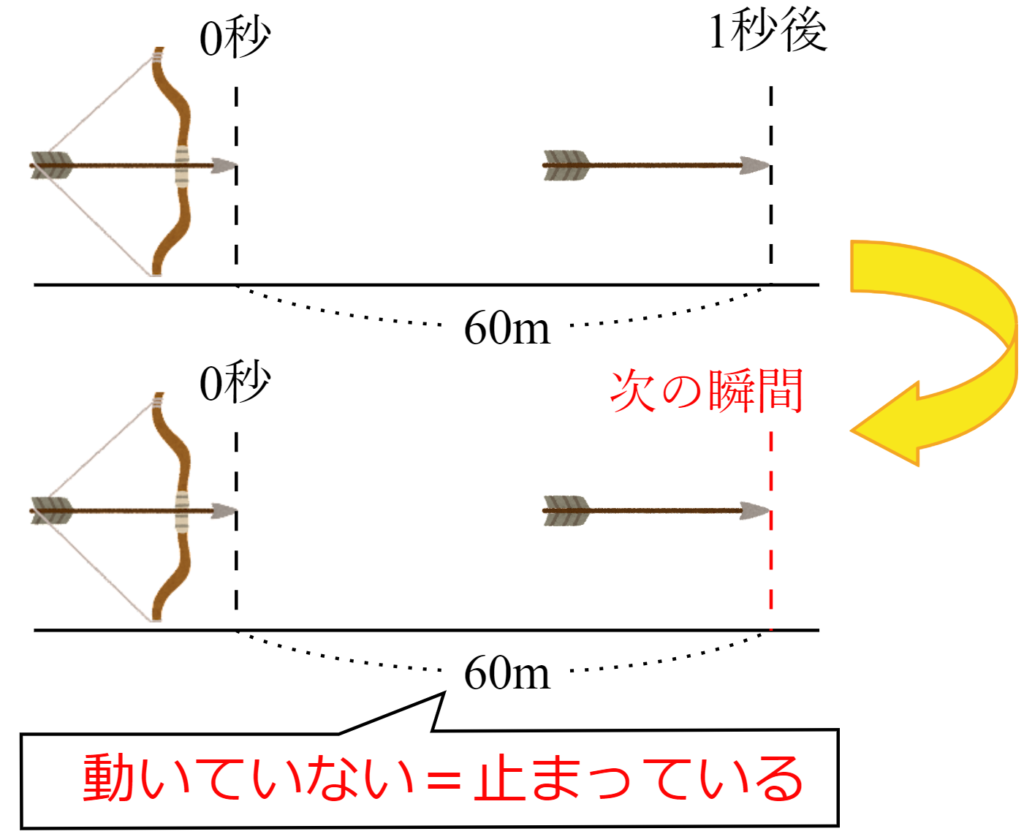

$~1~$秒後という瞬間において、矢は$~60~$m地点を飛んでいる。
次の瞬間も$~60~$m地点を飛んでいるため、この間の移動距離は$~0m~$。
よって、速さは秒速$~0~$mである。
秒速$~60~$mで飛んでいることを仮定したはずの矢が、速さ$~0~$(止まっている状態)になってしまいました。
この理論は$~1~$秒後に限らず、どの瞬間においても適用されるため、飛んでいる矢は止まっていると結論づけられるのです。
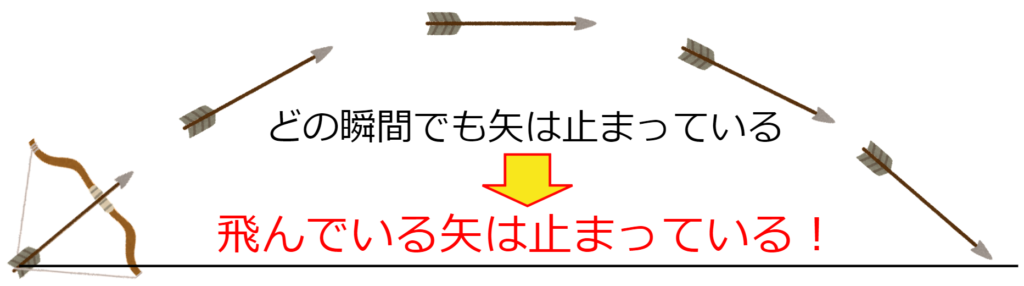

飛んでいる矢のパラドックスはどう解決されるのか?
ゼノンの主張は一見すると合っているようにも思えますが、現実とのズレはどこにあるのでしょうか。
先ほどの飛んでいる矢のパラドックスの具体例を使って、そのズレを考えてみましょう。
パラドックスの原因は 0÷0
発射されてから$~x~$秒後に、$~y~$m 離れた地点を矢が進んでいるものとすると、$~x~$と$~y~$の関係は$~y=60x~$で表されます。
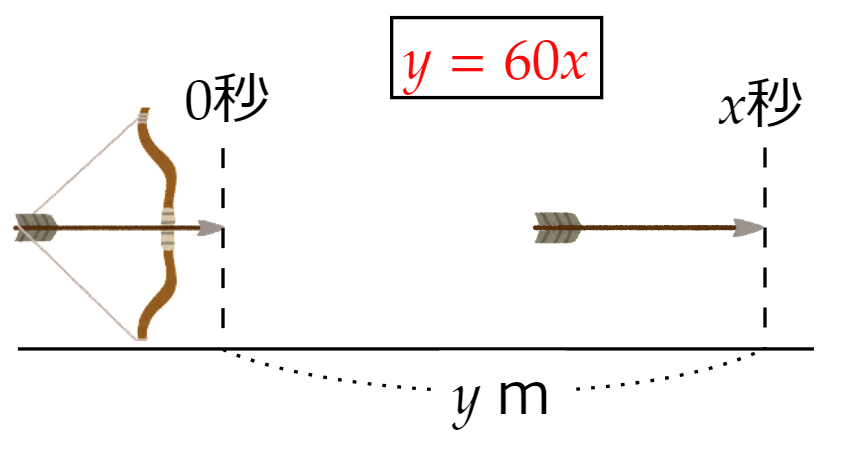

ゼノンの主張を、$~x~$と$~y~$で対応させると次の関係となります。
| 1秒後のある瞬間 | 次の瞬間 | |
| 時間$~x~$(秒) | $~1~$ | $~1~$ |
| 距離$~y~$(m) | $~60~$ | $~60~$ |
この間の速さは、
\frac{この間に進んだ距離}{この間に進んだ時間}なので、
\frac{60−60}{1−1}=\frac{0}{0}=0 \div 0となり、数学界のタブーである「0を割る」ことをしてしまっているのです。
無限小を$~0~$と誤認識してしまったことが、タブーを犯した原因となっています。



ちなみに$~0\div 0~$は不定解(答えは何でも成り立つ)。
そのため、$~0\div 0=0~$とは限りません。
微分と同様の考え方で解決できる
実際は、「次の瞬間」という言葉が限りなく0秒に近い時間を表すため、微小な時間$~t~$を用いて次のように表すのが正しい解釈です。
| 1秒後のある瞬間 | 次の瞬間 | |
| 時間$~x~$(秒) | $~1~$ | $~1+t~$ |
| 距離$~y~$(m) | $~60~$ | $~60(1+t)~$ |
この$~t~$を限りなく$~0~$に近づけたときの速さは、
\begin{align*}
\lim_{t \to 0}\frac{60(1+t)-60}{(1+t)-1}&=\lim_{t \to 0}\frac{60t}{t} \\
\\
&=\lim_{t \to 0}60 \\
&=60
\end{align*}であり、元々の設定であった秒速$~60~$mと等しくなりました。
この「限りなく$~0~$に近づける」というのは微分と同様の考え方であり、17世紀のニュートンやライプニッツといった数学者たちによって確立されました。
まとめ:「0に近づける」と「0に等しい」は別物
「飛んでいる矢は止まっている」というパラドックスについて解説をしてきました。
- 古代ギリシャの哲学者ゼノンが、ミレトス学派に対抗するために提起した。
- 瞬間から次の瞬間を考えるときに、$~0~$秒後を考えたことがパラドックスの原因。
- 「$~0~$に近づける」という、微分と同様に考えることで、パラドックスは解決する。



$~0~$に近づけることと、$~0~$にすることは似ているようで違うんだ~。



極限($~\lim~$)の重要性がわかるパラドックスだったね。
参考文献
- 『カッツ 数学の歴史』,pp.68-69.
- 『メルツバッハ&ボイヤー数学の歴史Ⅰー数学の萌芽から17世紀前期までー』,pp.72-74.
- 『数学の流れ30講(上)ー16世紀までー』,pp.28-31.
- 『数学の歴史物語』,pp.46-47.
- 『世界数学者事典』,pp.252-253.
- 『ギリシャ数学史』,pp.154-155.
- 『アキレスとカメーパラドックスの考察ー』,pp88-89.

コメント