1674年、ゴットフリート・ライプニッツによって示された級数です。円周率の $~\displaystyle \frac{1}{4}~$ の値が単純な分数のたし算引き算によって表されます。17世紀末から18世紀初頭、この級数を利用して円周率の近似値計算が行われました。
①ライプニッツ級数
②証明
③円周率の近似計算
①ライプニッツ級数
ライプニッツ級数とは、1674年、ゴットフリート・ライプニッツによって示された級数です。
まずはどのような級数なのかを見てみます。
次のような級数をライプニッツ級数という。
\begin{equation}
\displaystyle \sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}=\frac{\pi}{4}
\end{equation}
わかりやすくするために、左辺を書き換えると、
\begin{equation}
\displaystyle 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots
\end{equation}
となります。分子が1、分母が奇数の分数を交互に加減していくという意味です。
この操作を無限に行うと、円周率の $~\displaystyle \frac{1}{4}~$ になるというのは不思議ですね。
※このサイトでは、ライプニッツ級数を一般化したものをグレゴリー級数としていますが、まとめて「グレゴリー・ライプニッツ級数」と呼んだり、諸説あるようです。
②証明
では、証明に入ります。高校数学の知識だけでできます。一応。
初項 $~1~$ 、公比 $~-x^2(0 \le x <1)~$ の無限等比級数を考えると、|公比|$<1~$ より、次のような関係式が表せる。
\begin{equation}
\displaystyle 1-x^2+x^4-x^6+\cdots=\frac{1}{1-(-x^2)}=\frac{1}{1+x^2}
\end{equation}
ここで、 $~x:0 \to 1~$ について、両辺積分をとると、
\begin{equation}
\displaystyle \int_{0}^{1}( 1-x^2+x^4-x^6+\cdots)dx=\int_{0}^{1}\frac{1}{1+x^2}dx ・・(*)
\end{equation}
であり、左辺と右辺それぞれを計算する。
左辺について計算していくと、
\begin{align}
\displaystyle (左辺)&=\int_{0}^{1}( 1-x^2+x^4-x^6+\cdots)dx \\
\\
&=\left[ x-\frac{1}{3}x^3+\frac{1}{5}x^5-\frac{1}{7}x^7+\cdots \right]_{0}^{1} \\
\\
&=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots
\end{align}
となる。
右辺に関しては、 $~x=\tan{\theta}~$ と置換することで、
$~ x:0 \to 1 ~$ が $~\theta :0 \to \displaystyle \frac{\pi}{4} ~$ となり、 $~ \displaystyle dx=\frac{1}{\cos^{2} \theta}d \theta ~$ となるため、
\begin{align}
\displaystyle (右辺)&=\int_{0}^{1}\frac{1}{1+x^2}dx \\
\\
&=\int_{0}^{\frac{\pi}{4}}\frac{1}{1+\tan^{2}\theta}\cdot \frac{1}{\cos^{2} \theta}d \theta \\
\\
&=\int_{0}^{\frac{\pi}{4}} \cos^{2}\theta \cdot \frac{1}{\cos^{2} \theta}d \theta \\
\\
&=\int_{0}^{\frac{\pi}{4}}d \theta \\
\\
&=[\theta]_{0}^{\frac{\pi}{4}} \\
\\
&=\frac{\pi}{4}
\end{align}
と右辺も求まった。
左辺と右辺の計算結果を元の等式$(*)$に代入することで、
\begin{equation}
\displaystyle 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots = \frac{\pi}{4}
\end{equation}
となり、ライプニッツ級数の値が求まった。 $~\blacksquare$
初項 $~1~$ 、公比 $~-x^2(0 \le x <1)~$ の無限等比級数を考えると、|公比|$<1~$ より、次のような関係式が表せる。
\begin{align}
&\displaystyle 1-x^2+x^4-x^6+\cdots \\
\\
&=\frac{1}{1-(-x^2)} \\
\\
&=\frac{1}{1+x^2}
\end{align}
ここで、 $~x:0 \to 1~$ について、両辺積分をとると、
\begin{equation}
\displaystyle \int_{0}^{1}( 1-x^2+x^4-\cdots)dx=\int_{0}^{1}\frac{1}{1+x^2}dx
\end{equation}
となる。・・・(*)
(*)の左辺と右辺それぞれを計算する。
左辺について計算していくと、
\begin{align}
\displaystyle (左辺)&=\int_{0}^{1}( 1-x^2+x^4-x^6+\cdots)dx \\
\\
&=\left[ x-\frac{1}{3}x^3+\frac{1}{5}x^5-\frac{1}{7}x^7+\cdots \right]_{0}^{1} \\
\\
&=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots
\end{align}
となる。
右辺に関しては、 $~x=\tan{\theta}~$ と置換することで、
$~ x:0 \to 1 ~$ が $~\theta :0 \to \displaystyle \frac{\pi}{4} ~$ となり、 $~ \displaystyle dx=\frac{1}{\cos^{2} \theta}d \theta ~$ となるため、
\begin{align}
\displaystyle (右辺)&=\int_{0}^{1}\frac{1}{1+x^2}dx \\
\\
&=\int_{0}^{\frac{\pi}{4}}\frac{1}{1+\tan^{2}\theta}\cdot \frac{1}{\cos^{2} \theta}d \theta \\
\\
&=\int_{0}^{\frac{\pi}{4}} \cos^{2}\theta \cdot \frac{1}{\cos^{2} \theta}d \theta \\
\\
&=\int_{0}^{\frac{\pi}{4}}d \theta \\
\\
&=[\theta]_{0}^{\frac{\pi}{4}} \\
\\
&=\frac{\pi}{4}
\end{align}
となる。
左辺と右辺の計算結果を元の等式(*)に代入することで、
\begin{equation}
\displaystyle 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots = \frac{\pi}{4}
\end{equation}
となり、ライプニッツ級数の値が求まった。 $~\blacksquare$
左辺の積分は数学Ⅱでもできる単純な積分、右辺の積分は置換積分の代表的な形の1つです。
※ $~0 \le x <1~$ という定義域で無限等比級数の和を考えているため、正確には $~x:0 \to 1-\epsilon~$ で積分を考え、 $~\epsilon \to 0+~$ という極限の操作をしてあげる必要があります。(広義積分)
③円周率の近似計算
ライプニッツ級数は、左辺が整数分数のたし算引き算(永遠に)、右辺は円周率の $~\displaystyle \frac{1}{4}~$ であるため、左辺を無限に計算することで、円周率の値を求めることができます。
では、どれくらいの精度なのでしょうか?計算してみました。
円周率$\pi~$ は、ライプニッツ級数を利用して次のように表せる。
\begin{equation}
\displaystyle \pi=4\cdot \lim_{n \to \infty}\sum_{k=1}^{n}\frac{(-1)^{k+1}}{2k-1}
\end{equation}
この式は先ほどのライプニッツ級数の式を $~\pi~$ について解き、右辺を少し変形したものです。 $~n~$ を1ずつ増やして、 $~\pi~$ の値を求めてみます。
\begin{align}
\pi&=4 \cdot 1 \\
&=4
\end{align}
$~n=1~$ の誤差は0.85840734
3.14を超えたところからのスタートです。
\begin{align}
\pi&=4\left( 1-\frac{1}{3} \right) \\
&=4\cdot \frac{2}{3} \\
&=2.666666666
\end{align}
$~n=2~$ の誤差は0.47492598
今度は3.14よりも小さくなってしまいました。でも一気に近づいた!
\begin{align}
\pi&=4\left(1-\frac{1}{3}+\frac{1}{5}\right) \\
&=4\cdot \frac{13}{15} \\
&=3.4666666666
\end{align}
$~n=3~$ の誤差は0.32507401
また3.14を超えた!でも、この調子で誤差を小さくしてほしい!
\begin{align}
\pi&=4\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\right) \\
&=4\cdot \frac{76}{105} \\
&=2.895238
\end{align}
$~n=4~$ の誤差は0.24635455
3.14の周りを近づきながら振動していますね。
少しとばします。
\begin{align}
\pi&=4\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots-\frac{1}{19}\right) \\
&=3.04183961
\end{align}
$~n=10~$ の誤差は0.09975303
おー。
思い切って1000まで計算すると・・・
\begin{align}
\pi&=4\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots-\frac{1}{1999}\right) \\
&=3.14059265
\end{align}
$~n=1000~$ の誤差は0.00100000
なんか、妙に一致しているが、小数第3位が違う・・。
最後の最後、10000!
\begin{align}
\pi&=4\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots-\frac{1}{19999}\right) \\
&=3.14149265
\end{align}
$~n=10000~$ の誤差は0.00010000
これまた妙に一致しているが、小数第4位が違う・・。
分母が奇数なので手計算だと通分が大変です。そして、収束速度もそんなに速くない・・。
一応、 $~n=100~$ までの様子をグラフにしたものを載せておきます。
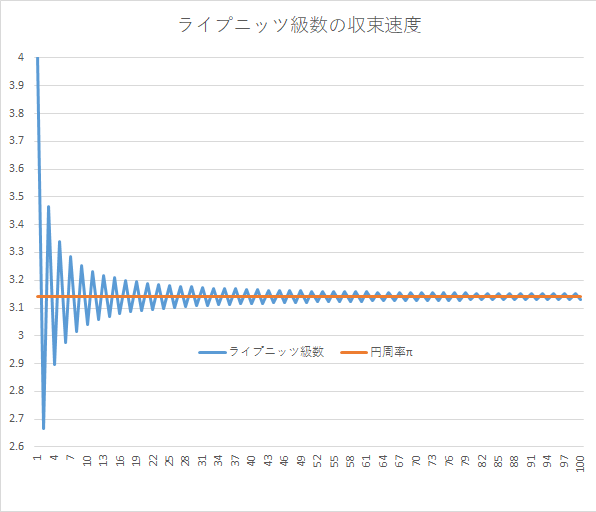
振動がすごいですね。
ウォリスの公式同様、円周率を近似するという観点からライプニッツ級数について触れました。ただ、収束速度が遅いので、実際の円周率の近似計算では使えなさそうです。

☆参考文献等
・「受験の月 積分漸化式の応用②」,<http://examist.jp/mathematics/integration-expression/mercator-leibniz/> 2017年3月21日アクセス
・「Wikipedia」,<https://ja.wikipedia.org/wiki/%E3%83%A9%E3%82%A4%E3%83%97%E3%83%8B%E3%83%83%E3%83%84%E3%81%AE%E5%85%AC%E5%BC%8F> 2017年3月21日アクセス
コメント
コメント一覧 (6件)
質問です
証明のところで、xの定義域を[0,1)にされていましたが、なぜそう仮定するのでしょうか(自分は高校3年なのですが、もし高3でも理解できそうなのであれば教えていただきたいです。)
あとその定義域で考えるのに積分区間を0→1にしても問題ないんですか??
よろしくお願いします。
ご質問ありがとうございます。
無限等比級数を収束させるために、公比の絶対値が 1 より小さくないといけないので、 \( x\) の定義域を 1 より小さくしています。
収束する上では \(x=0\) でも問題ないので、 \( [0,1)\) としています。
積分区間に関しては、証明後の※にも書いたのですが、本来は \(\displaystyle \lim_{\epsilon \to 0+} \int_{0}^{1-\epsilon}\) で計算してあげないといけないのですが、高校数学の知識だけということで、そこの厳密性を無視しています。
先生、早速のご返信ありがとうございます!
先生の記事は高校生にもわかりやすくて、とても勉強になっています。:
これからも、:よろしくお願いいたします!!
嬉しいコメントありがとうございます。
今日は記事の更新日でしたので、早速メルカトル級数について書いてみました。
ライプニッツ級数のときと同様のレイアウトですが・・・
どうぞご覧ください。
メルカトル級数
先生、こんにちは!
ライプニッツ級数の記事、とてもおもしろかったです!
メルカトル級数や調和級数のお話もつくっていただけるとうれしいです!
よろしくお願いいたします!!
ライプニッツ級数の記事、読んでいただきありがとうございます。
メルカトル級数で\(~\log{2}~\)の近似値をひたすら求めてみるのも面白そうですね!!
今週の木曜日の更新日のネタにさせていただきます。
調和級数に関してもひたすら計算して、発散がいかに遅いのかを調べてみます(笑)
今後ともどうぞよろしくお願いします。