
折り紙を使うと、定規やコンパスが無くても正三角形が作れます。
正三角形の折り方とその理由を解説します。
- 折り紙における正三角形の折り方
- 正三角形が折れる理由
Ⅰ 正三角形の作り方
折り紙を1枚用意して、是非実際に折ってみてください。
1.十字の折り目をつける。
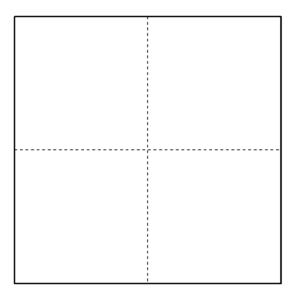

2.頂点が折り目に重なるように2方向から折る。
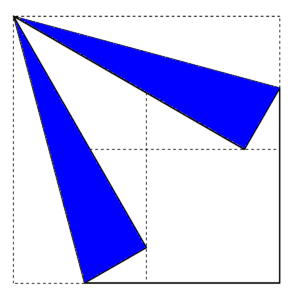

3.下のように折れば、正三角形の出来上がり!
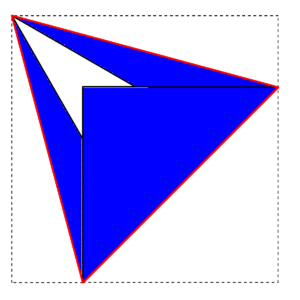

このようにすぐ正三角形が出来上がります。
ただ、実際に折ってみると2つめの手順のところが若干折りづらいですね。
Ⅱ 正三角形になる理由
あの折り方でなぜ正三角形となるのかを考えてみましょう。
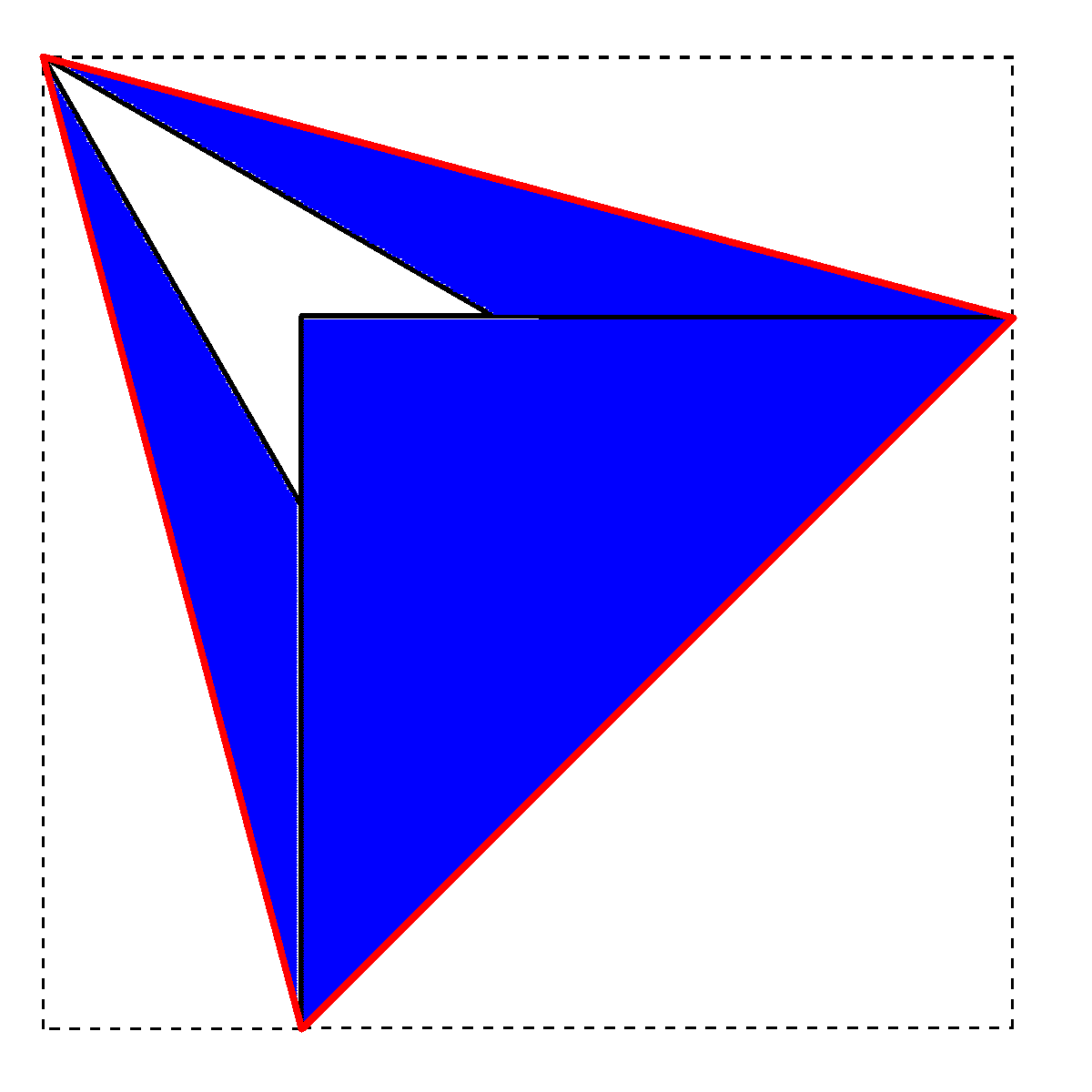
図4のように、1つの頂点を、十字の折り目に向けて折ることを考える。
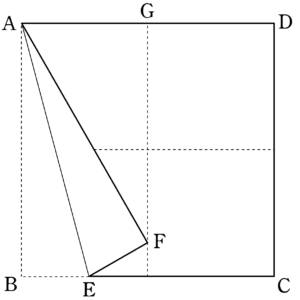

図5の$~\triangle FGA~$と$~\triangle FGD~$について、
- 半分に折っているため、$~AG=DG~$
- 折り目は$~180^{\circ}~$を二等分しているので、$~\angle FGA=\angle FGD~$
- 共通なので、$~FG=FG~$
二辺夾角相等から$~\triangle FGA \equiv \triangle FGD~$。
よって、対応する辺から、
\begin{equation*}
FA=FD ~~~\cdots ①
\end{equation*}である。
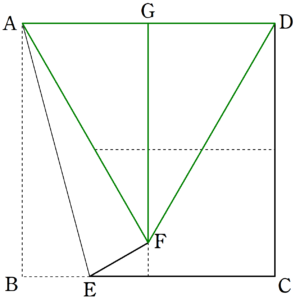

また、もともとは同じ辺であることから、
\begin{equation*}
AB=FA ~~~\cdots ②
\end{equation*}であり、正方形の辺の長さから、
\begin{equation*}
AB=AD ~~~\cdots ③
\end{equation*}
となる。
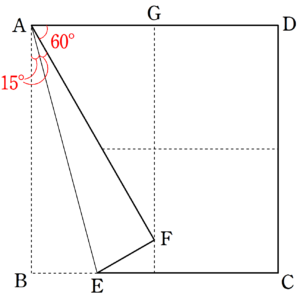
$①$~$③$から、$~FA=FD=AD~$で、$~\triangle FAD~$は正三角形となる。
そのため、$~\angle FAD=60^{\circ}~$であり、折り目の性質から
\begin{equation*}
\angle BAE=15^{\circ} ~~~\cdots ④
\end{equation*}が求まる。

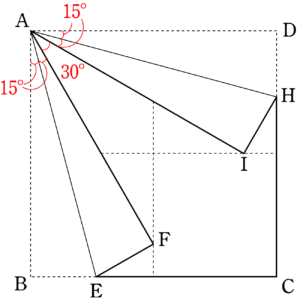
同様に、
\begin{equation*}
\angle DAH=15^{\circ} ~~~\cdots ⑤
\end{equation*}も求まる。

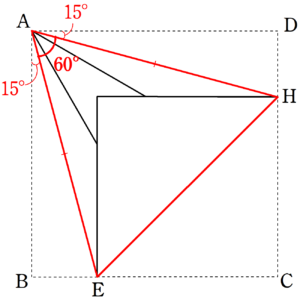
よって、$~\triangle AEH~$を考えると、$④$と$⑤$より、$~\angle EAH=60^{\circ}~$を満たす。
また、$~AE=AH~$となるため、$~\triangle AEH~$は正三角形であることが示された。■

ちなみに、図5で三平方の定理を使えば、合同を使わずに$~\angle FAG=60^{\circ}~$がすぐわかります。
今回は、中2までの知識でわかる方法で証明を行いました。



これ、きれいに折れなくない?



折りにくいのは重々承知。
でも、すべての角が90°の正方形から、正三角形が折れるってすごくない?
コメント