階差数列型では、$\sum$の計算結果が、$n=1~$でも成り立つかどうかを最後に確かめます。なぜこれが必要なのか？ また、 $n=1~$ で成り立たない例はあるのかを解説します。
- 階差数列型で、$n=1~$と$~n \geqq 2~$で分ける理由は$~\sum~$の公式にある！
- $~n=1~$の確かめでは、ほぼ100%成立する！
- $~n=1~$で成り立たない例は、$n=1$で場合分けされているとき。
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊
重刷、ブログ累計200万PV達成 - 行間がなくなるほど丁寧な式変形で執筆中
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊は発売1ヶ月で即重刷
- 当数学史ブログは累計200万PV達成
- 行間がなくなるほど丁寧な式変形で記事を執筆
『世界を変えた数学史図鑑』『教養としての数学史』好評発売中！
丸善日本橋店の2025年ベストセラー（理工書部門）に選ばれました！
（理工書部門）に選ばれました！
Ⅰ n=1 を確かめる理由
なぜ\(~n=1~\)で成り立つかどうかの確認をするのでしょうか？
その理由は簡単で、$~\{a_n\}~$の階差数列を$~\{b_n\}~$としたとき、
a_n=a_1+\sum_{k=1}^{n-1}b_k~~~\cdots ①と表されます。
ここに$~n=1~$を代入すると、
a_1=a_1+\sum_{k=1}^{0}b_k~~~\cdots ②となります。
ここで、困るのが$~\displaystyle \sum_{k=1}^{0}b_k~$の部分。
$~k=1~$から$~k=0~$までの$~b_k~$の和！？
と困るわけです。
そこで、実際の式では$~n \geqq 2~$という制約をつけて$①$の右辺を計算し、最後に$~n=1~$のときにも等式が成り立つかを確かめる必要があるのです。
よくある問題の例を１つ挙げてみます。
$~1 , 2 , 4 , 7 , 11 , 16 , \cdots~$で与えられている数列$~\{a_n\}~$を求める。
この数列の階差数列$~\{b_n\}~$を調べると、
1 \xrightarrow{b_1=1} 2 \xrightarrow{b_2=2} 4 \xrightarrow{b_3=3} 7 \xrightarrow{b_4=4} 11 \xrightarrow{b_5=5} 16 \cdotsであり、$~b_n=n~$と表せるので、$~n \geqq 2~$のとき、
\begin{align*}
a_n&=a_1+\sum_{k=1}^{n-1}b_k \\
\\
&=1+\sum_{k=1}^{n-1}k \\
\\
&=1+\frac{1}{2}n(n-1) \\
\\
&=\frac{1}{2}n^2-\frac{1}{2}n+1~~~\cdots ③
\end{align*}となる。
また、$~n = 1~$を$③$に代入すると、
\begin{align*}
a_1&=\frac{1}{2}\cdot 1^2-\frac{1}{2}\cdot 1+1 \\
\\
&=\frac{1}{2}-\frac{1}{2}+1 \\
\\
&=1
\end{align*}であるため、 $~n = 1~$のときにも成り立つ。
したがって、一般項は
a_n=\frac{1}{2}n^2-\frac{1}{2}n+1と求まった。
学んだ直後は、$~n=1~$の確認が割と新鮮なのですが、問題演習をしていくうちに、
これ、いつでも成り立つのでは？
という疑問が出てきます。
この疑問を次章以降で解決していきましょう。
Ⅱ n=1 でほぼ成り立つ理由
着目するのは、$~①~$の式に出てくる$~\displaystyle \sum_{k=1}^{n-1}b_k~$の部分。
数学Bの教科書や問題集で出てくる階差数列$~b_k~$の和の計算は、ほぼ全て以下の計算（実数倍やそれらの和を含めて）に帰着されます。
\begin{align*}
&\sum_{k=1}^{n-1}1=n-1 \\
\\
&\sum_{k=1}^{n-1}k=\frac{1}{2}n(n-1) \\
\\
&\sum_{k=1}^{n-1}k^2=\frac{1}{6}n(n-1)(2n-1) \\
\\
&\sum_{k=1}^{n-1}k^3=\left\{ \frac{1}{2}n(n-1) \right\}^2 \\
\\
&\sum_{k=1}^{n-1}cr^{k-1}=\frac{c(1-r^{n-1})}{1-r} ~~~(r \neq 1) \\
\end{align*} これらの式の右辺に$~n=1~$を代入してみると、見事にすべて$~0~$になります。
すなわち、数式としては変ですが、
\sum_{k=1}^{0}b_k=0~~~~\cdots ④が成り立つということです。
$④$を、$②$に代入すると、
\begin{align*}
a_1&=a_1+0 \\
a_1&=a_1
\end{align*}となり、$~\Sigma~$計算をして求まった$~\{a_n\}~$の一般項は、$~a_1~$でも必ず成り立ちます。
まとめると、 $~\displaystyle \sum_{k=1}^{0}b_k~$は定義できないものの、$~\displaystyle \sum_{k=1}^{n-1}b_k~$を計算してから$~n=1~$を代入することで、$~\displaystyle \sum_{k=1}^{0}b_k=0~$が求まるため、$~n=1~$でも成り立つということです。
Ⅲ n=1 で成り立たない例
高校範囲で出てくる階差数列を利用する問題は、ほぼ$~n=1~$でも成り立つことがわかりました。
では、$~\Sigma~$計算をして求まった$~\{a_n\}~$が、$~n=1~$で成り立たなくするにはどうすればいいのでしょう？
そのためには、$~b_k~$が、$~n=1~$と$~n \geqq 2~$で場合分けされればよいのです。
具体例を２つほど考えてみました。
$~1 , 1 , 3 , 6 , 10 , 15 , \cdots~$で与えられている数列$~\{a_n\}~$を求める。
この数列の階差数列$~\{b_n\}~$を調べると、
1 \xrightarrow{b_1=0} 1 \xrightarrow{b_2=2} 3 \xrightarrow{b_3=3} 6 \xrightarrow{b_4=4} 10 \xrightarrow{b_5=5} 15 \cdotsとなっているため、次のように表される。
b_n =
\begin{cases}
0 & (n=1) \\
n & (n \geqq 2)
\end{cases}したがって、$~n \geqq 2~$のとき、
\begin{align*}
a_n&=a_1+\sum_{k=1}^{n-1}b_k \\
\\
&=1+b_1+\sum_{k=2}^{n-1}k \\
\\
&=1+0+\left\{ \frac{1}{2}n(n-1)-1\right\} \\
\\
&=\frac{1}{2}n(n-1)~~~~\cdots ⑤
\end{align*}となる。
また、 $~n = 1~$を$⑤$に代入すると、
\begin{align*}
a_1&=\frac{1}{2}\cdot 1 \cdot (1-1) \\
\\
&=0 ~~~(\neq 1)
\end{align*}であるため、$~n=1~$のときには成り立たない。
したがって、一般項は
a_n =
\begin{cases}
1 & (n=1) \\
\\
\displaystyle \frac{1}{2}n(n-1) & (n \geqq 2)
\end{cases}と求まった。
ちょっとズルい気がしますが、確かに$~n=1~$では成り立っていません。
少し、ズルさを隠したのが次の例３です。
$~1 , 2 , 2 , 3 , 5 , 8 , \cdots~$で与えられている数列$~\{a_n\} ~$を求める。
この数列の階差数列$~\{b_n\}~$を調べると、
1 \xrightarrow{b_1=1} 2 \xrightarrow{b_2=0} 2 \xrightarrow{b_3=1} 3 \xrightarrow{b_4=2} 5 \xrightarrow{b_5=3} 8 \cdotsとなっているため、次のように表される。
b_n=|n-2|
したがって、$~n \geqq 2~$のとき、
\begin{align*}
a_n&=a_1+\sum_{k=1}^{n-1}|k-2| \\
\\
&=1+|1-2|+\sum_{k=2}^{n-1}(k-2) \\
\\
&=1+|1-2|+\left\{ \frac{1}{2}n(n-1)-2(n-1)-(1-2) \right\} \\
\\
&=1+1+\frac{1}{2}n(n-1)-2(n-1)+1 \\
\\
&=3+\frac{1}{2}(n-1)(n-4) ~~~~\cdots ⑥
\end{align*}となる。
また、 $~n = 1~$を$⑥$に代入すると、
\begin{align*}
a_1&=3+\frac{1}{2}(1-1)(1-4)
\\
&=3~~~~(\neq 1)
\end{align*}であるため、$~n=1~$のときには成り立たない。
したがって、一般項は
a_n = \begin{cases}
1 & (n=1) \\
\\
\displaystyle 3+\frac{1}{2}(n-1)(n-4) & (n \geqq 2)
\end{cases}と求まった。
絶対値を使って、$~b_n~$をスッキリ見せてはいますが、
b_n = \begin{cases}
1 & (n=1) \\
n-2 & (n \geqq 2)
\end{cases}という場合分けを含んでいるため、本質的には例２と一緒です。
おわりに
ということで、今回はよくある疑問を解消すべく、階差数列を利用した問題について解説しました。
まとめとしては以下のようになります。
階差数列型で、$n=1~$で成り立たない例は存在する！
ただ、$~n=1~$と$~n\geqq 2~$で表し方が違うような$~b_n~$でない限りは$~n=1~$でも成り立つので、ほぼ100%便宜的に $~n=1~$の確かめをしておけばOK。
ちなみにですが、$~b_n=\displaystyle \left[ \frac{1}{2}n \right]~$のように、$~n~$が奇数と偶数で場合分けされるような場合でも、$n=1~$で成り立ちます。
あくまでも、$~n=1~$と$~n\geqq 2~$ で場合分けされた$~b_n~$だけ要注意です。
な～んだ。$~n=1~$でも成り立つんだ。
うん。でも、その確かめを書き忘れると減点されちゃうから気を付けよう。
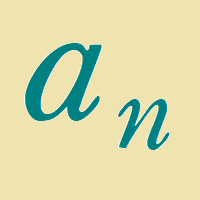
コメント
コメント一覧 （4件）
%こんなんはいかがでしょうか
数列$\{a_n\}$の階差数列$\{b_m\}$は次の式で与えられている.
\[
\textstyle\sum\limits_{k=1}^{m}b_k=\dfrac{3^m}{2}
\]
数列$\{a_n\}$の初項が$a_1=\frac{1}{2}$のとき第$n$項$a_n$を求めよ.
猫箱様
コメントありがとうございます。
確かに、一般項を求めると
$\displaystyle ~a_n=\frac{1}{2}+\frac{3^{n-1}}{2}~$
となり、$~n=1~$を代入すると、
$~a_1=1~$
で成立しませんね。
面白い例をありがとうございます。
（Texをうまく表示できなくてすみません。）
例2をいじって、bk＝｜k-3｜とかにすると、項が三つ以上存在する前提ではn=3以降で成り立つ一般項を得られます。この一般項はn=1だけでなくn=2でも成り立たなくなりますよね？
これと同様に、この例2は第２項が存在する前提で式を作ったからずれただけとは言えませんか？
数学を勉強しはじめて日が浅いので、間違っていたらすみません。
コメントありがとうございます。
\(~b_k=|k-3|~\)であれば、確かに\(~n=1~,~2~\)のときに成り立たなくなりますね。
無理やり作った数列だったので、確かにずらしただけと言うことはできますが、一応問題としては、
「\(~1 , 2 , 2 , 3 , 5 , 8 , \cdots~\)で与えられている数列\( ~\{a_n\} ~\)を求める。」
としているので、第２項である\(~a_2=2~\)が存在しているという仮定のもとで考えています。
もし、問題文が
「初項\(~1~\)である数列\( ~\{a_n\}~\)の階差数列\( ~\{b_n\}~\)が、\(~b_n=|n-2|~\)と与えられたとき、\(~a_n~\)の一般項を求めなさい」
とかであれば、議論の余地があるのかもしれませんが・・・。
お答えになっているでしょうか？