三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。
この記事では、「モナ・リザ」や「最後の晩餐」で有名な芸術家レオナルド・ダ・ヴィンチが考案した証明方法を、現役数学教員がわかりやすく解説します。
ユークリッドと同様の図に補助線を加え、六角形の面積に着目するという一風変わった証明。
色付きの図で解説しているので、この記事を読むことで、その芸術的な解法を理解できます。
- ダ・ヴィンチと数学の関わり
- レオナルド・ダ・ヴィンチが考えた三平方の定理の証明方法
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓

レオナルド・ダ・ヴィンチと数学
レオナルド・ダ・ヴィンチと黄金比
芸術家として名を残しているレオナルド・ダ・ヴィンチ(Leonardo da Vinci , 1452-1519)ですが、彼は数学の才も併せ持っていました。

(出典;Leonardo da Vinci, Public domain, via Wikimedia Commons)
彼の代表作である「モナ・リザ」では、顏の縦横比が黄金比となっていることで有名です。
絵画の中に数学を混ぜることで、論理的に美を表現しました。

(出典:Leonardo da Vinci, Public domain, via Wikimedia Commons より改変)
レオナルド・ダ・ヴィンチに数学的な影響を与えた人物
ダ・ヴィンチに関する数学的著作は無いものの、その時代のイタリアの数学者ルカ・パチョーリ(Luca Pacioli , 1445-1517)との交友関係が、ダ・ヴィンチに数学的な影響を与えたとされています。

(出典:Attributed to Jacopo de’ Barbari, Public domain, via Wikimedia Commons)
ルカ・パチョーリの著書『神聖な比例について』では、ダ・ヴィンチが友人のために斜方立方八面体を描くほどの仲でした。
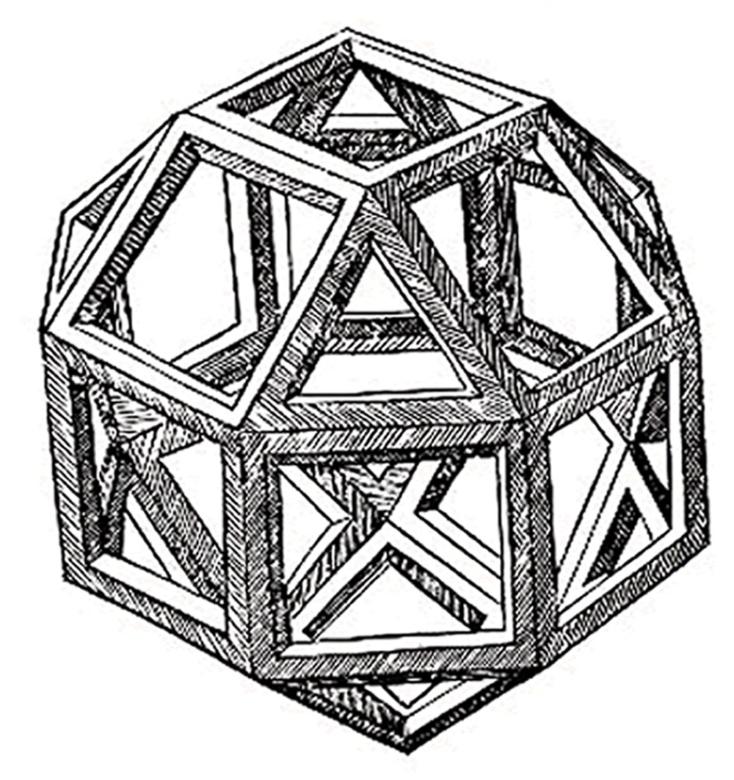
(出典: Public domain, via Wikimedia Commons )
ルカ・パチョーリは、ユークリッドの『原論』に関する講義や出版もしており、ダ・ヴィンチにとっても『原論』は身近な数学書となっていたと考えられています。
その『原論』には、ユークリッドによる三平方の定理の証明方法が載っていたため、そこから着想を得てダ・ヴィンチオリジナルの証明にまで至ったと思われます。

レオナルド・ダ・ヴィンチの証明
ダ・ヴィンチにとって、ユークリッドの『原論』は身近であったため、証明の出発点ともなる図は同じものです。
そこからさらに補助線を加えてできる六角形を考えていくため、図をよく見ながら証明を読み進めてください。
$~\angle A=90^{\circ}~$の直角三角形$~ABC~$において、各辺を1辺とする正方形を$~\triangle ABC~$の外側にそれぞれ図5のように作る。
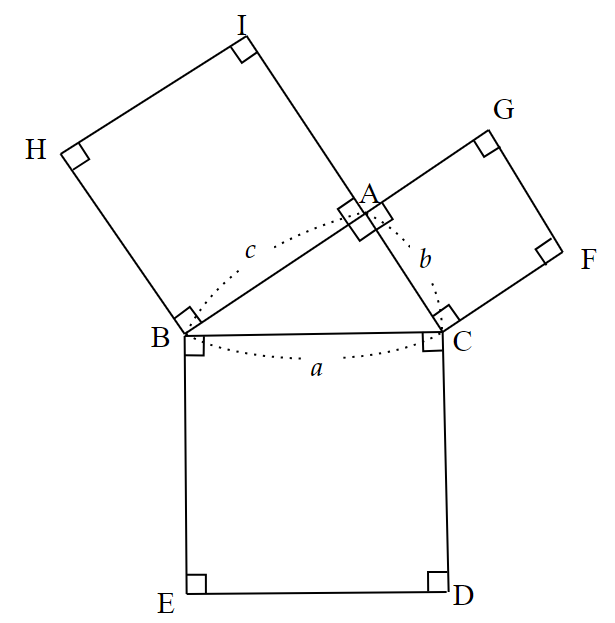
ここで、$~I~$と$~G~$を結び、さらに$~\triangle ABC~$と合同な三角形$~JDE~$を図6のように作る。
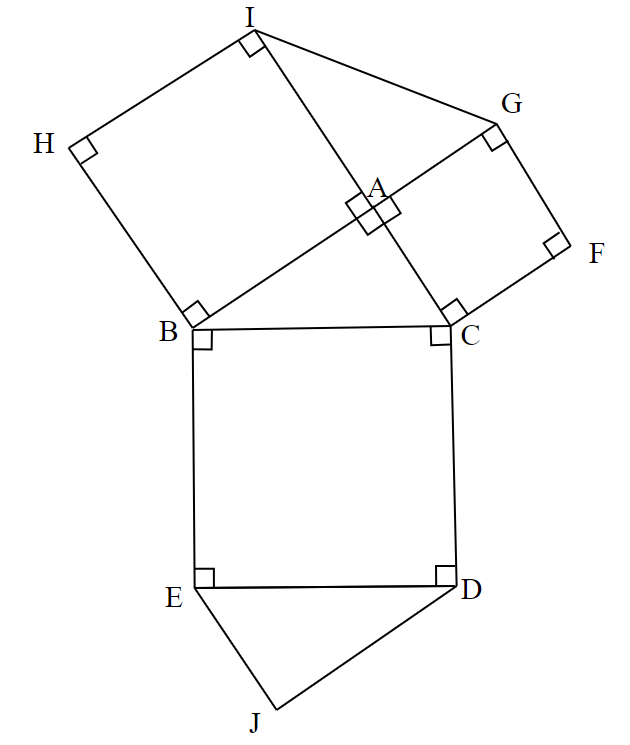
図2において、等しい辺の長さ、等しい角の大きさをそれぞれ色で分けると、図7のようになる。
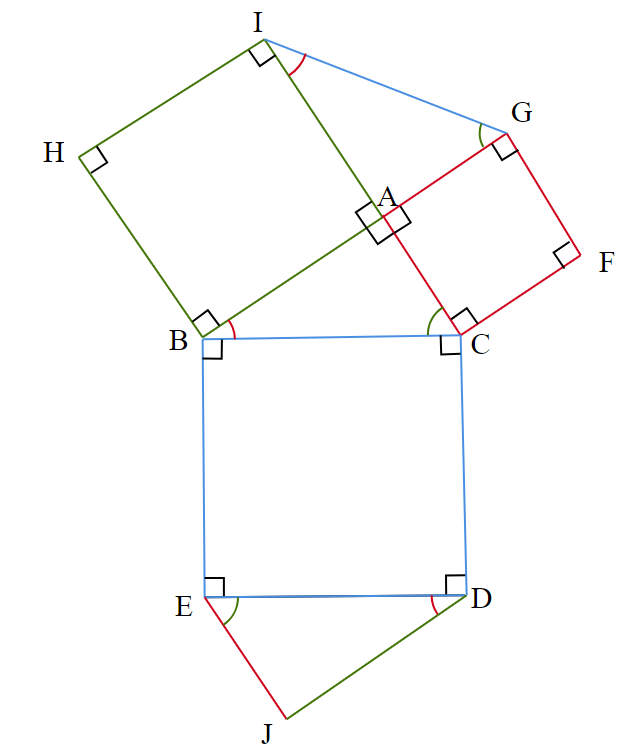
図7より、$~\triangle ABC~\equiv~\triangle AIG~$が言える。
次に、四角形ABEJ、四角形JDCA、四角形HBCF、四角形HIGFに注目すると、
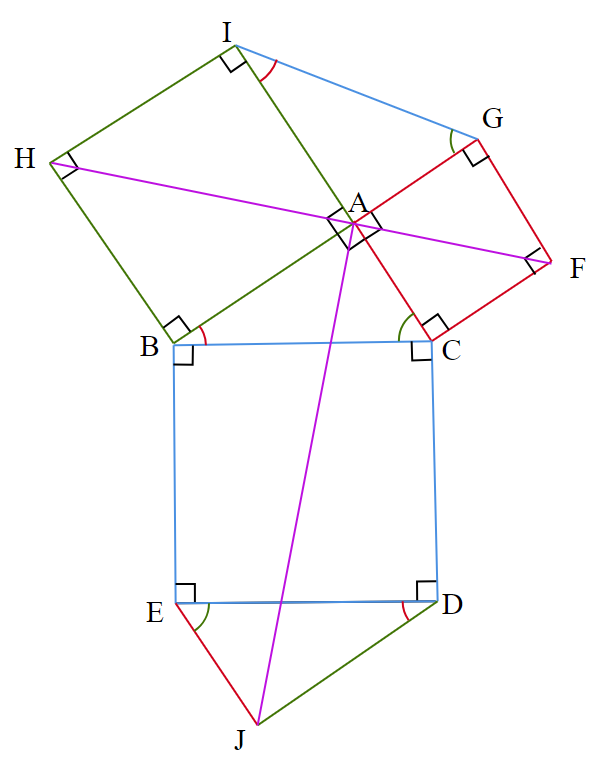
図8において、
- $~AB=JD=HB=HI~$
- $~∠ABE=∠JDC=∠HBC=∠HIG=90^{\circ}+∠B~$
- $~BE=DC=BC=IG~$
- $~∠BEJ=∠DCA=∠BCF=∠IGF=90^{\circ}+∠C~$
- $~EJ=CA=CF=GF~$
であるため、
四角形$~ABEJ~$$\equiv~$四角形$~JDCA ~$$\equiv~$四角形$~HBCF~$$\equiv~$四角形$~HIGF$
となる。
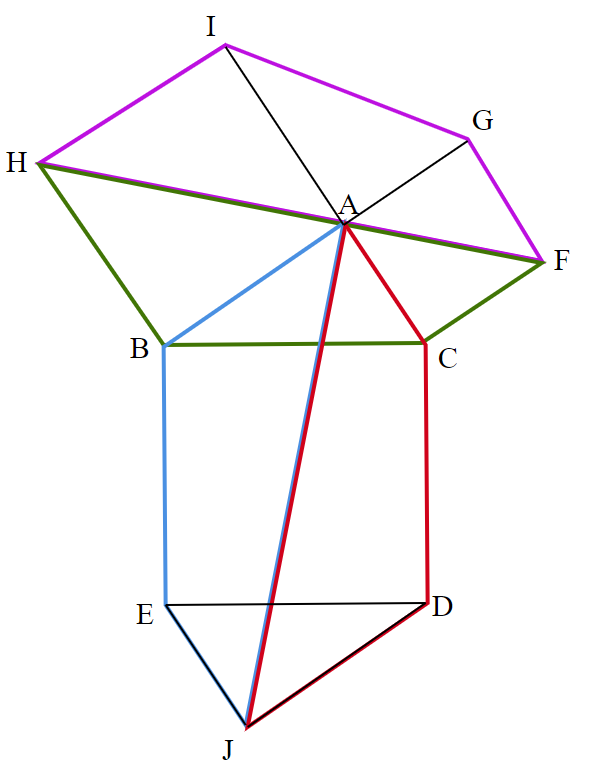
図10のように、合同な四角形を2つ組み合わせてできる六角形$~ABEJDC~$と六角形$~HBCFGI~$について考える。
共通している$~\triangle ABC~$と合同な三角形$~\triangle JED~$と $~\triangle AGI~$を引くことで、
正方形BCDE=正方形ACFG+正方形ABHI
がわかる。
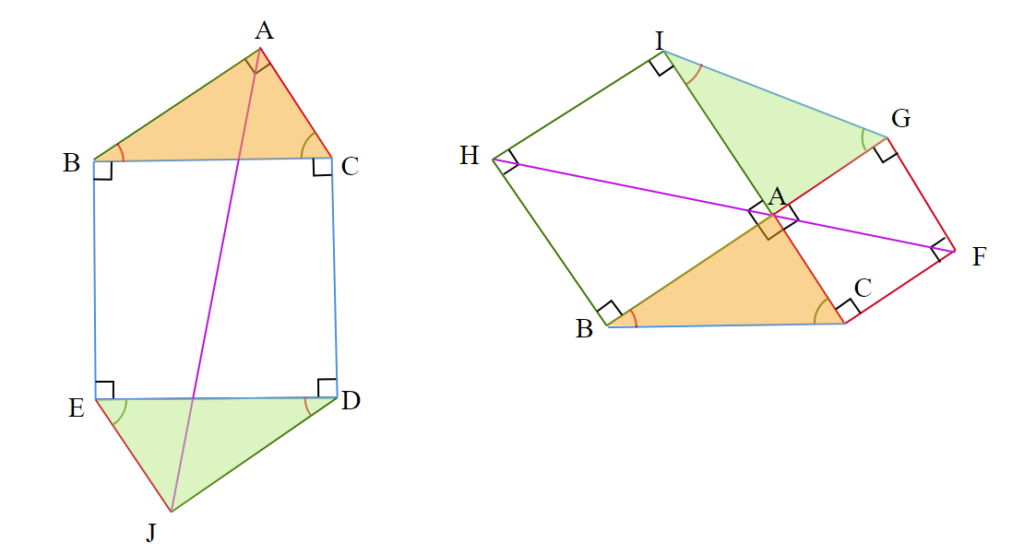
したがって、$~c^2=a^2+b^2~$が示された。■
合同な四角形から、六角形の面積が等しいことを言い、被っている三角形を引いていくと、正方形だけが残るという戦法でした。

さすが、芸術家。図形を絵として捉えていたのかな?



うん。補助線を引いてできた六角形に注目するなんて、普通はできないよね。
・平野 葉一(2019)「レオナルド・ダ・ヴィンチの数学研究 ― 知と技の間で」<http://www.mathsoc.jp/publication/tushin/2402/2402hirano.pdf>2022.1.3アクセス.
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓



コメント