私学適性（数学）令和3年度解説　大問２

他の年度については、コチラからどうぞ。

　サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
　解説の内容自体に影響はありません。

---

問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。

---

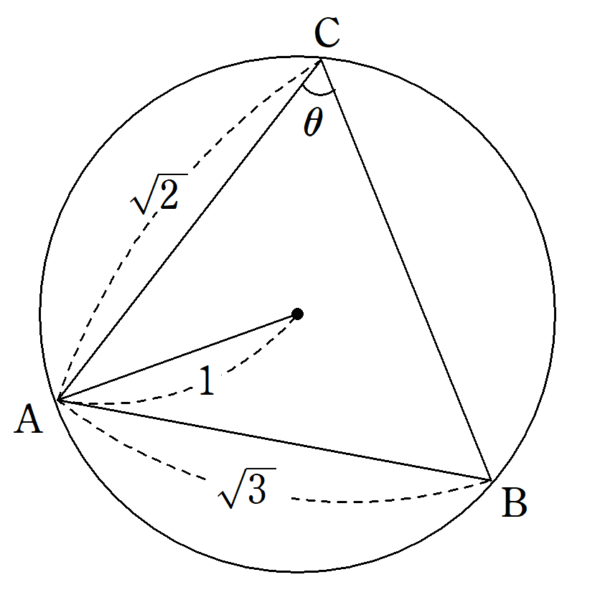
１(1)

①　正弦定理より、
\begin{align}
2 \cdot 1 &=\frac{\sqrt{3}}{\sin{\theta}} \\
\\
2\sin{\theta}&=\sqrt{3} \\
\\
\sin{\theta}&=\frac{\sqrt{3}}{2}
\end{align}
と求まる。
 
②　①より、$~\theta=60^{\circ}~$なので、余弦定理より、
\begin{align}
(\sqrt{3})^2&=(\sqrt{2})^2+BC^2-2\cdot \sqrt{2} \cdot BC \cdot \cos{60^{\circ}} \\
\\
3&=2+BC^2-2\cdot \sqrt{2} \cdot BC \cdot \frac{1}{2} \\
\\
0&=BC^2-\sqrt{2}BC-1 \\
\end{align}
が成り立ち、ここで解の公式を使うことで、
\begin{align}
BC&=\frac{-(-\sqrt{2})\pm \sqrt{(-\sqrt{2})^2-4\cdot 1 \cdot (-1)}}{2 \cdot 1} \\
\\
&=\frac{\sqrt{2} \pm \sqrt{6}}{2}
\end{align}
であり、$~BC > 0~$より、$~BC=\displaystyle \frac{\sqrt{2} + \sqrt{6}}{2}~$と求まる。
 
③　面積の公式を使うと、
\begin{align}
\triangle ABC&=\frac{1}{2} \cdot CA \cdot CB \cdot \sin{\theta} \\
\\
&= \frac{1}{2} \cdot \sqrt{2} \cdot \frac{\sqrt{2} + \sqrt{6}}{2} \cdot \frac{\sqrt{3}}{2} \\
\\
&=\frac{\sqrt{6}}{8} (\sqrt{2} + \sqrt{6}) \\
\\
&=\frac{2\sqrt{3}+6}{8} \\
\\
&=\frac{\sqrt{3}+3}{4}
\end{align}
が求まる。

---

１(2)
与式の$~y~,~z~$の項を括ると、
\begin{equation}
6x+5(3y+7z)=4
\end{equation}
であり、$~3y+7z=a~$とすると、
\begin{equation}
6x+5a=4~~~\cdots ①
\end{equation}
で、特殊解の$~x=-1~,~a=2~$から、
\begin{equation}
6\cdot (-1)+5\cdot 2 =4~~~\cdots ②
\end{equation}
が成り立つ。
 
$①-②~$より、
\begin{align}
6(x+1)+5(a-2) &=0 \\
6(x+1)&=-5(a-2)
\end{align}
で、$~6~$と$~5~$は互いに素であることから、
\begin{align}
x+1=-5k~&,~a-2=6k~~~(~k~は整数) \\
x=-5k-1~&,~a=6k+2
\end{align}
が求まる。
 
次に、$~y~,~z~$を求める。
\begin{equation}
3y+7z=6k+2~~~\cdots ③
\end{equation}
で、特殊解の$~y=2k+3~,~z=-1~$から、
\begin{equation}
3\cdot (2k+3)+7\cdot (-1) =6k+2~~~\cdots ④
\end{equation}
が成り立つ。（$~k~$と定数の恒等式として特殊解を出す）
 
$③-④~$より、
\begin{align}
3(y-2k-3)+7(z+1) &=0 \\
3(y-2k-3)&=-7(z+1)
\end{align}
で、$~3~$と$~7~$は互いに素であることから、
\begin{align}
y-2k-3=-7 \ell ~&,~z+1=3 \ell ~~~(~\ell~は整数) \\
y=2k-7\ell+3~&,~z=3 \ell -1
\end{align}
が求まった。

---

１(3)
$~f(x)~$を変形していく。
$~\sin^2{x}=1-\cos^2{x}~$より、

\begin{align}
f(x)&=a\cos^2{x}+\sqrt{3}(a-b)\cos{x}\sin{x}+b(1-\cos^2{x}) \\
&=(a-b)\cos^2{x}+\sqrt{3}(a-b)\cos{x}\sin{x}+b \\
&=(a-b)(\cos^2{x}+\sqrt{3}\cos{x}\sin{x})+b
\end{align}

\begin{align}
&~~~f(x) \\
&=a\cos^2{x}+\sqrt{3}(a-b)\cos{x}\sin{x} \\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+b(1-\cos^2{x}) \\
&=(a-b)\cos^2{x}+\sqrt{3}(a-b)\cos{x}\sin{x}+b \\
&=(a-b)(\cos^2{x}+\sqrt{3}\cos{x}\sin{x})+b
\end{align}

であり、２倍角の公式を変形した$~\displaystyle \cos^2{x}=\frac{\cos{2x}+1}{2}~$、$~\displaystyle \cos{x}\sin{x}=\frac{1}{2}\sin{2x}~$をそれぞれ代入し、

\begin{align}
f(x)&=(a-b)\left( \frac{\cos{2x}+1}{2}+\frac{\sqrt{3}}{2}\sin{2x} \right)+b \\
\\
&=(a-b)\left( \frac{\cos{2x}}{2}+\frac{\sqrt{3}}{2}\sin{2x}+\frac{1}{2} \right)+b \\
\\
&=(a-b)\left( \frac{1}{2} \cdot \cos{2x}+\frac{\sqrt{3}}{2} \cdot \sin{2x}+\frac{1}{2} \right)+b \\
\end{align}

\begin{align}
&~~~f(x) \\
\\
&=(a-b)\left( \frac{\cos{2x}+1}{2}+\frac{\sqrt{3}}{2}\sin{2x} \right)+b \\
\\
&=(a-b)\left( \frac{\cos{2x}}{2}+\frac{\sqrt{3}}{2}\sin{2x}+\frac{1}{2} \right)+b \\
\\
&=(a-b)\left( \frac{1}{2} \cdot \cos{2x}+\frac{\sqrt{3}}{2} \cdot \sin{2x}+\frac{1}{2} \right)+b \\
\end{align}

となる。
ここで、加法定理を使うことで、
\begin{equation}
f(x)=(a-b)\left\{ \cos{\left( \frac{\pi}{3}-2x \right) }+\frac{1}{2} \right\}+b
\end{equation}
であるため、$~f(x)~$が最大値$~5~$をとるのは$~\displaystyle \cos{\left( \frac{\pi}{3}-2x \right) }=1~$のときで、
\begin{align}
(a-b)\left( 1+\frac{1}{2} \right)+b&=5 \\
\\
\frac{3}{2}a-\frac{3}{2}b+b&=5 \\
\\
3a-b&=10 ~~~\cdots ①
\end{align}
が成り立つ。
また、$~f(x)~$が最小値$~3~$をとるのは$~\displaystyle \cos{\left( \frac{\pi}{3}-2x \right) }=-1~$のときで、
\begin{align}
(a-b)\left( -1+\frac{1}{2} \right)+b&=3 \\
\\
-\frac{1}{2}a+\frac{1}{2}b+b&=3 \\
\\
-a+3b&=6 ~~~\cdots ②
\end{align}
が成り立つため、$~①~,~②~$を連立することで、
\begin{equation}
a=\frac{9}{2}~,~b=\frac{7}{2}
\end{equation}
が求まる。

---

１(4)
①
\begin{equation}
(与式)=2\log_3{x}+( \log_3{x} )^2
\end{equation}
で、$~\displaystyle \log_3{x}=t~$とすると、
\begin{equation}
2t+t^2=(t+1)^2-1
\end{equation}
であり、$~t=-1~$のとき、最小値$~-1~$をとるので、
\begin{align}
\log_3{x}&=-1 \\
x&=3^{-1} \\
x&=\frac{1}{3}
\end{align}
と求まる。
 
②
\begin{equation}
(与式)=\log_3{xy} ~~~\cdots ①
\end{equation}
より、$~xy~$の最大値を求めればよい。
$~x=18-3y~$を代入することで、
\begin{align}
xy&=(18-3y)y \\
&=-3y^2+18y \\
&=-3(y-3)^2+27 \\
\end{align}
であり、$~\log_3{x}~,~\log_3{y}~$より、$~y~$の変域は、
\begin{align}
18-3y > 0 ~&,~ y > 0 \\
y < 6 ~&,~ y > 0 \\
0 < &y < 6
\end{align}
なので、$~y=3~$のときに$~xy~$は最大値$~27~$をとる。
よって、$~①~$に代入して、
\begin{equation}
\log_3{27}=\log_3{3^3}=3
\end{equation}
と求まった。

---

１(5)
$~n~$群の最後の項の、全体の数列における順番を$~a_n~$項目とすると、
\begin{equation}
a_1=1~,~a_2=3~,~a_3=6~,~a_4=10~,~a_5=15
\end{equation}
という階差数列となっているため、
\begin{align}
a_n&=a_1+\sum_{k=1}^{n-1} (k+1) \\
\\
&=1+\frac{1}{2}n(n-1)+(n-1) \\
\\
&=\frac{1}{2}n^2+\frac{1}{2}n \\
\\
&=\frac{1}{2}n(n+1)
\end{align}
が求まり、$~\displaystyle a_1=\frac{1}{2} \cdot 1 \cdot 2=1~$も成り立っている。
 
ここで、$~2020~$項目における自然数を$~n~$とすると、次のような関係になる。

すなわち、
\begin{align}
a_{n-1} &< 2020 \le a_{n} \\
\end{align}
を満たす$~n~$を求めればよい。
 
不等式を解くよりも、ある程度見当をつけて$~n~$の値を代入したほうが速い。
\begin{align}
a_{60}&=\frac{1}{2}\cdot 60 \cdot 61=1830 \\
\\
a_{61}&=\frac{1}{2}\cdot 61 \cdot 62=1891 \\
\\
a_{62}&=\frac{1}{2}\cdot 62 \cdot 63=1953 \\
\\
a_{63}&=\frac{1}{2}\cdot 63 \cdot 64=2016 \\
\\
a_{64}&=\frac{1}{2}\cdot 64 \cdot 65=2080
\end{align}
よって、求めたい自然数は$~64~$となる。

---

１(6)
\begin{align}
\vec{a}+t\vec{b}&=(~1+2t~,~8+t~) \\
\end{align}
より、$~|\vec{a}+t\vec{b}|=15~$の両辺を２乗して、
\begin{align}
1+4t+4t^2+64+16t+t^2&=225 \\
5t^2+20t-160&=0 \\
t^2-4t-32&=0 \\
(t-4)(t+8)&=0 \\
t&=4~,~-8
\end{align}
と求まる。
 
ここで、
\begin{equation}
\vec{a}-2t\vec{b}=(~1-4t~,~8-2t~)
\end{equation}
であり、$~t=4~$を代入すると、
\begin{equation}
\vec{a}-2t\vec{b}=(~-15~,~0~)
\end{equation}
なので、$~|\vec{a}-2t\vec{b}|=15~$となる。
 
同様に、$~t=-8~$を代入すると、
\begin{equation}
\vec{a}-2t\vec{b}=(~33~,~24~)
\end{equation}
なので、$~|\vec{a}-2t\vec{b}|\neq 15~$で不適。
 
以上より、$~t=4~$のみとなり、求めたいベクトルは
\begin{equation}
\vec{a}+4\vec{b}=(~9~,~12~)
\end{equation}
となる。

---

１(7)
\begin{equation}
\int_{x}^{a}f(t)~dt=-\int_{a}^{x}f(t)~dt
\end{equation}
であるため、与式に代入すると、
\begin{align}
-\int_{a}^{x}f(t)~dt&=2x^2-5x+2 \\
\\
\int_{a}^{x}f(t)~dt&=-2x^2+5x-2 ~~~\cdots ① \\
\end{align}
となり、両辺$~x~$で微分することで、
\begin{equation}
f(x)=-4x+5
\end{equation}
と求まる。
 
これを、$①$に代入することで、
\begin{align}
\int_{a}^{x}-4t+5 ~dt&=-2x^2+5x-2 \\
\\
\left[ -2t^2+5t \right]_{a}^{x}&=-2x^2+5x-2 \\
\\
-2x^2+5x+2a^2-5a&=-2x^2+5x-2 \\
2a^2-5a+2&=0 \\
(a-2)(2a-1)&=0 \\
a&=2~,~\frac{1}{2}
\end{align}
と求まった。

---

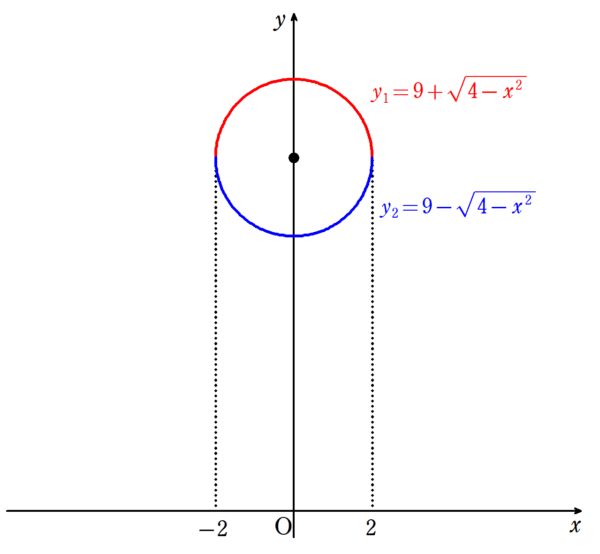
１(8)
この円における$~x~$の変域は$~-2 \le x \le 2~$より、$~4-x^2 \ge 0~$なので、
\begin{align}
x^2+(y-9)^2&=4 \\
(y-9)^2&=4-x^2 \\
y-9&=\pm \sqrt{4-x^2} \\
y&=9 \pm \sqrt{4-x^2} \\
\end{align}
と変形でき、$~y_1~,~y_2~$を
\begin{equation}
y_1=9 + \sqrt{4-x^2}~,~y_2=9 – \sqrt{4-x^2}
\end{equation}
と定義する。

この円を$~x~$軸のまわりに１回転させてできる回転体の体積は、
\begin{align}
&~~~\int_{-2}^{2}y_{1}^2~dx-\int_{-2}^{2}y_{2}^2~dx \\
\\
&=2\pi \int_{0}^{2}y_{1}^2-y_{2}^2~dx \\
\\
&=2\pi \int_{0}^{2}(y_1+y_2)(y_1-y_2)~dx \\
\\
&=2\pi \int_{0}^{2}18 \cdot 2\sqrt{4-x^2}~dx \\
\\
&=72\pi \int_{0}^{2} \sqrt{4-x^2}~dx \\
\end{align}
であり、ここで$~x=2\sin{\theta}~$と置換することで、$~\displaystyle \theta:0 \to \frac{\pi}{2}~$、$~\displaystyle \frac{dx}{d\theta}=2\cos{\theta}~$より、
\begin{align}
&=72\pi \int_{0}^{\frac{\pi}{2}} \sqrt{4-4\sin^2{\theta}}\cdot 2\cos{\theta}~d\theta \\
\\
&=72\pi \int_{0}^{\frac{\pi}{2}} 2\cos{\theta} \cdot 2\cos{\theta}~d\theta \\
\\
&=288 \pi \int_{0}^{\frac{\pi}{2}} \cos^2{\theta}~d\theta \\
\end{align}
となり、２倍角の公式$~\displaystyle \cos{2\theta}=2\cos^2{\theta}-1~$を利用して、
\begin{align}
&=288 \pi \int_{0}^{\frac{\pi}{2}} \frac{\cos{2\theta}+1}{2}~d\theta \\
\\
&=144 \pi \int_{0}^{\frac{\pi}{2}} \cos{2\theta}+1~d\theta \\
\\
&=144 \pi \left[ \frac{\sin{2\theta}}{2}+\theta \right]_{0}^{\frac{\pi}{2}} \\
\\
&=144 \pi \cdot \frac{\pi}{2} \\
\\
&=72 \pi^2
\end{align}
と求まった。

---

---

◇参考文献等
・『私学教員適性検査問題集　数学（令和元年度～令和3年度）』