東京都私学教員適性検査の過去問(令和3年度)の答えを解説付きで載せています。
問題集の解答例で、解法を調べたい際にご活用ください。
大問1(本ページ)
大問2
※大問3~5に関しては、問題集の解答の中に解法まで載っています。
他の年度については、コチラからどうぞ。
サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
解説の内容自体に影響はありません。
問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。
1
(1) $~(3x+2y-1)(2x-y+4)~$
(2) $~-\displaystyle \frac{\sqrt{3}}{3} < x \le \frac{12}{5}~$
(3) $~252~$個
(4) $~\displaystyle \frac{42}{107}~$
(5) $~33~$桁
(6) $~x~$
(7) $~14~$
(8) $~\displaystyle a_n=\frac{1}{2}(3^n-1)~$
(9) $~\displaystyle \frac{1}{2}~$
(10) $~\displaystyle \frac{x^2}{9}+\frac{y^2}{16}=1~$
(11) $~\displaystyle y=\pm \frac{2}{3}(x-1)~$
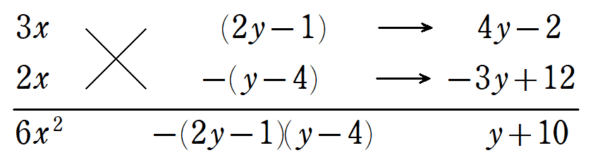
1(1)
まずは与式を降べきの順にする。
\begin{align}
&~~~(与式) \\
&=6x^2+(10+y)x-(2y^2-9y+4) \\
&=6x^2+(10+y)x-(2y-1)(y-4) \\
\end{align}
ここで、式のたすきがけを行うと、
となるので、
\begin{align}
&~~~\left\{ 3x+(2y-1) \right\} \left\{ 2x-(y-4) \right\} \\
&=(3x+2y-1)(2x-y+4)
\end{align}
と求まる。
1(2)
1本目の二次不等式を解く。$~3x^2-5\sqrt{3}x-6=0~$の解は、
\begin{align}
x&=\frac{5\sqrt{3}\pm \sqrt{75+72}}{6} \\
\\
&=\frac{5\sqrt{3} \pm 7\sqrt{3}}{6} \\
\\
&=2\sqrt{3}~,~-\frac{1}{3}\sqrt{3}
\end{align}
となるため、不等式の解は、
\begin{equation}
-\frac{1}{3}\sqrt{3} < x < 2\sqrt{3} ~~~\cdots ①
\end{equation}
となる。
2本目の一次不等式を解く。両辺を$~6~$倍して、
\begin{align}
4x+6 &\ge 9x-6 \\
-5x &\ge -12 \\
x \le \frac{12}{5} ~~~\cdots ②
\end{align}
となる。
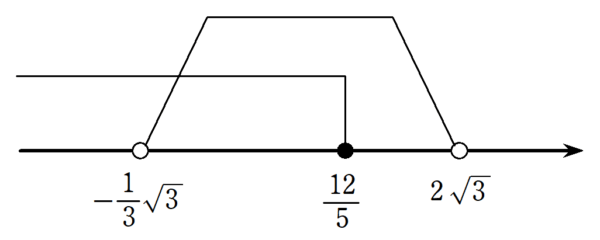
$①$と$②$より、
解の共通範囲を考えると、$~\displaystyle -\frac{1}{3}\sqrt{3} < x \le \frac{12}{5}~$が求まる。
1(3)
(ⅰ) $~1~$から$~99~$までの整数で、0を2個含むものは存在しない。
(ⅱ) $~100~$から$~999~$までの整数の場合、
千の位は1から9の$~9~$通り。
十の位と一の位が0ならば条件を満たすので、
\begin{equation}
9 \times 1 \times 1=9 個
\end{equation}
となる。
(ⅲ) $~1000~$から$~9999~$までの整数の場合、
千の位は1から9の$~9~$通り。
百の位、十の位、一の位の中の2つが0で、残りの位は1から9の$~9~$通りなので、
\begin{equation}
9 \times _3C_2 \times 9=243 個
\end{equation}
となる。
(ⅰ)~(ⅲ)より、$~9+243=252~$個が0を2個含む整数となる。
1(4)
A、B、Cから赤玉が取り出される確率は、それぞれ$ \displaystyle ~\frac{3}{5}~,~\frac{1}{2}~,~\frac{3}{7}~$。
また、A、B、Cの袋が選ばれる確率はそれぞれ$~\displaystyle \frac{1}{3}~$ずつである。
よって、無作為に箱を1つ選び、玉を1個取り出したときに赤玉となる確率は、
\begin{align}
&~~~~\frac{1}{3}\cdot \frac{3}{5}+\frac{1}{3}\cdot \frac{1}{2}+\frac{1}{3}\cdot \frac{3}{7} \\
\\
&=\frac{1}{5}+\frac{1}{6}+\frac{1}{7} \\
\\
&=\frac{107}{210}
\end{align}
となる。
よって、選んだ箱がAとなる条件付き確率は、
\begin{equation}
\frac{\frac{1}{3}\cdot \frac{3}{5}}{\frac{107}{210}}=\frac{42}{107}
\end{equation}
と求まる。
1(5)
$~\displaystyle \log_2{5\cdot 8^{10}}~$の整数部分を求める。
\begin{align}
\log_2{5\cdot 8^{10}}&=\log_2{5}+\log_2{8^{10}} \\
&=\log_2{5}+10\log_2{2^3} \\
&=\log_2{5}+30\log_2{2} \\
&=\log_2{5}+30 \\
\end{align}
であるため、$~2=\log_2{4} < \log_2{5} < \log_2{8}=3~$より、
\begin{equation}
32 < \log_2{5\cdot 8^{10}} < 33
\end{equation}
とわかる。
よって、$~5\cdot 8^{10}~$を2進法で表すと、33桁である。
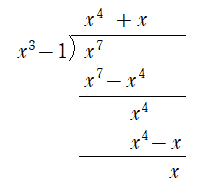
1(6)
下のように筆算をすることで、余りは$~x~$とわかる。
1(7)
\begin{align}
f(1)&=3\cdot 1-1=2 \\
f(4)&=3 \cdot 4^2-4=44
\end{align}
より、平均変化率は
\begin{align}
\frac{f(4)-f(1)}{4-1}&=\frac{44-2}{3} \\
&=14
\end{align}
と求まる。
1(8)
$~\displaystyle a_{n+1}=a_n+3^n~$の両辺を$~3^{n+1}~$で割ると、
\begin{align}
\frac{a_{n+1}}{3^{n+1}}&=\frac{a_{n}}{3^{n+1}}+\frac{3^n}{3^{n+1}} \\
\\
\frac{a_{n+1}}{3^{n+1}}&=\frac{1}{3} \cdot \frac{a_{n}}{3^{n}}+\frac{1}{3} \\
\end{align}
となる。ここで、$~\displaystyle b_n=\frac{a_n}{3^n}~$とすると、
\begin{align}
b_{n+1}&=\frac{1}{3}b_n+\frac{1}{3} \\
\\
b_{n+1}-\frac{1}{2}&=\frac{1}{3} \left( b_n-\frac{1}{2} \right) \\
\\
b_n-\frac{1}{2}&=\left( \frac{1}{3} \right)^{n-1} \cdot \left( b_1-\frac{1}{2} \right) \\
\end{align}
となるので、$~\displaystyle b_1=\frac{a_1}{3^1}=\frac{1}{3}~$より、
\begin{align}
b_{n}&=\left( \frac{1}{3} \right)^{n-1} \cdot \left( \frac{1}{3}-\frac{1}{2} \right)+\frac{1}{2} \\
\\
&=-\frac{1}{6} \left( \frac{1}{3} \right)^{n-1} +\frac{1}{2} \\
\\
&=-\frac{1}{2} \left( \frac{1}{3} \right)^{n} +\frac{1}{2} \\
\end{align}
が求まる。
$~b_n~$を戻すことで、
\begin{align}
\frac{a_n}{3^n}&=-\frac{1}{2} \left( \frac{1}{3} \right)^n+\frac{1}{2} \\
\\
a_n&=-\frac{1}{2}+\frac{3^n}{2} \\
\\
a_n&=\frac{1}{2} \left( 3^n-1 \right)
\end{align}
と求まる。
1(9)
\begin{align}
&~~~(与式) \\
\\
&=\lim_{x \to \infty}\frac{\left(\sqrt{x^2+x}-x \right)\left(\sqrt{x^2+x}+x \right)}{\left(\sqrt{x^2+x}+x \right)} \\
\\
&=\lim_{x \to \infty}\frac{\left(\sqrt{x^2+x} \right)^2-x^2}{\sqrt{x^2+x}+x} \\
\\
&=\lim_{x \to \infty}\frac{x^2+x-x^2}{\sqrt{x^2+x}+x } \\
\\
&=\lim_{x \to \infty}\frac{x}{\sqrt{x^2+x}+x } \\
\\
&=\lim_{x \to \infty}\frac{1}{\sqrt{1+\frac{1}{x}}+1 } \\
\\
&=\frac{1}{\sqrt{1}+1} \\
\\
&=\frac{1}{2}
\end{align}
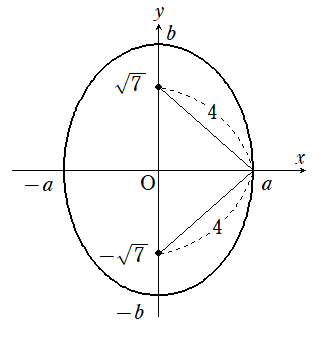
1(10)
焦点からの距離の和が一定なので、楕円とわかる。
求めたい楕円の方程式を
\begin{equation}
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ~~~( a < b )
\end{equation}
とすると、焦点からの距離の和が$~8~$であることから、次のような図が書ける。
図より、$~b=4~$となり、三平方の定理から、
\begin{align}
(\sqrt{7})^2+a^2&=4^2 \\
a^2&=9 \\
a&=3
\end{align}
なので、求めたい図形の方程式は
\begin{equation}
\frac{x^2}{9}+\frac{y^2}{16}=1
\end{equation}
と求まる。
1(11)
双曲線$~\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1~$の漸近線は$~\displaystyle y=\pm \frac{b}{a}x~$で与えられるので、
\begin{equation}
y=\pm \frac{2}{3}(x-1)
\end{equation}
と求まる。
(6)や(7)の難易度の低さにビックリ!
また、(10),(11)も二次曲線の知識があれば簡単です。
昔のような、計算力を試すような問題が減ってきた気がします。

◇参考文献等
・『私学教員適性検査問題集 数学(令和元年度~令和3年度)』
コメント