テイラーの定理～具体例からわかりやすく解説！　剰余項の由来はコーシーの平均値の定理！？～

　解析学で非常に重要な「テイラー級数」。その基になっているのが「テイラーの定理」です。
　剰余項を含め、定理の内容を具体例からわかりやすく解説し、証明へと進みます。

Ⅰ　テイラーの定理とは？

Ⅰー①　テイラーの定理の内容

　テイラーの定理はテイラーの公式とも呼ばれ、以下のような内容となっています。

\begin{align*}
f(x)&=f(a)+(x-a)\frac{f'(a)}{1!}+(x-a)^2\frac{f^{\prime\prime}(a)}{2!}+\cdots  \\
&~~~~~~~~~~~~~~~~+(x-a)^{n-1}\frac{f^{(n-1)}(a)}{(n-1)!}+(x-a)^n\frac{f^{(n)}(\xi)}{n!}
\end{align*}

　$~\xi~$は「クシー」と読み、この$~\xi~$の条件に関しては、$~a \lessgtr \xi \lessgtr x~$や$~\xi=a+\theta(x-a)~~(0 < \theta < 1)~$と表されることもあります。

　また、右辺の最後の項だけ$~\xi~$を使っており、この最終項のことを

R_n=(x-a)^n \frac{f^{(n)}(\xi)}{n!}

と表し、剰余項といいます。

　この定理について解説する前に、発見者についても触れておきましょう。

Ⅰー②　テイラーの定理の発見者

　テイラーの定理は、イギリスの数学者ブルック・テイラー（Brook Taylor , 1685-1731）によって発見されました。
　彼が1715年に書いた『増分法』の中に、テイラーの定理が載っています。

　しかし、現在の解析学において重要なマクローリン展開の基礎となるテイラーの定理も、当時は重要視されていませんでした。

　また、テイラーは剰余項について考えていなかったため、公式としてはアバウトなものでした。

　この公式が日の目を浴びるのは、18世紀後半。
　1772年にテイラーの定理が「微分法の基礎となる原理」として認められ、ジョゼフ・ルイ・ラグランジュ（Joseph-Louis Lagrange , 1736-1813）が剰余項について言及しました。

　これにより、テイラーの定理が現在の形になり、ラグランジュの功績も讃えて、$~R_n~$をラグランジュの剰余ともいいます。

Ⅱ　テイラーの定理の意味

　テイラーの定理の意味を一言で表すと、

どんな関数も、ある点の周りに限定すれば多項式で近似できる

となります。

Ⅱー①　３次関数を１次関数で近似する

　手始めに次の例題を考えてみます。

　接線というのは直線、すなわち一次式です。
　数学Ⅱの知識でこの例題は解くことができます。

f'(x)=3x^2-6x-6

\begin{align*}
f'(3)&=3\cdot 3^2-6\cdot 3-6 \\
&=27-18-6 \\
&=3
\end{align*}

\begin{align*}
f(3)&=3^3-3\cdot 3^2-6 \cdot 3+8 \\
&=27-27-18+8 \\
&=-10
\end{align*}

\begin{align*}
y-f(3)&=f'(3)(x-3) \\
y&=f(3)+(x-3)f'(3) ~~~~\cdots ① \\
y&=-10+(x-3)\cdot 3 \\
y&=3x-19
\end{align*}

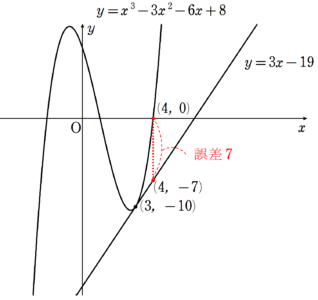
　さて、もとの三次関数と、求まった接線をグラフに表すと、図３のようになります。

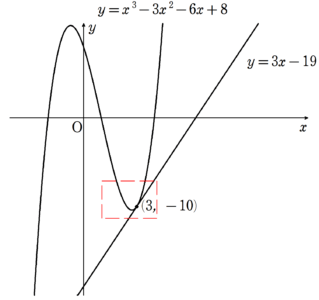
　図３の赤枠内を拡大すると、以下の図４のようになります。

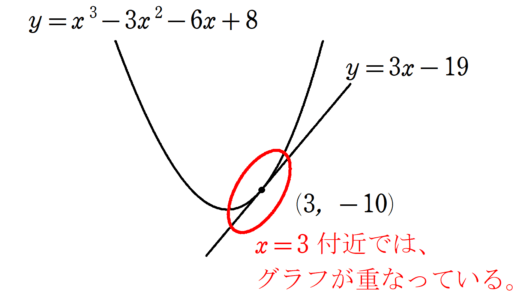
　図４からもわかる通り、接線のとらえ方を変えると、$~x=3~$付近なら、三次関数$~f(x)=x^3-3x^2-6x+8~$は、一次関数$~f(x) = 3x-19~$に近似できると言えます。
 
　さて、例題１の解説の$①$は

f(x)=f(3)+(x-3)f'(3)

とも表せます。
 
　$~3~$を定点$~a~$として捉えると、もとの三次関数は$~x=a~$の付近なら、

f(x)=f(a)+f'(a)(x-a)~~~~\cdots ②

と近似できるということです。

　そして、テイラーの定理を見比べると、$~②~$はテイラー展開の２項目までであることがわかります。
 
　ただ、当然ながら三次関数を一次関数で近似しているので精度は悪いです。

Ⅱー②　３次関数を２次関数で近似する

　一次関数である接線も見方を変えると、$~x=3~$付近の近似式であることがわかりました。
　では、近似の精度を上げるために、今度は２次関数を使って近似してみましょう。
 
　まずは、２次の近似式を作ります。

f(x)=f(a)+f'(a)(x-a)+k_2(x-a)^2

\begin{align*}
f'(x)&=f'(a)+2k_2(x-a) \\
\\
f^{\prime \prime}(x)&=2k_2
\end{align*}

k_2=\frac{f^{\prime \prime}(a)}{2}

f(x)=f(a)+f'(a)(x-a)+\frac{f^{\prime \prime}(a)}{2}(x-a)^2~~~\cdots③

　$~③~$は、テイラーの定理の３項目までとなっていることがわかります。
 
　実際に、先ほどの３次関数を近似してみましょう。

　２次の近似式は$~③~$で作っているので、$~a=3~$を代入するだけです。

f'(x)=3x^2-6x-6

f^{\prime\prime}(x)=6x-6

\begin{align*}
f^{\prime\prime}(3)&=6\cdot 3-6 \\
&=12
\end{align*}

\begin{align*}
f(x)&=f(3)+f'(3)(x-3)+\frac{f^{\prime \prime}(3)}{2}(x-3)^2 \\
\\
&=-10+3(x-3)+\frac{12}{2}(x-3)^2 \\
\\
&=-10+3x-9+6(x^2-6x+9) \\
&=-10+3x-9+6x^2-36x+54 \\
&=6x^2-33x+35
\end{align*}

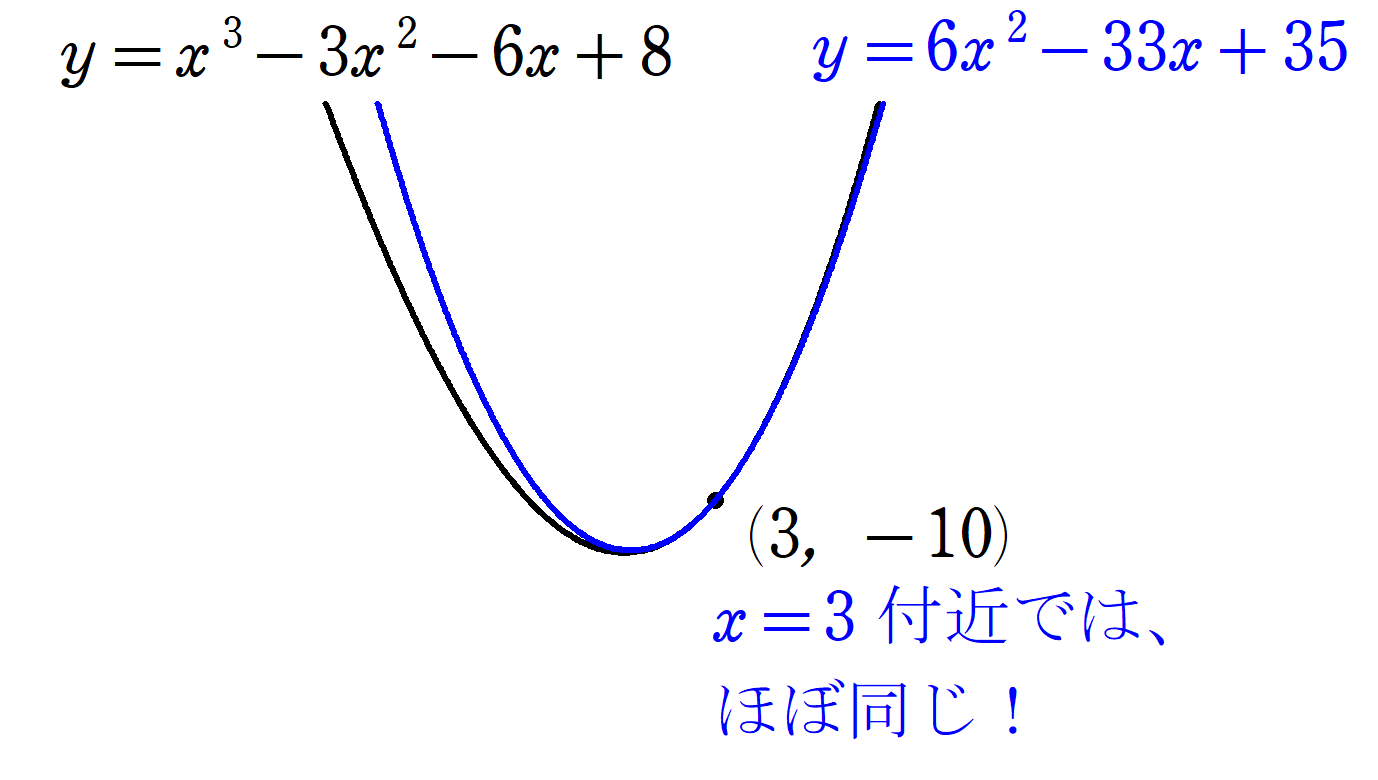
　出来上がった近似式を元のグラフと比べてみましょう。

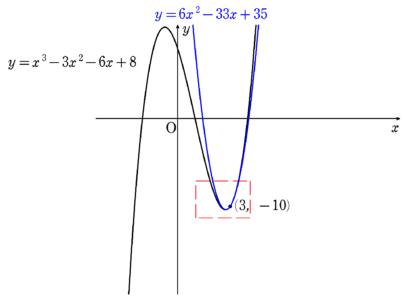
　図５の赤枠内を拡大すると、

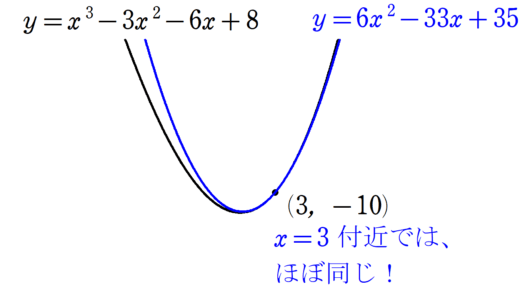
　であり、一次のときよりも格段に精度が上がりました。

Ⅱ－③　n 次関数を(n-1)次関数で近似する

　 ２次の近似式の作り方 を利用し、$~f(x)~$の$~x=a~$付近における$~(n-1)~$次の近似式を作ります。

f(x)=f(a)+f'(a)(x-a)+\frac{f^{\prime \prime}(a)}{2}(x-a)^2+k_3(x-a)^3

\begin{align*}
f'(x)&=f'(a)+f^{\prime \prime}(a)(x-a)+3k_3(x-a)^2 \\
\\
f^{\prime \prime}(x)&=f^{\prime \prime}(a)+3\cdot 2k_3(x-a)  \\
\\
f^{\prime \prime \prime}(x)&=3\cdot 2 k_3  \\
\end{align*}

k_3=\frac{f^{\prime \prime \prime}(a)}{3\cdot 2}

f(x)=f(a)+f'(a)(x-a)+\frac{f^{\prime \prime}(a)}{2}(x-a)^2+\frac{f^{\prime \prime \prime}(a)}{3!}(x-a)^3

\begin{align*}
f(x)&=f(a)+f'(a)(x-a)+\frac{f^{\prime \prime}(a)}{2}(x-a)^2+ \\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+\cdots+\frac{f^{(n-1)}(a)}{(n-1)!}(x-a)^{n-1}~~~\cdots ④
\end{align*}

　ただ、$~x=a~$ならば$~④~$と元の式の値が一致するものの、$~a~$付近なので誤差が出ます。

　テイラーの定理において、その誤差を表したのが剰余項$~\displaystyle R_n=\frac{f^{(n)}(\xi)}{n!}(x-a)^n~$となります。

Ⅱ－④　剰余項の例

　先ほどの３次関数についての誤差（剰余項）を調べてみましょう。
　わかりやすく１次関数（接線）と比較してみます。

三次と一次の剰余項

　$~f(x)=x^3-3x^2-6x+8~$とその１次近似式$~y=3x-19~$の、$~x=4~$における誤差を求める。

　元の三次関数に$~x=4~$を代入すると、

\begin{align*}
f(4)&=4^3-3\cdot 4^2-6\cdot 4+8 \\
&=64-48-24+8 \\
&=0
\end{align*}

であり、一次の近似式に $~x=4~$を代入すると、

\begin{align*}
y&=3\cdot 4-19 \\
&=-7
\end{align*}

となるため、誤差（剰余項）は$~7~$である。

　剰余項の値からを$~\xi~$求める。

　一次の近似式のため、剰余項は$~R_2~$で表される。

R_2=\frac{f^{(2)}(\xi)}{2!}(x-4)^2

　この$~R_2~$から$~\xi~$の値を求めると、

\begin{align*}
\frac{f^{\prime\prime}(\xi)}{2!}(4-3)^2&=7 \\
f^{\prime\prime}(\xi)&=14 \\
6\xi-6&=14 \\
6\xi&=20 \\
\xi&=\frac{10}{3}
\end{align*}

とわかる。

　この例で求まった$~\xi~$の値は、テイラーの定理の条件である$~a=3 < \xi < 4=x~$を満たしています。

　このように、$~n~$次式を、$~x=a~$付近で$~n-1~$次式で近似したときの誤差が剰余項$~R_n~$であることは理解できました。
 
　しかし、なぜ$~\displaystyle R_n=\frac{f^{(n)}(\xi)}{n!}(x-a)^n~$で表されるのかは解決していないため、次章以降でテイラーの定理を直接証明をして、この疑問を解決します。

Ⅲ　テイラーの定理の証明

Ⅲー①　証明の予備知識

　テイラーの定理の証明をするにあたって、「コーシーの平均値の定理」を利用します。

 \frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(c)}{g'(c)}

　この定理の証明は、下の関連記事をご覧ください。

あわせて読みたい

コーシーの平均値の定理 　数学Ⅲで、「平均値の定理」を学びますが、本記事の「コーシーの平均値の定理」は、その一般化ともいえる定理となっています。それを例を交えて解説・証明していきます…

Ⅲー②　テイラーの定理の証明

　証明では、コーシーの平均値の定理を繰り返し使用します。

\begin{align*}
F(x)&=f(x)-\left\{ f(a)+(x-a)\frac{f'(a)}{1!}+\cdots \right.  \\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \left.+(x-a)^{n-1}\frac{f^{(n-1)}(a)}{(n-1)!} \right\}~\cdots ⑤
\end{align*}

\begin{align*}
F(a)&=f(a)-\left\{ f(a)+(a-a)\frac{f'(a)}{1!}+\cdots+(a-a)^{n-1}\frac{f^{(n-1)}(a)}{(n-1)!} \right\}  \\
\\
&=f(a)-f(a)  \\
&=0
\end{align*}

\begin{align*}
F'(x)&=f'(x)-\left\{ 0+\frac{f'(a)}{1!}+2(x-a)\frac{f^{\prime \prime}(a)}{2!}+\cdots \right.  \\
&\left.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+(n-1)(x-a)^{n-2}\frac{f^{(n-1)}(a)}{(n-1)!} \right\} \\
\\
&=f'(x)-\frac{f'(a)}{1!}-(x-a)\frac{f^{\prime \prime}(a)}{1!}-\cdots-(x-a)^{n-2}\frac{f^{(n-1)}(a)}{(n-2)!} 
\end{align*}

F'(a)=f'(a)-f'(a)=0

\begin{align*}
F^{\prime \prime}(x)&=f^{\prime \prime}(x)-0-\frac{f^{\prime \prime}(a)}{1!}-2(x-a)\frac{f^{\prime \prime \prime}(a)}{2!}-\cdots  \\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~-(n-2)(x-a)^{n-3}\frac{f^{(n-1)}(a)}{(n-2)!} \\
\\
&=f^{\prime \prime}(x)-\frac{f^{\prime \prime}(a)}{1!}-(x-a)\frac{f^{\prime \prime \prime}(a)}{1!}-\cdots  \\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~-(x-a)^{n-3}\frac{f^{(n-1)}(a)}{(n-3)!} 
\end{align*}

F^{\prime \prime}(a)=f^{\prime \prime}(a)-f^{\prime \prime}(a)=0

F^{(n-1)}(x)=f^{(n-1)}(x)-\frac{f^{(n-1)}(a)}{1!}

F^{(n-1)}(a)=f^{(n-1)}(a)-f^{(n-1)}(a)=0

F(a)=F'(a)=F^{\prime \prime}(a)=\cdots=F^{(n-1)}(a)=0

F^{(n)}(x)=f^{(n)}(x)-0=f^{(n)}(x)~~~\cdots ⑥

F^{(n)}(a)=f^{(n)}(a)

\frac{F(x)-F(a)}{G(x)-G(a)}=\frac{F'(x_1)}{G'(x_1)}

\frac{F(x)}{G(x)}=\frac{F'(x_1)}{G'(x_1)}~~~\cdots ⑦

\frac{F'(x_1)-F'(a)}{G'(x_1)-G'(a)}=\frac{F^{\prime \prime}(x_2)}{G^{\prime \prime}(x_2)}

\frac{F'(x_1)}{G'(x_1)}=\frac{F^{\prime \prime}(x_2)}{G^{\prime \prime}(x_2)}~~~\cdots ⑧

\frac{F^{(n-1)}(x_{n-1})}{G^{(n-1)}(x_{n-1})}=\frac{F^{(n)}(x_n)}{G^{(n)}(x_n)}~~~\cdots⑨

\frac{F(x)}{G(x)}=\frac{F^{(n)}(x_n)}{G^{(n)}(x_n)}~~~\cdots ⑩

x \lessgtr x_1 \lessgtr x_2 \lessgtr \cdots \lessgtr x_{n-1} \lessgtr x_n \lessgtr a

\begin{align*}
G^{(n)}(x_n)&=n(n-1)(n-2)\cdots 2 \cdot 1 \\
&=n!
\end{align*}

\begin{align*}
\frac{F(x)}{(x-a)^n}&=\frac{f^{(n)}(x_n)}{n!} \\
\\
F(x)&=(x-a)^n \frac{f^{(n)}(x_n)}{n!}~~~\cdots⑪
\end{align*}

\begin{align*}
(x-a)^n \frac{f^{(n)}(\xi)}{n!}&=f(x)-\left\{ f(a)+(x-a)\frac{f'(a)}{1!} +\cdots\right.  \\
 &~~~~~~~~~~~~~~~~~~~~~~~~~~\left. +(x-a)^{n-1}\frac{f^{(n-1)}(a)}{(n-1)!} \right\} \\
\\
f(x)&=f(a)+(x-a)\frac{f'(a)}{1!}  +\cdots\\
&~~~~~~~~~~~~~~~~~~~~+(x-a)^{n-1}\frac{f^{(n-1)}(a)}{(n-1)!}+(x-a)^n \frac{f^{(n)}(\xi)}{n!}
\end{align*}

　剰余項$~R_n=\displaystyle (x-a)^n\frac{f^{(n)}(\xi)}{n!}~$に出てくる$~\xi~$は、コーシーの平均値の定理に由来することがわかりました。

Ⅳ　テイラー級数への拡張

　テイラーの定理を拡張すると、解析学上で非常に重要な公式へと繋がっていきます。

\lim_{n \to \infty}{R_n}=\lim_{n \to \infty}{\frac{f'(\xi)}{n!}(x-a)^n}=0~~~~(x \lessgtr \xi \lessgtr a)

f(x)=f(a)+(x-a)\frac{f'(a)}{1!}+(x-a)^2\frac{f^{\prime\prime}(a)}{2!}+\cdots+(x-a)^n\frac{f^{(n)}(a)}{n!}+\cdots

　テイラーの定理とテイラー級数の相違点として、以下の２点が挙げられます。

• $~f(x)~$の前提が、無限回微分可能になっている。
• 剰余項$~R_n~$が無い代わりに、項が無限に続いている。

　テイラー級数は、テイラーの定理における剰余項（誤差）$~R_n~$が$~0~$に近づく前提の上で、$~f(x)~$が無限和で表されることを主張しています。

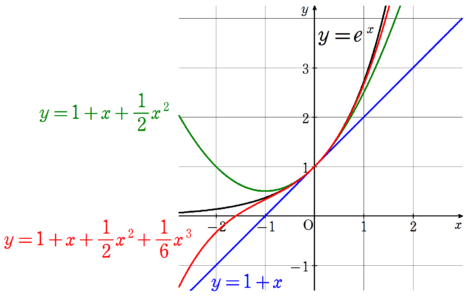
　このテイラー級数の良いところは、$~\sin{x}~$や$~e^x~$のように、$~x~$を代入したときの値が分かりづらい関数も、定点$~a~$のまわりであれば、多項式として近似できることにあります。
　詳しくは以下の記事をご覧ください。

あわせて読みたい

非公開: テイラー級数とマクローリン級数 テイラーの定理からテイラー級数へ、そしてテイラー級数の特殊形であるマクローリン級数について紹介していきます。 【Ⅰ　テイラー級数】 　今回の記事の出発点となるテ…

どうでもいいけど、$~\xi~$書きにくくない？

うん‥‥。
パソコン上（Tex）だと、「\xi」ですぐ書けるんだけどね‥‥。