コーシーの平均値の定理

2020年1月5日2022年12月7日

当ページのリンクには広告が含まれています。

　数学Ⅲで、「平均値の定理」を学びますが、本記事の「コーシーの平均値の定理」は、その一般化ともいえる定理となっています。それを例を交えて解説・証明していきます。

この記事を読んでわかること

コーシーの平均値の定理の内容

　コーシーの平均値の定理は、1823年にコーシーが出版した『エコール・ポリテクニクの無限小解析要論』で、「ラグランジュの平均値の定理」の一般化として述べられています。

※詳しい成立背景については、「ラグランジュの平均値の定理」を参照のこと。
※数学Ⅲで習う「平均値の定理」は、「ラグランジュの平均値の定理」のことです。

ラグランジュの平均値の定理と似ている

コーシーの平均値の定理

　閉区間 $~[a,b]~$ で連続、開区間 $~(a,b)~$ で微分可能な $~f(x) , g(x)~$ に関して、$g(b)-g(a)\neq 0 ~$ならば、

\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(c)}{g'(c)}

を満たす $~c \in (a,b)~$ が存在する。（ただし、$g'(c)\neq 0$）

　先に書いたように、コーシーの平均値の定理は、ラグランジュの平均値の定理の一般化なので、式や条件が酷似しています。

（ラグランジュの）平均値の定理　（参考）

　閉区間 $~[a,b]~$ で連続、開区間 $~(a,b)~$ で微分可能な $~f(x)~$ に関して、

\frac{f(b)-f(a)}{b-a}=f'(c)

を満たす $~c \in (a,b)~$ が存在する。

y=f(x) や y=g(x) では意味をなさない

コーシーの平均値の定理を、具体例で理解してみましょう。

コーシーの平均値の定理の例1

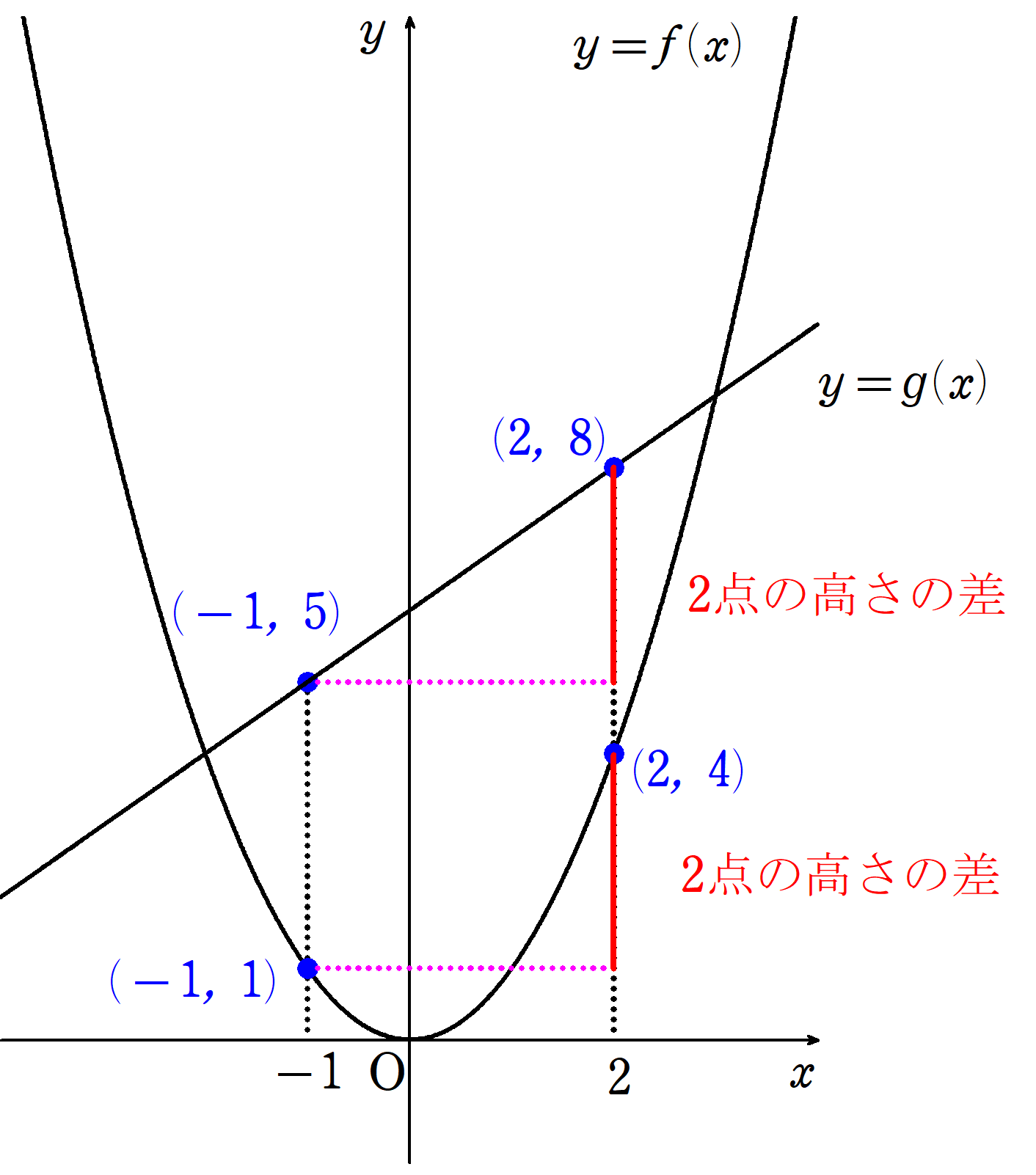
　$~f(x)=x^2~,~g(x)=x+6~~(a=-1,b=2)~$

　$~f(x),g(x)$はそれぞれ閉区間 $~[-1,2]~$ で連続、開区間 $~(-1,2)~$ で微分可能であるため、コーシーの平均値の定理より、

\begin{align*}\frac{f'(c)}{g'(c)}&=\frac{f(2)-f(-1)}{g(2)-g(-1)} \\ \\&=\frac{4-1}{8-5} \\ \\ &=1\end{align*}

を満たす $~c \in (-1,2)~$ が存在する。

　実際、 $~f'(x)=2x~,~g'(x)=1~$ より、 $~\displaystyle \frac{2c}{1}=1 ~$ で、$~c=\displaystyle \frac{1}{2}~$は確かに $~c \in (-1,2)~$ を満たしています。

　ただ、例1からコーシーの平均値の定理の意味を考えてみると、$~\displaystyle \frac{f(2)-f(-1)}{g(2)-g(-1)}~$が意味することは、$f(x)~$と$~g(x)~$上の２点の高さの差の割合です。（図1）

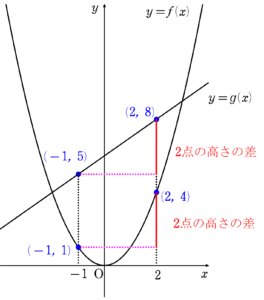
　この高さの差の割合が、$~\displaystyle \frac{f'(c)}{g'(c)}~$と等しい、すなわち$x=c~$における$~f(x)~$と$~g(x)~$の接線の傾きの割合と同じという事実が浮かび上がってきます。

　しかし、高さの差の割合と接線の傾きの割合が同じであることなど、意味があるものとは言えません。

媒介変数表示でこそ意味を持つ

　$~y=f(x)~,~y=g(x)~$としてコーシーの平均値の定理を使った際には興味深い事実が得られなかったものの、媒介変数で表される関数については重要な意味を持ちます。

　具体例でその意味を体感してみましょう。

コーシーの平均値の定理の例2

　$~f(t)=\sin{t} , g(t)=\cos{t}~$$~ \displaystyle \left( a=\frac{1}{6}\pi , b=\frac{5}{6}\pi \right)$

　$~(g(t)~,~f(t))~$で表される曲線は、図2のような扇形の弧となる。

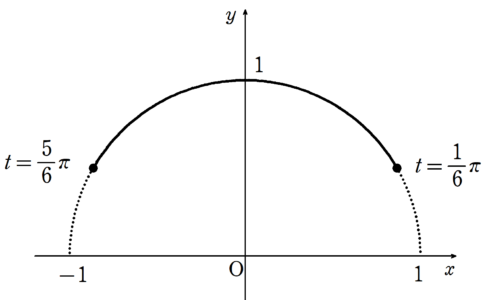
　$~f(t)~,~g(t)~$はそれぞれ閉区間$~\displaystyle \left[\frac{1}{6}\pi ,\frac{5}{6}\pi \right]~$で連続、開区間 $~\displaystyle \left(\frac{1}{6}\pi~,~\frac{5}{6}\pi \right)~$で微分可能であるため、コーシーの平均値の定理より、

\begin{align*} \frac{f'(c)}{g'(c)}&=\frac{f\left( \frac{5}{6}\pi \right)-f \left( \frac{1}{6}\pi \right)}{g\left( \frac{5}{6}\pi \right)-g \left( \frac{1}{6}\pi \right)} \\ \\ &=\frac{\frac{1}{2}-\frac{1}{2}}{-\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}} \\ \\ &=0 \end{align*}

を満たす $~c \in \displaystyle \left(\frac{1}{6}\pi~,~\frac{5}{6}\pi \right)~$ が存在する。

　実際、$~f'(c)=\cos{c}~,~g'(c)=-\sin{c}~$ より、$~\displaystyle \frac{\cos{c}}{-\sin{c}}=0 ~$ で、$~c=\displaystyle \frac{1}{2}\pi~$は確かに $~c \in \displaystyle \left(\frac{1}{6}\pi~,~\frac{5}{6}\pi \right)~$ を満たしています。

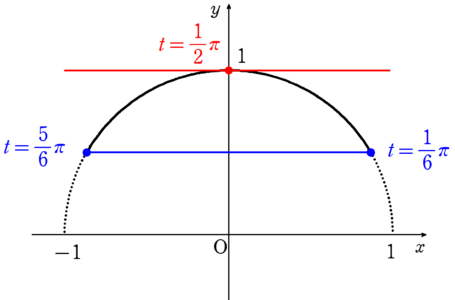
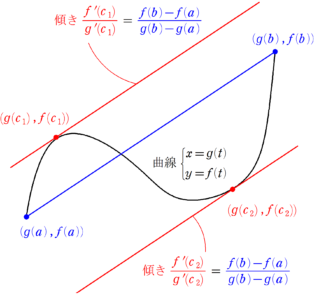
　コーシーの平均値の定理の例2 で、左辺の$~\displaystyle \frac{f(b)-f(a)}{g(b)-g(a)}~$は、端点を結んだ直線の傾き。

　また、右辺についても、以下のように変形できます。

\frac{f'(t)}{g'(t)}=\frac{\frac{df}{dt}}{\frac{df}{dt}}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{dy}{dx}

　つまり、コーシーの平均値の定理とは、ラグランジュの平均値の定理を、媒介変数表示で使える形にしたものと言えるのです。

コーシーの平均値の定理の証明

　証明は、ラグランジュの平均値の定理と同様の方法で可能です。

コーシーの平均値の定理の証明

　$~F(x)=f(x)+Ag(x)~$とおき、$~F(a)=F(b)~$となりような定数$~A ~$をまずは求める。

　$~F(a)=f(a)+Ag(a)~$、$~F(b)=f(b)+Ag(b)~$より、

\begin{align*} f(a)+Ag(a)&=f(b)+Ag(b) \\ -Ag(b)+Ag(a)&=f(b)-f(a) \\ -A{ g(b)-g(a) }&=f(b)-f(a) \\ A&=-\frac{f(b)-f(a)}{g(b)-g(a)} \end{align*}

が求まった。（ただし、$~g(b)-g(a) \neq 0~$）

　次に、この$~\displaystyle F(x)=f(x)-\frac{f(b)-f(a)}{g(b)-g(a)}g(x)~$について考える。

　$~~ f(x)~$と$~g(x)~$が閉区間 $~[a,b]~$ で連続、開区間 $~(a,b)~$ で微分可能であるため、$~x~$で両辺を微分することで