数学Ⅰの三角比では、$~\displaystyle \sin{30^{\circ}}=\frac{1}{2}~$や$~\displaystyle \cos{45^{\circ}}=\frac{1}{\sqrt{2}}~$のような三角定規に登場する角(有名角)を扱います。
では有名角以外で、近似値を使わずに値が出る角はあるのでしょうか?
実は、$~36^{\circ}~$や$~22.5^{\circ}~$などの三角比も値を正確に出すことができます。
この記事では、それらのマイナーな角度の三角比を含めた三角比の表を掲載。
個別ページでは、マイナーな角度の三角比の値の求め方をそれぞれ解説しているので、値だけでなく導出過程まで理解することができます。
- 0°~45°の三角比の値
- 45°~360°の三角比の値
- 3の倍数の角度であれば、三角比の値は出せる
0°~45°の三角比
いろいろな角度の三角比の値を出すにあたって、必要なのは0°以上45°未満の角度のみです。
というのも、三角比には様々な変換公式があるため、0°~45°の三角比さえわかっていれば、45°~360°は計算により求めることができます。(後述)
0°~45°の中で、近似値を使わずに三角比の値が出せるものは、下の表1の通りです。
| $~\theta~$ | $~\sin{\theta}~$ | $~\cos{\theta}~$ | $~\tan{\theta}~$ |
| $~\displaystyle 0^{\circ}\left( =0 \right)~$ | $~\displaystyle 0~$ | $~\displaystyle 1~$ | $~\displaystyle 0~$ |
| $~\displaystyle 15^{\circ}\left(=\frac{\pi}{12}\right)~$ | $~\displaystyle \frac{\sqrt{6}-\sqrt{2}}{4}~$ | $~\displaystyle \frac{\sqrt{6}+\sqrt{2}}{4}~$ | $~\displaystyle 2-\sqrt{3}~$ |
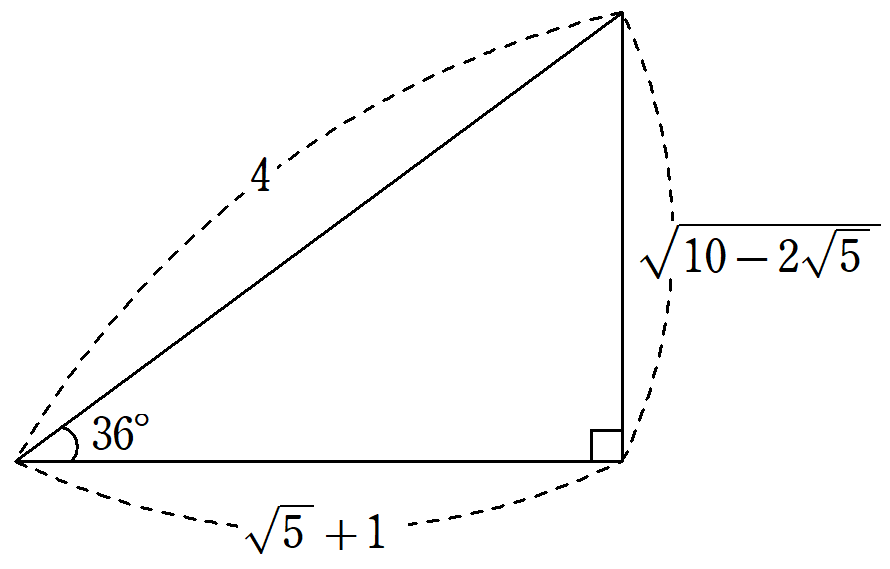
| $~\displaystyle 18^{\circ}\left(=\frac{\pi}{10}\right)~$ | $~\displaystyle \frac{\sqrt{5}-1}{4}~$ | $~\displaystyle \frac{\sqrt{10+2\sqrt{5}}}{4}~$ | $~\displaystyle \frac{\sqrt{25-10\sqrt{5}}}{5}~$ |
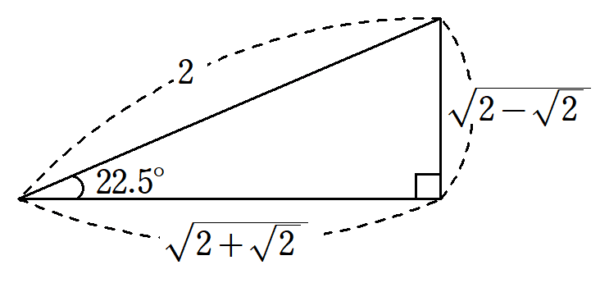
| $~\displaystyle 22.5^{\circ}\left(=\frac{\pi}{8}\right)~$ | $~\displaystyle \frac{2-\sqrt{2}}{2}~$ | $~\displaystyle \frac{2+\sqrt{2}}{2}~$ | $~\displaystyle \sqrt{2}-1~$ |
| $~\displaystyle 30^{\circ}\left(=\frac{\pi}{6}\right)~$ | $~\displaystyle \frac{1}{2}~$ | $~\displaystyle \frac{\sqrt{3}}{2}~$ | $~\displaystyle \frac{\sqrt{3}}{3}~$ |
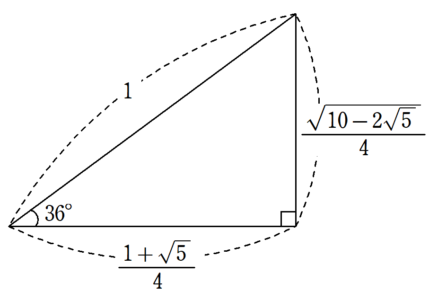
| $~\displaystyle 36^{\circ}\left(=\frac{\pi}{5}\right)~$ | $~\displaystyle \frac{\sqrt{10-2\sqrt{5}}}{4}~$ | $~\displaystyle \frac{\sqrt{5}+1}{4}~$ | $~\displaystyle \sqrt{5-2\sqrt{5}}~$ |
| $~\displaystyle 45^{\circ}\left(=\frac{\pi}{4}\right)~$ | $~\displaystyle \frac{\sqrt{2}}{2}~$ | $~\displaystyle \frac{\sqrt{2}}{2}~$ | $~\displaystyle 1~$ |
$~0^{\circ}~,~30^{\circ}~,~45^{\circ}~$に関しては、数学Ⅰで学びますが、他の角度については通常学ぶことはありません。
しかし、$~15^{\circ}~,~18^{\circ}~,~22.5^{\circ}~,~36^{\circ}~$のいずれも、数学Ⅰまでの知識で求めることができます。
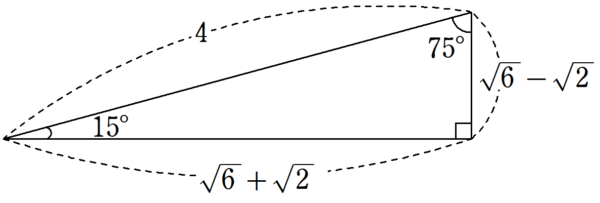
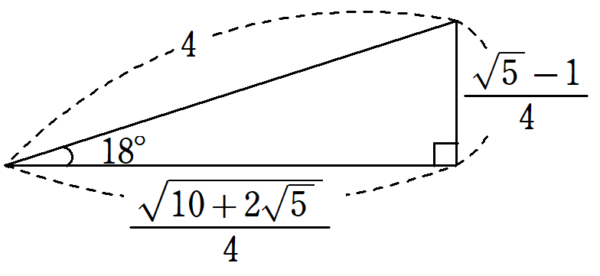
45°~360°の三角比
0°~45°の三角比の値がわかれば、数学Ⅰや数学Ⅱで登場する公式を使って、残りの角度は変換することができます。
45°~90°の三角比
使う公式は、数学Ⅰで学ぶ以下の公式。
\begin{align*}
\sin{(90^{\circ}-\theta)}&=\cos{\theta} \\
\cos{(90^{\circ}-\theta)}&=\sin{\theta} \\
\tan{(90^{\circ}-\theta)}&=\frac{1}{\tan{\theta}} \\
\end{align*}この$~90^{\circ}-\theta~$の三角比を使うことで、
\sin{54^{\circ}}=\sin{(90^{\circ}-36^{\circ})}=\cos{36^{\circ}} のように、45°~90°の三角比を求めることができます。
実際に変換したのが、次の表2です。
| $~\theta~$ | $~\sin{\theta}~$ | $~\cos{\theta}~$ | $~\tan{\theta}~$ |
| $~\displaystyle 45^{\circ}\left(=\frac{\pi}{4}\right)~$ | $~\displaystyle \frac{\sqrt{2}}{2}~$ | $~\displaystyle \frac{\sqrt{2}}{2}~$ | $~\displaystyle 1~$ |
| $~\displaystyle 54^{\circ}\left(=\frac{3\pi}{10}\right)~$ | $~\displaystyle \frac{\sqrt{5}+1}{4}~$ | $~\displaystyle \frac{\sqrt{10-2\sqrt{5}}}{4}~$ | $~\displaystyle \frac{\sqrt{25+10\sqrt{5}}}{5}~$ |
| $~\displaystyle 60^{\circ}\left(=\frac{\pi}{3}\right)~$ | $~\displaystyle \frac{\sqrt{3}}{2}~$ | $~\displaystyle \frac{1}{2}~$ | $~\displaystyle \sqrt{3}~$ |
| $~\displaystyle 67.5^{\circ}\left(=\frac{3\pi}{8}\right)~$ | $~\displaystyle \frac{2+\sqrt{2}}{2}~$ | $~\displaystyle \frac{2-\sqrt{2}}{2}~$ | $~\displaystyle \sqrt{2}+1~$ |
| $~\displaystyle 72^{\circ}\left(=\frac{2\pi}{5}\right)~$ | $~\displaystyle \frac{\sqrt{10+2\sqrt{5}}}{4}~$ | $~\displaystyle \frac{\sqrt{5}-1}{4}~$ | $~\displaystyle \sqrt{5+2\sqrt{5}}~$ |
| $~\displaystyle 75^{\circ}\left(=\frac{5\pi}{12}\right)~$ | $~\displaystyle \frac{\sqrt{6}+\sqrt{2}}{4}~$ | $~\displaystyle \frac{\sqrt{6}-\sqrt{2}}{4}~$ | $~\displaystyle 2+\sqrt{3}~$ |
| $~\displaystyle 90^{\circ}\left(=\frac{\pi}{2}\right)~$ | $~\displaystyle 1~$ | $~0~$ | なし |
90°~180°の三角比
これで 0°~90° の三角比の値がわかったため、次は180°まで拡張します。
\begin{align*}
\sin{(180^{\circ}-\theta)}&=\sin{\theta} \\
\cos{(180^{\circ}-\theta)}&=-\cos{\theta} \\
\tan{(180^{\circ}-\theta)}&=-\tan{\theta} \\
\end{align*}この$~180^{\circ}-\theta~$の三角比を使うことで、
\sin{112.5^{\circ}}=\sin{(180^{\circ}-67.5^{\circ})}=\sin{67.5^{\circ}} のように、90°~180°の三角比を求めることができます。
実際に変換したのが、次の表3です。
| $~\theta~$ | $~\sin{\theta}~$ | $~\cos{\theta}~$ | $~\tan{\theta}~$ |
| $~\displaystyle 90^{\circ}\left(=\frac{\pi}{2}\right)~$ | $~\displaystyle 1~$ | $~0~$ | なし |
| $~\displaystyle 105^{\circ}\left(=\frac{7\pi}{12}\right)~$ | $~\displaystyle \frac{\sqrt{6}+\sqrt{2}}{4}~$ | $~\displaystyle -\frac{\sqrt{6}-\sqrt{2}}{4}~$ | $~\displaystyle -2-\sqrt{3}~$ |
| $~\displaystyle 108^{\circ}\left(=\frac{3\pi}{5}\right)~$ | $~\displaystyle \frac{\sqrt{10+2\sqrt{5}}}{4}~$ | $~\displaystyle -\frac{\sqrt{5}-1}{4}~$ | $~\displaystyle -\sqrt{5+2\sqrt{5}}~$ |
| $~\displaystyle 112.5^{\circ}\left(=\frac{5\pi}{8}\right)~$ | $~\displaystyle \frac{2+\sqrt{2}}{2}~$ | $~\displaystyle -\frac{2-\sqrt{2}}{2}~$ | $~\displaystyle -\sqrt{2}-1~$ |
| $~\displaystyle 120^{\circ}\left(=\frac{2\pi}{3}\right)~$ | $~\displaystyle \frac{\sqrt{3}}{2}~$ | $~\displaystyle -\frac{1}{2}~$ | $~\displaystyle -\sqrt{3}~$ |
| $~\displaystyle 126^{\circ}\left(=\frac{7\pi}{10}\right)~$ | $~\displaystyle \frac{\sqrt{5}+1}{4}~$ | $~\displaystyle -\frac{\sqrt{10-2\sqrt{5}}}{4}~$ | $~\displaystyle -\frac{\sqrt{25+10\sqrt{5}}}{5}~$ |
| $~\displaystyle 135^{\circ}\left(=\frac{3\pi}{4}\right)~$ | $~\displaystyle \frac{\sqrt{2}}{2}~$ | $~\displaystyle -\frac{\sqrt{2}}{2}~$ | $~\displaystyle -1~$ |
| $~\displaystyle 144^{\circ}\left(=\frac{4\pi}{5}\right)~$ | $~\displaystyle \frac{\sqrt{10-2\sqrt{5}}}{4}~$ | $~\displaystyle -\frac{\sqrt{5}+1}{4}~$ | $~\displaystyle -\sqrt{5-2\sqrt{5}}~$ |
| $~\displaystyle 150^{\circ}\left(=\frac{5\pi}{6}\right)~$ | $~\displaystyle \frac{1}{2}~$ | $~\displaystyle -\frac{\sqrt{3}}{2}~$ | $~\displaystyle -\frac{\sqrt{3}}{3}~$ |
| $~\displaystyle 157.5^{\circ}\left(=\frac{7\pi}{8}\right)~$ | $~\displaystyle \frac{2-\sqrt{2}}{2}~$ | $~\displaystyle -\frac{2+\sqrt{2}}{2}~$ | $~\displaystyle -\sqrt{2}+1~$ |
| $~\displaystyle 162^{\circ}\left(=\frac{9\pi}{10}\right)~$ | $~\displaystyle \frac{\sqrt{5}-1}{4}~$ | $~\displaystyle -\frac{\sqrt{10+2\sqrt{5}}}{4}~$ | $~\displaystyle -\frac{\sqrt{25-10\sqrt{5}}}{5}~$ |
| $~\displaystyle 165^{\circ}\left(=\frac{11\pi}{12}\right)~$ | $~\displaystyle \frac{\sqrt{6}-\sqrt{2}}{4}~$ | $~\displaystyle -\frac{\sqrt{6}+\sqrt{2}}{4}~$ | $~\displaystyle -2+\sqrt{3}~$ |
| $~\displaystyle 180^{\circ}\left(=\pi \right)~$ | $~\displaystyle 0~$ | $~\displaystyle 1~$ | $~\displaystyle 0~$ |
180°~360°の三角比
最後は、数学Ⅱで出てくる公式を使います。
\begin{align*}
\sin{(180^{\circ}+\theta)}&=-\sin{\theta} \\
\cos{(180^{\circ}+\theta)}&=-\cos{\theta} \\
\tan{(180^{\circ}+\theta)}&=\tan{\theta} \\
\end{align*}この$~180^{\circ}+\theta~$の三角比を使うことで、
\sin{285^{\circ}}=\sin{(180^{\circ}+105^{\circ})}=-\sin{105^{\circ}} のように、180°~360°の三角比を求めることができます。
実際に変換したのが、次の表4です。
| $~\theta~$ | $~\sin{\theta}~$ | $~\cos{\theta}~$ | $~\tan{\theta}~$ |
| $~\displaystyle 180^{\circ}\left( =\pi \right)~$ | $~\displaystyle 0~$ | $~\displaystyle -1~$ | $~\displaystyle 0~$ |
| $~\displaystyle 195^{\circ}\left(=\frac{13\pi}{12}\right)~$ | $~\displaystyle -\frac{\sqrt{6}-\sqrt{2}}{4}~$ | $~\displaystyle -\frac{\sqrt{6}+\sqrt{2}}{4}~$ | $~\displaystyle 2-\sqrt{3}~$ |
| $~\displaystyle 198^{\circ}\left(=\frac{11\pi}{10}\right)~$ | $~\displaystyle -\frac{\sqrt{5}-1}{4}~$ | $~\displaystyle -\frac{\sqrt{10+2\sqrt{5}}}{4}~$ | $~\displaystyle \frac{\sqrt{25-10\sqrt{5}}}{5}~$ |
| $~\displaystyle 202.5^{\circ}\left(=\frac{9\pi}{8}\right)~$ | $~\displaystyle -\frac{2-\sqrt{2}}{2}~$ | $~\displaystyle -\frac{2+\sqrt{2}}{2}~$ | $~\displaystyle \sqrt{2}-1~$ |
| $~\displaystyle 210^{\circ}\left(=\frac{7\pi}{6}\right)~$ | $~\displaystyle -\frac{1}{2}~$ | $~\displaystyle -\frac{\sqrt{3}}{2}~$ | $~\displaystyle \frac{\sqrt{3}}{3}~$ |
| $~\displaystyle 216^{\circ}\left(=\frac{6\pi}{5}\right)~$ | $~\displaystyle -\frac{\sqrt{10-2\sqrt{5}}}{4}~$ | $~\displaystyle -\frac{\sqrt{5}+1}{4}~$ | $~\displaystyle \sqrt{5-2\sqrt{5}}~$ |
| $~\displaystyle 225^{\circ}\left(=\frac{5\pi}{4}\right)~$ | $~\displaystyle -\frac{\sqrt{2}}{2}~$ | $~\displaystyle -\frac{\sqrt{2}}{2}~$ | $~\displaystyle 1~$ |
| $~\displaystyle 234^{\circ}\left(=\frac{13\pi}{10}\right)~$ | $~\displaystyle -\frac{\sqrt{5}+1}{4}~$ | $~\displaystyle -\frac{\sqrt{10-2\sqrt{5}}}{4}~$ | $~\displaystyle \frac{\sqrt{25+10\sqrt{5}}}{5}~$ |
| $~\displaystyle 240^{\circ}\left(=\frac{4\pi}{3}\right)~$ | $~\displaystyle -\frac{\sqrt{3}}{2}~$ | $~\displaystyle -\frac{1}{2}~$ | $~\displaystyle \sqrt{3}~$ |
| $~\displaystyle 247.5^{\circ}\left(=\frac{11\pi}{8}\right)~$ | $~\displaystyle -\frac{2+\sqrt{2}}{2}~$ | $~\displaystyle -\frac{2-\sqrt{2}}{2}~$ | $~\displaystyle \sqrt{2}+1~$ |
| $~\displaystyle 252^{\circ}\left(=\frac{7\pi}{5}\right)~$ | $~\displaystyle -\frac{\sqrt{10+2\sqrt{5}}}{4}~$ | $~\displaystyle -\frac{\sqrt{5}-1}{4}~$ | $~\displaystyle \sqrt{5+2\sqrt{5}}~$ |
| $~\displaystyle 255^{\circ}\left(=\frac{17\pi}{12}\right)~$ | $~\displaystyle -\frac{\sqrt{6}+\sqrt{2}}{4}~$ | $~\displaystyle -\frac{\sqrt{6}-\sqrt{2}}{4}~$ | $~\displaystyle 2+\sqrt{3}~$ |
| $~\displaystyle 270^{\circ}\left(=\frac{3\pi}{2}\right)~$ | $~\displaystyle -1~$ | $~\displaystyle 0~$ | なし |
| $~\displaystyle 285^{\circ}\left(=\frac{19\pi}{12}\right)~$ | $~\displaystyle -\frac{\sqrt{6}+\sqrt{2}}{4}~$ | $~\displaystyle \frac{\sqrt{6}-\sqrt{2}}{4}~$ | $~\displaystyle -2-\sqrt{3}~$ |
| $~\displaystyle 288^{\circ}\left(=\frac{8\pi}{5}\right)~$ | $~\displaystyle -\frac{\sqrt{10+2\sqrt{5}}}{4}~$ | $~\displaystyle \frac{\sqrt{5}-1}{4}~$ | $~\displaystyle -\sqrt{5+2\sqrt{5}}~$ |
| $~\displaystyle 292.5^{\circ}\left(=\frac{13\pi}{8}\right)~$ | $~\displaystyle -\frac{2+\sqrt{2}}{2}~$ | $~\displaystyle \frac{2-\sqrt{2}}{2}~$ | $~\displaystyle -\sqrt{2}-1~$ |
| $~\displaystyle 300^{\circ}\left(=\frac{5\pi}{3}\right)~$ | $~\displaystyle -\frac{\sqrt{3}}{2}~$ | $~\displaystyle \frac{1}{2}~$ | $~\displaystyle -\sqrt{3}~$ |
| $~\displaystyle 306^{\circ}\left(=\frac{17\pi}{10}\right)~$ | $~\displaystyle -\frac{\sqrt{5}+1}{4}~$ | $~\displaystyle \frac{\sqrt{10-2\sqrt{5}}}{4}~$ | $~\displaystyle -\frac{\sqrt{25+10\sqrt{5}}}{5}~$ |
| $~\displaystyle 315^{\circ}\left(=\frac{7\pi}{4}\right)~$ | $~\displaystyle -\frac{\sqrt{2}}{2}~$ | $~\displaystyle \frac{\sqrt{2}}{2}~$ | $~\displaystyle -1~$ |
| $~\displaystyle 324^{\circ}\left(=\frac{9\pi}{5}\right)~$ | $~\displaystyle -\frac{\sqrt{10-2\sqrt{5}}}{4}~$ | $~\displaystyle \frac{\sqrt{5}+1}{4}~$ | $~\displaystyle -\sqrt{5-2\sqrt{5}}~$ |
| $~\displaystyle 330^{\circ}\left(=\frac{11\pi}{6}\right)~$ | $~\displaystyle -\frac{1}{2}~$ | $~\displaystyle \frac{\sqrt{3}}{2}~$ | $~\displaystyle -\frac{\sqrt{3}}{3}~$ |
| $~\displaystyle 337.5^{\circ}\left(=\frac{15\pi}{8}\right)~$ | $~\displaystyle -\frac{2-\sqrt{2}}{2}~$ | $~\displaystyle \frac{2+\sqrt{2}}{2}~$ | $~\displaystyle -\sqrt{2}+1~$ |
| $~\displaystyle 342^{\circ}\left(=\frac{19\pi}{10}\right)~$ | $~\displaystyle -\frac{\sqrt{5}-1}{4}~$ | $~\displaystyle \frac{\sqrt{10+2\sqrt{5}}}{4}~$ | $~\displaystyle -\frac{\sqrt{25-10\sqrt{5}}}{5}~$ |
| $~\displaystyle 345^{\circ}\left(=\frac{23\pi}{12}\right)~$ | $~\displaystyle -\frac{\sqrt{6}-\sqrt{2}}{4}~$ | $~\displaystyle \frac{\sqrt{6}+\sqrt{2}}{4}~$ | $~\displaystyle -2+\sqrt{3}~$ |
| $~\displaystyle 360^{\circ}\left( =2\pi \right)~$ | $~\displaystyle 0~$ | $~\displaystyle 1~$ | $~\displaystyle 0~$ |
3の倍数の角度であれば、三角比の値は出せる
ここからはオマケになりますが、これまでに出てきた三角比の値を組み合わせることで、3の倍数の角度の三角比の値を求めることができます。
3°の三角比の値
例として、$~15^{\circ}~$と$~18^{\circ}~$の三角比の値を、三角関数の加法定理で組み合わせることで、$~3^{\circ}~$の三角比の値を求めることができます。
\begin{align*}
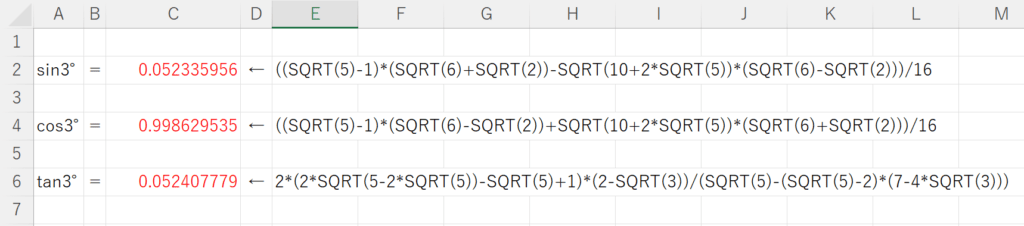
\sin{3^{\circ}}&=\frac{(\sqrt{5}-1)(\sqrt{6}+\sqrt{2})-\sqrt{10+2\sqrt{5}}(\sqrt{6}-\sqrt{2})}{16} \\
\\
\cos{3^{\circ}}&=\frac{(\sqrt{5}-1)(\sqrt{6}-\sqrt{2})-\sqrt{10+2\sqrt{5}}(\sqrt{6}+\sqrt{2})}{16} \\
\\
\tan{3^{\circ}}&=\frac{2(2\sqrt{5-2\sqrt{5}}-\sqrt{5}+1)(2-\sqrt{3})}{\sqrt{5}-(\sqrt{5}-2)(7-4\sqrt{3})}
\end{align*}本当に値が正しいのかを検証するために、Excelで計算をしてみると、以下の<図5>のようになります。
求め方の概要は以下の通り。
\sin{3^{\circ}}=\sin{(18^{\circ}-15^{\circ})}=\sin{18^\circ}\cos{15^{\circ}}+\cos{18^\circ}\sin{15^{\circ}}三角関数の加法定理を使うことで、3°の三角比を求めることができます。
3の倍数の角度の作り方
実際、以下のような組み合わせ方で、値を求めることができます。
\begin{align*}
3^{\circ}&=18^{\circ}-15^{\circ}\\
6^{\circ}&=36^{\circ}-30^{\circ}\\
9^{\circ}&=45^{\circ}-36^{\circ}\\
12^{\circ}&=30^{\circ}-18^{\circ}\\
15^{\circ}& \cdots既知\\
18^{\circ}& \cdots既知\\
21^{\circ}&=36^{\circ}-15^{\circ}\\
24^{\circ}&=54^{\circ}-30^{\circ}\\
27^{\circ}&=45^{\circ}-18^{\circ}\\
30^{\circ}& \cdots既知\\
33^{\circ}&=15^{\circ}+18^{\circ}\\
36^{\circ}& \cdots既知\\
39^{\circ}&=54^{\circ}-15^{\circ}\\
42^{\circ}&=60^{\circ}-18^{\circ}\\
45^{\circ}& \cdots既知\\
\end{align*} もちろん、他の組み合わせ方もありますし、2倍角や3倍角の公式を使っても求まります。
また、$~90^{\circ}-\theta~$の三角比などの公式を使えば、3の倍数の角度すべてについて、三角比の値を求めることができます。
ただ、3°の三角比を見てわかるように、複雑な式が出てくるので、覚悟して計算しましょう。

もし、$~22.5^{\circ}~$の三角比まで利用すれば、$~22.5^{\circ}-18^{\circ}=4.5^{\circ}~$の三角比の値とかも求まるってこと?



うん。そういうことになるね。計算したくはないけど‥‥。
コメント