分子が$~1~$の分数を単位分数といい、分数を単位分数の和で表すことを単位分数分解といいます。
例えば、$~\displaystyle \frac{2}{9}~$であれば、
\frac{2}{9}=\frac{1}{6}+\frac{1}{18} \\といった形で単位分数分解できますが、実は
\begin{align*}
\frac{2}{9}&=\frac{1}{5}+\frac{1}{45} \\
\\
\frac{2}{9}&=\frac{1}{8}+\frac{1}{12}+\frac{1}{72} \\
\end{align*}という形にも単位分数分解できます。
このように、単位分数分解は無限通りにでき、さらにどんな分数でもそれが可能ということが知られています。
この記事では、単位分数分解のやり方だけでなく、なぜどんな分数も無限通りに分解できるのかまで解説!
単位分数分解の利点についても触れています。
単位分数分解とは?
単位分数分解と一口に言っても、その定義は決まっていません。
まずは、この記事で扱う単位分数分解の定義の確認を行います。
異なる単位分数の和で表すこと
単位分数分解は、単位分数(分子が$~1~$の分数)に分解していくことを指しますが、通例一定のルールが存在します。
分数を、異なる単位分数の和で表すことを単位分数分解という。
例を2つほど挙げてみます。
(1) $~\displaystyle \frac{5}{6}~$の単位分数分解
\frac{5}{6}=\frac{1}{2}+\frac{1}{3}(2) $~\displaystyle \frac{1}{2}~$の単位分数分解
\frac{1}{2}=\frac{1}{4}+\frac{1}{5}+\frac{1}{20}先ほどの定義の中で、「異なる単位分数」とあったため、
\frac{1}{2}=\frac{1}{4}+\frac{1}{4}のような分解は不可です。(右辺が$~\displaystyle \frac{2}{4}~$で単位分数でなくなってしまうから)
また、$~\displaystyle \frac{5}{6}~$に関しては、$~\displaystyle \frac{1}{2}~$の分解を代入することで、以下のようにも分解できます。
\frac{5}{6}=\frac{1}{4}+\frac{1}{5}+\frac{1}{20}+\frac{1}{3}実は、単位分数分解の方法は無限通りあり、証明することも可能です。
単位分数分解で平等にパンを分けられる
単位分数分解の方法や無限通りの証明に入る前に、単位分数分解の生活上の利点についても触れておきましょう。
単位分数分解を使うことで、物を本当の意味で平等に分けることができます。
例として、9個のパンを10人で分けることを考えてみましょう。
普通に考えれば、1人あたり$~\displaystyle \frac{9}{10}~$個ですが、これでは平等に分けることはできません。
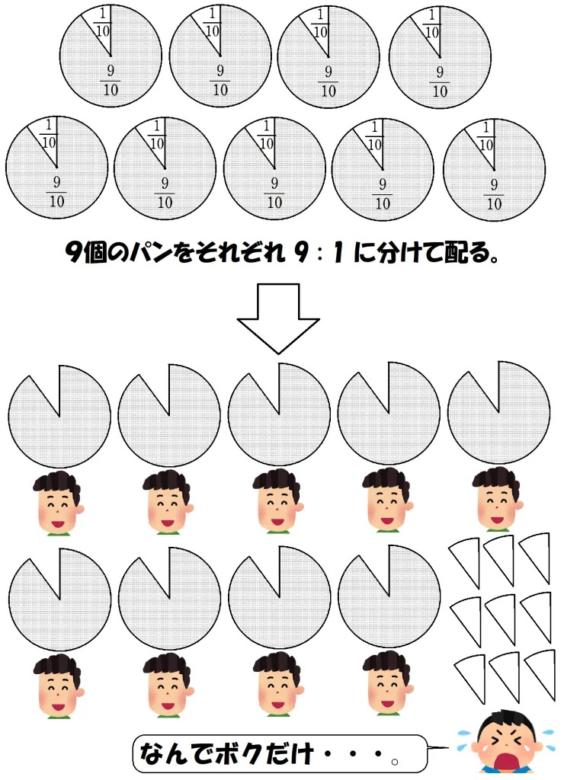
そこで役に立つのが単位分数分解。
$~\displaystyle \frac{9}{10}~$は以下のように単位分数分解ができます。
\frac{9}{10}=\frac{1}{2}+\frac{1}{3}+\frac{1}{15}この式変形をパンに置き換えると、形まで平等に分けることができました。
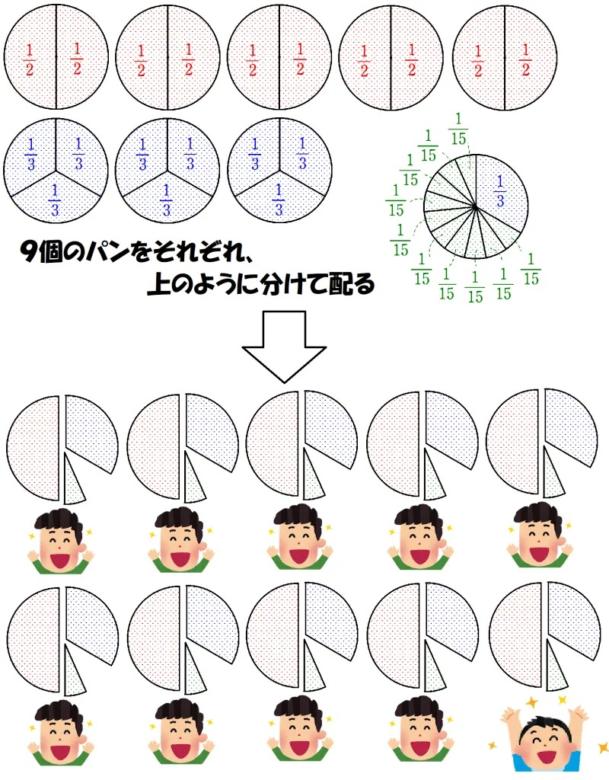
これは、紀元前1650年頃のエジプトの資料「リンド・パピルス」に書かれていた問題であり、単位分数分解が生活に役立っていたことがわかります。

単位分数分解の方法
単位分数分解の方法は、2通りあります。
それぞれについて、例を示しながら解説していきます。
方法①:最大の単位分数をひいていく
1つ目の方法は、機械的に分解していく方法です。
① もとの分数から、それより小さい最大の単位分数をひく。
② その結果が単位分数なら終了。単位分数でないなら、その分数より小さい最大の単位分数をひく。
③ ②を繰り返す。
言葉だけの説明だとわかりづらいので、例を4つほど挙げます。
(1) $~\displaystyle \frac{1}{4}~$の単位分数分解
① $~\displaystyle \frac{1}{4}~$より小さい最大の単位分数は、$~\displaystyle \frac{1}{5}~$なので、
\begin{align*}
\frac{1}{4}-\frac{1}{5}&=\frac{1}{20} \\
\\
\therefore ~~~ \frac{1}{4}&=\frac{1}{5}+\frac{1}{20}
\end{align*}② $~\displaystyle \frac{1}{20}~$は単位分数のため、分解終了。
(2) $~\displaystyle \frac{2}{11}~$の単位分数分解
① $~\displaystyle \frac{2}{11}=\frac{1}{5.5}~$より小さい最大の単位分数は、$~\displaystyle \frac{1}{6}~$なので、
\begin{align*}
\frac{2}{11}-\frac{1}{6}&=\frac{1}{66} \\
\\
\therefore ~~~ \frac{2}{11}&=\frac{1}{6}+\frac{1}{66}
\end{align*}② $~\displaystyle \frac{1}{66}~$は単位分数のため、分解終了。
(3) $~\displaystyle \frac{9}{10}~$の単位分数分解
① $~\displaystyle \frac{9}{10}=\frac{1}{1.11\cdots}~$より小さい最大の単位分数は、$~\displaystyle \frac{1}{2}~$なので、
\begin{align*}
\frac{9}{10}-\frac{1}{2}&=\frac{2}{5} \\
\\
\therefore ~~~ \frac{9}{10}&=\frac{1}{2}+\frac{2}{5}
\end{align*}② $~\displaystyle \frac{2}{5}~$は単位分数ではない。
$~\displaystyle \frac{2}{5}=\frac{1}{2.5}~$より小さい最大の単位分数は$~\displaystyle \frac{1}{3}~$なので、
\begin{align*}
\frac{2}{5}-\frac{1}{3}&=\frac{1}{15} \\
\\
\therefore ~~~ \frac{2}{5}&=\frac{1}{3}+\frac{1}{15}
\end{align*}③ $~\displaystyle \frac{1}{15}~$は単位分数のため、分解終了。
②で出た式を①に代入して、
\frac{9}{10}=\frac{1}{2}+\frac{1}{3}+\frac{1}{15}が得られる。
(4) $~\displaystyle \frac{97}{99}~$の単位分数分解
① $~\displaystyle \frac{97}{99}=\frac{1}{1.02\cdots}~$より小さい最大の単位分数は、$~\displaystyle \frac{1}{2}~$なので、
\begin{align*}
\frac{97}{99}-\frac{1}{2}&=\frac{95}{198} \\
\\
\therefore ~~~ \frac{97}{99}&=\frac{1}{2}+\frac{95}{198}
\end{align*}② $~\displaystyle \frac{95}{198}~$は単位分数ではない。
$~\displaystyle \frac{95}{198}=\frac{1}{2.08\cdots}~$より小さい最大の単位分数は$~\displaystyle \frac{1}{3}~$なので、
\begin{align*}
\frac{95}{198}-\frac{1}{3}&=\frac{29}{198} \\
\\
\therefore ~~~ \frac{95}{198}&=\frac{1}{3}+\frac{29}{198}
\end{align*}③ $~\displaystyle \frac{29}{198}~$は単位分数ではない。
$~\displaystyle \frac{29}{198}=\frac{1}{6.82\cdots}~$より小さい最大の単位分数は$~\displaystyle \frac{1}{7}~$なので、
\begin{align*}
\frac{29}{198}-\frac{1}{7}&=\frac{5}{1386} \\
\\
\therefore ~~~ \frac{29}{198}&=\frac{1}{7}+\frac{5}{1386}
\end{align*}④ $~\displaystyle \frac{5}{1386}~$は単位分数ではなく、$~\displaystyle \frac{5}{1386}=\frac{1}{277.2}~$より小さい最大の単位分数は$~\displaystyle \frac{1}{278}~$なので、
\begin{align*}
\frac{5}{1386}-\frac{1}{278}&=\frac{1}{96327} \\
\\
\therefore ~~~ \frac{5}{1386}&=\frac{1}{278}+\frac{1}{96327}
\end{align*}⑤ $~\displaystyle \frac{1}{96327}~$は単位分数のため、分解終了。
①~④の式をつなげていくことで、
\frac{97}{99}=\frac{1}{2}+\frac{1}{3}+\frac{1}{7}+\frac{1}{278}+\frac{1}{96327}が得られる。
最後の例になると、本当に単位分数が出てくるのか不安になりますが、有限回の計算で必ず単位分数が登場するので、安心して(?)計算してください。
方法②:不等式でしぼっていく
もう一つの方法は、分解後の単位分数の個数を2個と固定したうえで、不等式から分母の数字をしぼっていく方法です。
こちらの方法では、分解後の式が何種類も出てきます。
実際の例を見てみましょう。
$~\displaystyle \frac{1}{4}~$の単位分数分解
① $~\displaystyle \frac{1}{4}=\frac{1}{x}+\frac{1}{y}~~~( x < y )~$とおく。
② $~x \le 4~$では、$~\displaystyle \frac{1}{x} \ge \frac{1}{4}~$のため、
\frac{1}{4}=\frac{1}{x}+\frac{1}{y}\ge \frac{1}{4}+\frac{1}{y}
となり、$~\displaystyle 0 \ge \frac{1}{y}~$は不適。
また、$~8 \le x~$では、$~\displaystyle \frac{1}{8} \ge \frac{1}{x}~$のため、
\frac{1}{4}=\frac{1}{x}+\frac{1}{y}\le \frac{1}{8}+\frac{1}{y}
となり、$~\displaystyle \frac{1}{x} \le \frac{1}{8} \le \frac{1}{y}~$は$~ x > y~$に不適。
よって、あてはまる$~x~$の条件は$~4 < x < 8~$となるため、$~x=5~,~6~,~7~$である。
③ それぞれの$~x~$を代入し、$~y~$を求めていく。
(ⅰ) $~x=5~$のとき、
\begin{align*}
\frac{1}{4}&=\frac{1}{5}+\frac{1}{y} \\
\\
\therefore~~~\frac{1}{4}&=\frac{1}{5}+\frac{1}{20} \\
\end{align*}より、単位分数分解終了。
(ⅱ) $~x=6~$のとき、
\begin{align*}
\frac{1}{4}&=\frac{1}{6}+\frac{1}{y} \\
\\
\therefore~~~\frac{1}{4}&=\frac{1}{6}+\frac{1}{12} \\
\end{align*}より、単位分数分解終了。
(ⅲ) $~x=7~$のとき、
\begin{align*}
\frac{1}{4}&=\frac{1}{7}+\frac{1}{y} \\
\\
\therefore~~~\frac{1}{4}&=\frac{1}{7}+\frac{3}{28} \\
\end{align*}なので、$~\displaystyle \frac{3}{28}~$の単位分数分解を行っていく。
① $~\displaystyle \frac{3}{28}=\frac{1}{a}+\frac{1}{b}~~~( a < b )~$とおく。
② $~a~$にあてはまる自然数は、$~9.33\cdots < a < 18.66\cdots~$より、$~a=10~,~11~,~12~,\cdots,~18~$である。
③ それぞれの$~a~$を代入し、$~b~$を求めていく。
(ⅰ) $~a=10~$のとき、
\begin{align*}
\frac{3}{28}&=\frac{1}{10}+\frac{1}{y} \\
\\
\therefore~~~\frac{3}{28}&=\frac{1}{10}+\frac{1}{140} \\
\end{align*}より単位分数分解終了で、もとの③(ⅲ)に代入すると、
\frac{1}{4}=\frac{1}{7}+\frac{1}{10}+\frac{1}{140}となる。
(ⅱ) $~a=11~$のとき、
\begin{align*}
\frac{3}{28}&=\frac{1}{11}+\frac{1}{y} \\
\\
\therefore~~~\frac{3}{28}&=\frac{1}{11}+\frac{5}{308} \\
\end{align*}より、$~\displaystyle \frac{5}{308}~$の単位分数分解を行っていく・・・。
‥‥以下略‥‥
このように場合分けが場合分けを生み、爆発的に分解パターンが増えていきます。
さらに言えば、(3)(ⅰ),(3)(ⅱ)の$~\displaystyle \frac{1}{5}~,~\frac{1}{20}~,~\frac{1}{6}~,~\frac{1}{12}~$についても、単位分数分解できるので、無限通り存在することが直感的にわかるでしょう。
すべての分数は無限通りに分解できる
単位分数分解の方法は理解できました。
例を挙げてきた通り、どんな分数でも単位分数分解できそうで、どんな分数でも無限通りの分解がありそうです。
これらについて証明していきます。
数学的帰納法で証明可能
ここで証明することを、命題の形でまとめます。
単位分数分解に関して、以下の2つの命題が成り立つ。
(1) すべての分数は単位分数分解できる。
(2) 単位分数分解の方法は無限通りある。
この2つの命題を、同時に証明していきます。
$~m~,~n~$を自然数として、分解したい任意の分数を$~\displaystyle \frac{n}{m}~$とおく。
分母$~m~$を固定し、$~\displaystyle \frac{n}{m}~$が異なる単位分数の和として表されることを数学的帰納法で示す。
$~n=1~$のときを考える。
$~\displaystyle \frac{1}{m}~$を式変形すると、
\begin{align*}
\frac{1}{m}&=\frac{m+1}{m(m+1)} \\
\\
&=\frac{m}{m(m+1)}+\frac{1}{m(m+1)} \\
\\
&=\frac{1}{m+1}+\frac{1}{m(m+1)}~~~~\cdots ①
\end{align*}となり、$~m > 1~$で$~m+1 < m(m+1)~$となるため、異なる単位分数の和として表される。
$~m=1~$のときについては、$①$より
\frac{1}{1}=\frac{1}{2}+\frac{1}{2}~~~~\cdots ②となってしまうが、$①$に$~m=2~$を代入すると、
\frac{1}{2}=\frac{1}{3}+\frac{1}{6}~~~~\cdots ③であり、$③$を$②$の2つめの$~\displaystyle \frac{1}{2}~$に代入することで、
\frac{1}{1}=\frac{1}{2}+\frac{1}{3}+\frac{1}{6}となり、異なる単位分数の和として表される。
以上より、$~n=1~$のとき、すなわち、すべての$~m~$について$~\displaystyle \frac{1}{m}~$が異なる単位分数の和として表されることが言えた。
$~n=k~$のとき、すなわち、$~\displaystyle \frac{k}{m}~$が異なる単位分数の和として表されることを仮定する。ここで、$~n=k+1~$のときを考える。
\frac{k+1}{m}=\frac{1}{m}+\frac{k}{m}より、$①$を代入することで、
\frac{k+1}{m}=\frac{1}{m+1}+\frac{1}{m(m+1)}+\frac{k}{m}~~~~\cdots④仮定より、$~\displaystyle \frac{k}{m}~$は異なる単位分数の和として表される。
その中に$~\displaystyle \frac{1}{m+1}~$や$~\displaystyle \frac{1}{m(m+1)}~$が含まれていなければ、$④$により$~n=k+1~$のときも異なる単位分数の和として表されることが言える。
しかし、$~\displaystyle \frac{k}{m}~$に例えば$~\displaystyle \frac{1}{m+1}~$が含まれている場合、すなわち
\frac{k}{m}=\frac{1}{m+1}+\frac{1}{a_1}+\cdots+\frac{1}{a_\ell} \\
~\\
(~a_1~,\cdots,a_\ell~は~m+1~以外のそれぞれ異なる自然数)と表され、この式を$④$に代入して、
\frac{k+1}{m}=\frac{1}{m+1}+\frac{1}{m(m+1)}+\frac{1}{m+1}+\frac{1}{a_1}+\cdots+\frac{1}{a_\ell}~~~~\cdots⑤となる。
ここで、$~\displaystyle \frac{1}{m+1}~$の重複を避けるべく、$①$の$~m~$に$~m+1~$を適用すると、
\begin{align*}
\frac{1}{m+1}&=\frac{1}{(m+1)+1}+\frac{1}{(m+1)(m+1+1)} \\
\\
&=\frac{1}{m+2}+\frac{1}{(m+1)(m+2)}~~~~\cdots ⑥
\end{align*}なので、$⑥$を$⑤$の2つ目の$~\displaystyle \frac{1}{m+1}~$に代入して、
\frac{k+1}{m}=\frac{1}{m+1}+\frac{1}{m(m+1)}+\frac{1}{m+2}+\frac{1}{(m+1)(m+2)}+\frac{1}{a_1}+\cdots+\frac{1}{a_\ell}~~~~\cdots⑦と表せる。
$⑦$の右辺に再度重複する単位分数があれば、$⑥$のような式を再度作って代入していくことで、いずれは異なる単位分数の和で右辺を表すことができる。
以上より、$~n=k+1~$のとき、すなわち、$~\displaystyle \frac{k+1}{m}~$が異なる単位分数の和として表されることが言えた。
したがって数学的帰納法より、命題(1)は示された。$~~~\blacksquare~$
また、異なる単位分数の和で表された後も、$⑥$のような式を作って、$⑦$のような式に代入していけば、単位分数をより細かくした式が無限に生成されるため、命題(2)も示されたことになる。$~~~\blacksquare~$
証明に具体例をあてはめてみた
証明が文字だらけでわかりにくかったので、分母が$~3~~(m=3)~$のときの単位分数分解を、この証明の流れを使って考えてみましょう。
$~\displaystyle \frac{n}{3}~$の単位分数分解($~m=3~$のとき)
$~n=1~$のときを考える。
$①$より、
\begin{align*}
\frac{1}{3}&=\frac{1}{3+1}+\frac{1}{3 \cdot (3+1)} \\
\\
&=\frac{1}{4}+\frac{1}{12}~\cdots ⑧
\end{align*}となるため、異なる単位分数の和として表された。
$~\displaystyle \frac{1}{3}~$が異なる単位分数の和として表されたので、$~\displaystyle \frac{2}{3}~$を考える。
\frac{2}{3}=\frac{1}{3}+\frac{1}{3}より、$⑧$を2つ目のの$~\displaystyle \frac{1}{3}~$に代入して、
\frac{2}{3}=\frac{1}{3}+\frac{1}{4}+\frac{1}{12}\cdots ⑨となるため、異なる単位分数の和として表された。
$~\displaystyle \frac{2}{3}~$が異なる単位分数の和として表されたので、$~\displaystyle \frac{3}{3}~$を考える。
\frac{3}{3}=\frac{1}{3}+\frac{2}{3}より、$⑨$を代入すると、
\frac{3}{3}=\frac{1}{3}+\frac{1}{3}+\frac{1}{4}+\frac{1}{12}となり、$~\displaystyle \frac{1}{3}~$が重複している。
そこで、2つめの$~\displaystyle \frac{1}{3}~$に$⑧$を代入すると、
\frac{3}{3}=\frac{1}{3}+\frac{1}{4}+\frac{1}{12}+\frac{1}{4}+\frac{1}{12}~\cdots ⑩であり、今度は$~\displaystyle \frac{1}{4}~$と$~\displaystyle \frac{1}{12}~$が重複している。
$①$の$~m~$に$~4~,~12~$をそれぞれ適用すると、
\begin{align*}
\frac{1}{4}&=\frac{1}{5}+\frac{1}{20} \\
\\
\frac{1}{12}&=\frac{1}{13}+\frac{1}{156}
\end{align*}なので、これらを$⑩$に代入すると、
\frac{3}{3}=\frac{1}{3}+\frac{1}{4}+\frac{1}{12}+\frac{1}{5}+\frac{1}{20}+\frac{1}{13}+\frac{1}{156}~~~\cdots ⑪となるため、異なる単位分数の和として表された。
これを$~n=4~,~n=5~,\cdots~$と繰り返していくのが、命題(1)の数学的帰納法による証明の内容である。
また、$①$の$~m~$に$~5~$を適用すると、
\frac{1}{5}=\frac{1}{6}+\frac{1}{30}なので、これを$⑪$に代入すると、
\frac{3}{3}=\frac{1}{3}+\frac{1}{4}+\frac{1}{12}+\frac{1}{6}+\frac{1}{30}+\frac{1}{20}+\frac{1}{13}+\frac{1}{156}となり、単位分数をより細かくした式が生成された。
これを無限に行えば、無限通りの分解できるというのが、命題(2)の証明の内容である。
具体的な数で考えると、証明で何をやっているかが中身がわかりやすかったですね。
あくまで証明としての考え方のため、実際に$~\displaystyle \frac{3}{3}~$を単位分数分解するなら、最大の単位分数を引いていく方法を使ったほうがわかりやすく、簡潔に表すことができます。
\frac{3}{3}=\frac{1}{2}+\frac{1}{3}+\frac{1}{6}まとめ
単位分数分解について解説してきました。
- 単位分数分解の方法は2通り。
- 単位分数分解はどんな分数でも必ずできる。
- 1つの分数を無限通りに単位分数分解できる。
3500年以上前のエジプトにおける、単位分数の表し方や使われ方についても、是非ご覧ください↓


単位分数分解の利点、わかったかな?



平等に分けられるという点は理解したものの、実際にパンを$~15~$等分するのは無理では?
ピザだとしても$~24^{\circ}~$‥‥。
◇参考文献等
・志賀浩二(2014)『数学の流れ30講(上)ー16世紀までー』,pp.20-24,朝倉書店.
・中村滋(2019)『ずかん 数字』,pp.48-49,技術評論社.

コメント
コメント一覧 (2件)
このサイトとても面白いので読み漁っていますがmathjax (たぶん) が変換されずにそのまま表示されています
aerobatさん
コメントありがとうございます。
サイトリニューアルした際に数式が崩れてしまい、依然直せていないページがある状況です。
できるだけ早急に修正したいと思います。
今後ともよろしくお願いします。
(ますひすもご覧いただきありがとうございます。)