わり算をするうえで、必要となってくるのが分数。
古代エジプトにおいても、「9個のパンを10人で分ける方法」が考えられました。
この問題に対して「1人あたり$~\displaystyle \frac{9}{10}~$個」ではなく、単位分数の和を使って「1人あたり$~\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{15}~$個」と、古代エジプトでは答えを出しています。
なぜ分子が$~1~$である単位分数を使っていたのでしょうか?
この記事では、古代エジプトの単位分数の表し方と使っていた理由について解説します。
- 古代エジプトの分数は、単位分数と$~\displaystyle \frac{2}{3}~$のみ。
- 分子が$~1~$ではない分数は、単位分数の和で表す。
- 古代エジプトが単位分数を使用した理由は、実用的だから。
| 時代 | B.C.1650年頃 |
| 場所 | エジプト |
古代エジプトの分数表記
古代エジプトでは、象形文字の一種であるヒエログリフやヒエラティックの数字が使われ、加減乗除も効率的に行われていました。

除法で割りきれないときに必要となる分数は、古代エジプトから存在し、独自の方法で表されています。
単位分数の表記方法は数字の上に口型の記号
古代エジプトの分数は、基本的に単位分数(分子が$~1~$の分数)のみしかありません。(理由は後述)
その表し方は簡単で、ヒエログリフであれば分母を表す数字の上に口型の記号を書くだけ。
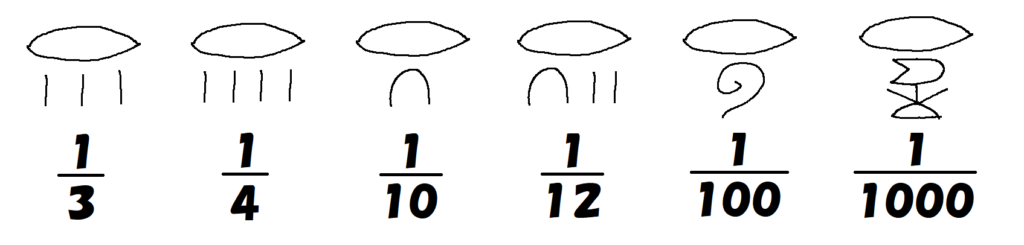
すなわち、古代エジプトで表すことのできる最小の数は$~\frac{1}{9999999}~$となります。

整数の表し方に関しては、以下の記事を参考にしてください。

特殊な分数は2種類
整数の上に口型の記号を書くだけという単純なルールで定義された分数でしたが、例外が2つありました。
それは$~\displaystyle \frac{1}{2}~$で、特殊な記号を用いて表します。

先ほどまでのルールに則れば、$~\displaystyle \frac{1}{2}~$は口型記号の下に縦棒2本で表せそうです。
しかし、その表記は$~\displaystyle \frac{2}{3}~$に割り当てられていました。

単位分数のみの中で$~\displaystyle \frac{2}{3}~$だけが特別に登場している理由は定かではないものの、「2倍法」が関係しているのではないかと考えられています。
ヒエラティックの分数は口型の記号の代わりに点
これまでに登場した分数は、すべてヒエログリフによるものですが、時代的に並行して発展したヒエラティックによる分数の表し方もあります。
こちらも単位分数と$\displaystyle ~\frac{2}{3}~$のみの取り扱いとなり、単位分数の表し方は、分母を表す数字の上に点を書くというもの。
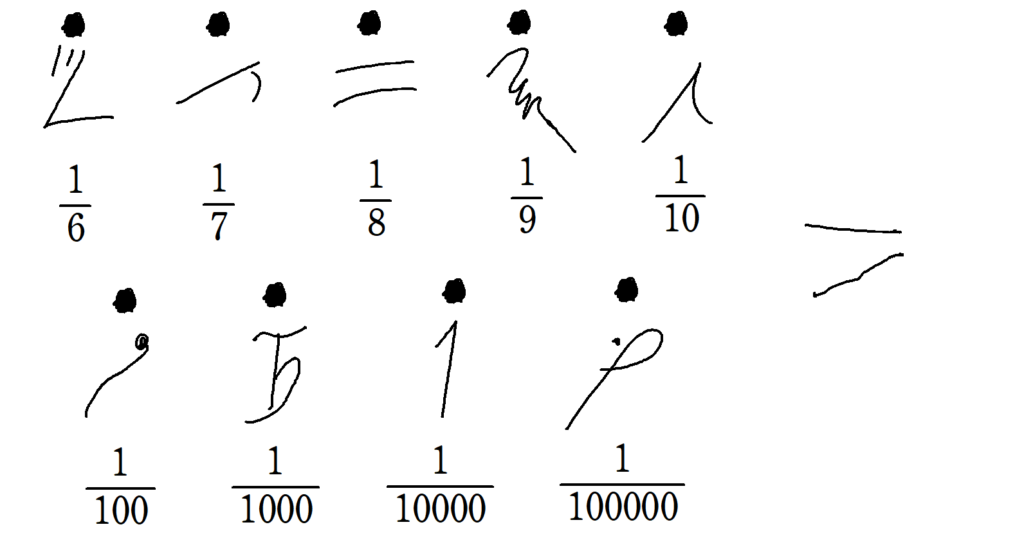
単位分数に加えて、$~\displaystyle \frac{2}{3}~$は専用の記号(図6)で表していました。

分子が 1 でない分数の表し方
単位分数と$~\displaystylle \frac{2}{3}~$のみが用意されていた古代エジプト。
$~\displaystyle \frac{2}{5}~$や$~\displaystyle \frac{3}{4}~$といった分数は、どう表現されたのでしょうか?
分子が 1 でない分数は単位分数の和で表す
単位分数以外は、直接数字で表すことができなかったため、単位分数の和で表されました。
$~\displaystyle \frac{2}{5}~$は次のように表せる。

それぞれ$~\displaystyle \frac{1}{3}~$と$~\displaystyle \frac{1}{15}~$を表す分数、つまり、
\begin{align*}
\frac{2}{5}=\frac{1}{3}+\frac{1}{15}
\end{align*}と単位分数に分解して、$~\displaystyle \frac{2}{5}~$を表していたことがわかります。
実際、すべての分数は単位分数の和として表すことができます。
『リンド・パピルス』に載っていた分数表
紀元前1650年頃に書かれたと推定される「リンド・パピルス」には、$~\displaystyle \frac{2}{n}~$($~n~$は$~5~$から$~101~$までの奇数)の単位分数分解の表が載っていました。

(出典:Paul James Cowie (Pjamescowie) / Public domain)
日常の計算の中でよく使われていたとされる$~\displaystyle \frac{2}{n}~$の分解が、次のように計49個載っていました。
\begin{align*}
\frac{2}{5}&=\frac{1}{3}+\frac{1}{15}\\
\\
\frac{2}{7}&=\frac{1}{4}+\frac{1}{28} \\
\\
\frac{2}{9}&=\frac{1}{6}+\frac{1}{18} \\
\\
\frac{2}{11}&=\frac{1}{6}+\frac{1}{66} \\
\\
\frac{2}{13}&=\frac{1}{8}+\frac{1}{52}+\frac{1}{104} \\
\\
\frac{2}{15}&=\frac{1}{10}+\frac{1}{30} \\
\\
\frac{2}{17}&=\frac{1}{12}+\frac{1}{51}+\frac{1}{68} \\
\\
\frac{2}{19}&=\frac{1}{12}+\frac{1}{76}+\frac{1}{114} \\
&~~~~~~~~~\vdots \\
&~~~~~~~~~\vdots \\
\\
\frac{2}{101}&=\frac{1}{101}+\frac{1}{202}+\frac{1}{303}+\frac{1}{606}
\end{align*}
ちなみに、単位分数に分解する方法は一通りではなく、
\frac{2}{5}=\frac{1}{4}+\frac{1}{7}+\frac{1}{140}などと表すこともできます。
『リンド・パピルス』に載っている分解方法が好まれた理由は、定かではありません。
古代エジプトで単位分数が使われた理由
すべての分数は、単位分数の和で表すことができます。

ただ、単位分数が古代エジプトで好まれた理由はどこにあったのでしょう?
その理由は、実生活の中にありました。
不平等なパンの分け方
『リンド・パピルス』の中には、以下のような問題があります。
$~9~$個のパンを$~10~$人で分ける方法は?
今の我々であれば、$~9 \div 10 =\displaystyle \frac{9}{10}~$という計算から、一人あたり$~\displaystyle \frac{9}{10}~$個のパンに分けられるという答えを出しますが、これは分け方として現実的ではありません(図9)。
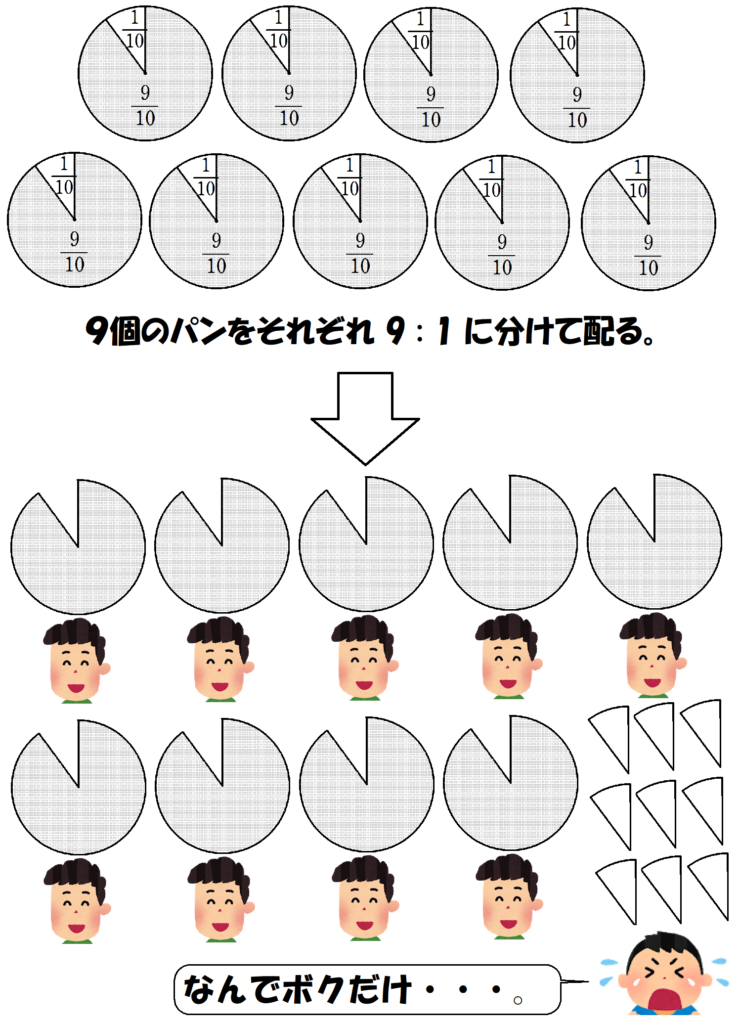
全員が$~\displaystyle \frac{9}{10}~$個のパンをもらっていることに変わりはないのですが、一人だけ他の9人のパンの余りをもらっています。さすがに不公平でしょう。
単位分数を使うとパンが平等に分けられる
『リンド・パピルス』に載っている、この問題の解決方法が単位分数分解なのです。
「単位分数分解(方法編)」にならって、$~\displaystyle \frac{9}{10}~$をエジプトの分数表記にしてみましょう。
$~\displaystyle \frac{9}{10}~$から一番大きな単位分数をとることで、
\frac{9}{10}=\frac{1}{2}+\frac{2}{5}~~~~\cdots ①であり、次に$~\displaystyle \frac{2}{5}~$を『リンド・パピルス』の単位分数分解表(抜粋)に従って分解すると、
\frac{2}{5}=\frac{1}{3}+\frac{1}{15}~~~~\cdots ②となる。
よって、$②$を$①$に代入して、
\frac{9}{10}=\frac{1}{2}+\frac{1}{3}+\frac{1}{15}が成り立つ。
この計算から、一人あたり$~\displaystyle \frac{9}{10}~$のパンを得るためには、$~\displaystyle \frac{1}{2}~$のパンと$~\displaystyle \frac{1}{3}~$のパンと$~\displaystyle \frac{1}{15}~$のパンを組み合わせればいいことがわかります。
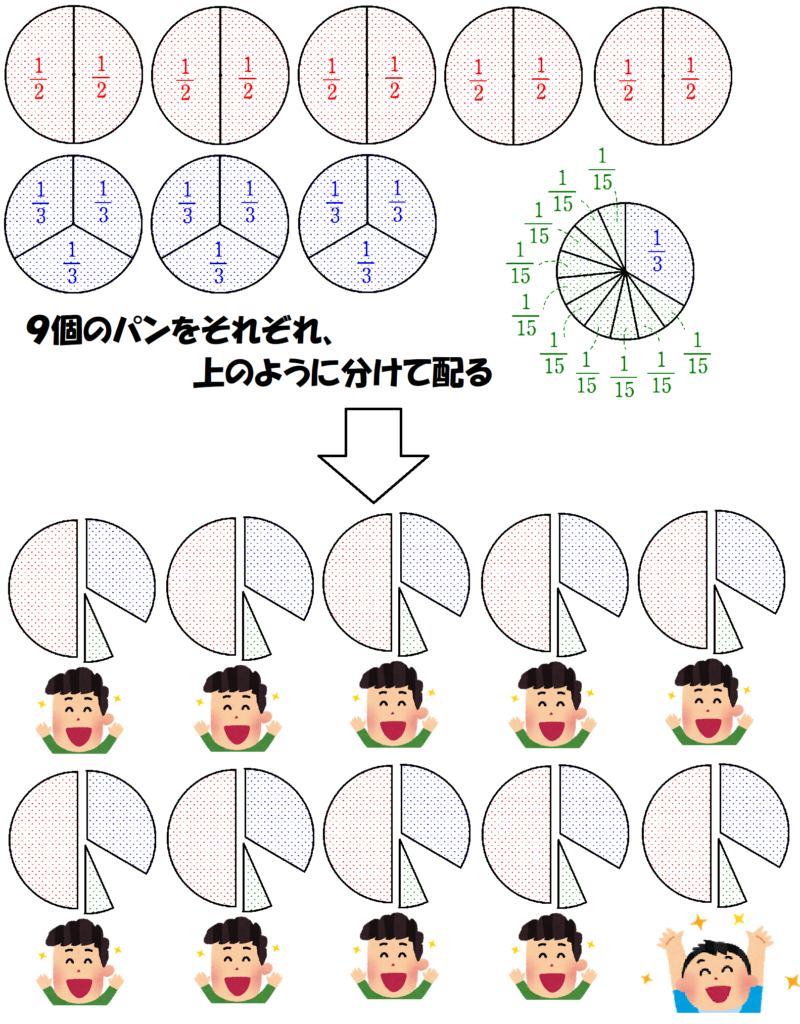
単位分数分解により、形まで平等に分けることができました。
この「分けやすい」という実用的な点に単位分数の強みがあるのです。
まとめ・参考文献
古代エジプトの分数について解説してきました。
- 古代エジプトの分数は、単位分数と$~\displaystyle \frac{2}{3}~$のみ。
- 分子が$~1~$ではない分数は、単位分数の和で表す。(『リンド・パピルス』に分数表あり)
- 古代エジプトが単位分数を使用した理由は、”分ける”という点で実用的だから。
古代エジプトでは、パンの分け方からもわかるよう、実用的な計算を重視しました。
しかし、この実用的な側面を重視したがために生じた計算の不便さは、エジプト数学の発展の妨げともなっていました。
次の記事では、『リンド・パピルス』や『モスクワ・パピルス』に載っている問題から、古代エジプトの数学レベルを見てみましょう。



単位分数分解、面倒だけど確かに実用的!



でも、計算上は超不便だよ。『リンド・パピルス』には、
「$~\displaystyle \frac{1}{16}+\frac{1}{112}~$と$~\displaystyle 1+\frac{1}{2}+\frac{1}{4}~$の積を求めなさい」という問題があるんだけど、普通の分数が使えれば、$~\displaystyle \frac{1}{14}~$と$~\displaystyle \frac{7}{4}~$の積だから、簡単に求まるよね。
参考文献(本の紹介ページにリンクしています)
- 『カッツ 数学の歴史』,pp.13-15
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,pp.10-13
- 『数学史 数学5000年の歩み』,pp.21-25
- 『数学の流れ30講(上)』,pp.20-24
- 『ずかん 数字』,pp.44-49

コメント