東京都私学教員適性検査の過去問(平成31年度)の答えを解説付きで載せています。
問題集の解答例で、解法を調べたい際にご活用ください。
大問1(本ページ)
大問2
※大問3~5に関しては、問題集の解答の中に解法まで載っています。
他の年度については、コチラからどうぞ。
サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
解説の内容自体に影響はありません。
問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。
1
(1) $~6\sqrt{3}~$
(2) $~0 < a < 1~$
(3) $~\displaystyle \frac{90}{7}~$
(4) $~6~$
(5) 平均 $~1~$ 本、相関係数 $~\displaystyle \frac{3\sqrt{2}}{8}~$
(6) $~11~$
(7) $~-1~$
(8) $~2 \cos{2x}~$
(9) $~\displaystyle \frac{e^x}{2}(\sin{x}+\cos{x})+C~$
(10) $~z=-4~$
1(1)
まず、 $~xy~$ を求める。 $~x+y=\sqrt{3}~$ の両辺を2乗し、 $~x^2+y^2=5~$ を代入すると、
\begin{align}
(x+y)^2&=3 \\
x^2+y^2+2xy&=3 \\
5+2xy&=3 \\
2xy&=-2 \\
xy&=-1
\end{align}
となる。
$~x^3+y^3~$ の因数分解の公式から、
\begin{align}
x^3+y^3&=(x+y)(x^2-xy+y^2) \\
&=\sqrt{3}\cdot \{5-(-1)\} \\
&=6\sqrt{3}
\end{align}
が求まった。
1(2)
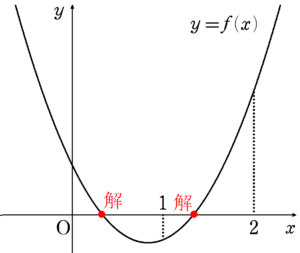
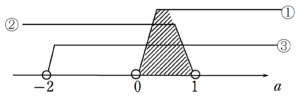
$~f(x)=2x^2-3x+a~$ とし、 $~y=f(x)~$ のグラフの形を考えると、次のようになる。
このとき、満たすべき条件は、
\begin{cases}
f(0) > 0 & \cdots① \\
f(1) < 0 & \cdots② \\
f(2) > 0 & \cdots③ \\
\end{cases}
の3つである。
①より、
\begin{equation}
a > 0
\end{equation}
②より、
\begin{align}
2\cdot 1^2-3\cdot 1+a &< 0 \\
2-3+a &< 0 \\
a &< 1
\end{align}
③より、
\begin{align}
2\cdot 2^2-3\cdot 2 +a &> 0 \\
8-6+a &> 0 \\
a &> -2
\end{align}
以上より、
となるため、 $~0 < a < 1~$ が求まった。
1(3)
各分数の分母・分子をそれぞれ素因数分解して表すと、
\begin{align}
\displaystyle \frac{42}{5}&=\frac{2 \cdot 3 \cdot 7}{5} \\
\\
\frac{21}{10}&=\frac{3 \cdot 7}{5 \cdot 2} \\
\\
\frac{35}{18}&=\frac{5 \cdot 7}{2 \cdot 3^2} \\
\end{align}
となり、いずれにかけても積が自然数となるためには、求めるべき分数の分子は、3つの分数の分母の公倍数となる必要がある。
しかも、最も小さいものを求めたいため、最小公倍数をもとめればよい。したがって、
\begin{equation}
(分子)=2 \cdot 3^2 \cdot 5 =90
\end{equation}
と求まる。
また、求めるべき分数の分母は、3つの分数の分子とそれぞれ約分ができないといけないので、分子の公約数となる必要がある。
しかも、求める分数自体を最小にするには、分母が最大のものを求めたいため、最大公約数を求めればよい。したがって、
\begin{equation}
(分母)=7
\end{equation}
と求まる。
以上より、求めたい分数は $~\displaystyle \frac{90}{7}~$ と求まった。
1(4)
$~5~$ の累乗の中で、 $~19~$ で割ったときの余りが $~1~$ となるものを探す。
\begin{align}
5^1&=5 \equiv 5 \pmod{19} \\
5^2&=25 \equiv 6 \pmod{19} \\
5^3&\equiv 5 \cdot 6=30 \equiv 11 \pmod{19} \\
5^4&\equiv 6^2=36 \equiv 17 \pmod{19} \\
5^5&\equiv 6 \cdot 11=66 \equiv 9 \pmod{19} \\
5^6&\equiv 11^2=121 \equiv 7 \pmod{19} \\
5^7&\equiv 5 \cdot 7=35 \equiv 16 \pmod{19} \\
5^8&\equiv 6 \cdot 7=42 \equiv 4 \pmod{19} \\
5^9&\equiv 5 \cdot 4=20 \equiv 1 \pmod{19} \\
\end{align}
これにより、
\begin{align}
5^2000&=(5^9)^222 \cdot 5^2 \\
&\equiv 1^222 \cdot 25 \pmod(19) \\
&=25 \\
&\equiv 6 \pmod(19)
\end{align}
となるので、余りは $~6~$ と求まった。
1(5)
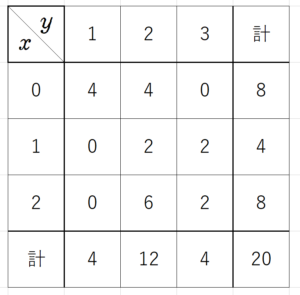
まず、表に「合計」を加えたものを作る。
これにより、シャーペンの本数の平均 $~\mu_{x}~$ は、
\begin{align}
\displaystyle \mu_{x}&=\frac{0 \cdot 8+1 \cdot 4+2 \cdot 8}{20} \\
\\
&=\frac{20}{20} \\
\\
&=1
\end{align}
と求まった。
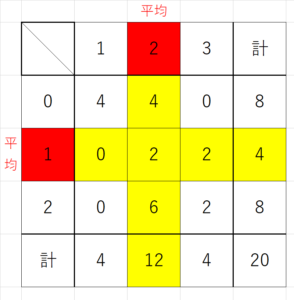
また、同様の計算でボールペンの本数の平均 $~\mu_{y}=2~$ が求まるため、次に $~x~$ の分散、 $~y~$ の分散、 $~x,y~$ 共分散をそれぞれ求める。
ここで、下の表中で黄色で塗られたデータに関しては、 $~(x-\mu_{x}=0~$ または $~(y-\mu_{y}=0~$ となることを利用すれば、
$~x~$ の分散 $~\sigma_{x}~$ は、
\begin{align}
\sigma_{x}&=\displaystyle \frac{1}{20} \left\{ 8 \cdot (0-1)^2+8 \cdot (2-1)^2 \right\} \\
\\
&=\frac{1}{20} (8+8) \\
\\
&=\frac{16}{20}
\end{align}
であり、 $~y~$ の分散 $~\sigma_{y}~$ は、
\begin{align}
\sigma_{y}&=\displaystyle \frac{1}{20} \left\{ 4 \cdot (1-2)^2+4 \cdot (3-2)^2 \right\} \\
\\
&=\frac{1}{20} (4+4) \\
\\
&=\frac{8}{20}
\end{align}
であり、 $~x,y~$ の共分散 $~\sigma_{xy}~$ は
\begin{align}
\sigma_{xy}&=\displaystyle \frac{1}{20} \left\{ 4 \cdot (0-1)(1-2)+2(2-1)(3-2) \right\} \\
\\
&=\frac{1}{20} (4+2) \\
\\
&=\frac{6}{20}
\end{align}
となる。
以上3つの数値より、相関係数は
\begin{align}
\displaystyle \frac{\sigma_{xy}}{\sqrt{\sigma_{x}}\sqrt{\sigma_{y}}}&=\frac{\frac{6}{20}}{\sqrt{\frac{16}{20}}\sqrt{\frac{8}{20}}} \\
\\
&=\frac{6}{\sqrt{16}\sqrt{8}} \\
\\
&=\frac{6}{4\cdot 2\sqrt{2}} \\
\\
&=\frac{6\sqrt{2}}{16} \\
\\
&=\frac{3\sqrt{2}}{8}
\end{align}
が求まった。
1(6)
左辺と右辺をそれぞれ、底が $~2~$ の対数にまとめるべく式変形をしていく。
\begin{align}
\displaystyle \log_{2}{(n-1)}-\log_{\frac{1}{2}}{(n+5)} &\le 4+\log_{2}{n} \\
\\
\log_{2}{(n-1)}-\log_{2^{-1}}{(n+5)} &\le 4 \log_{2}{2}+\log_{2}{n} \\
\\
\log_{2}{(n-1)}+\log_{2}{(n+5)} &\le \log_{2}{2^4}+\log_{2}{n} \\
\\
\log_{2}{(n-1)(n+5)} &\le \log_{2}{(16n)}
\end{align}
底が $~1~$ より大きいため、対数の大小は、真数の大小と同値なので、
\begin{align}
(n-1)(n+5) &\le 16n \\
n^2+4n-5 &\le 16n \\
n^2-12n-5 &\le 0
\end{align}
となり、この二次不等式の解は
\begin{equation}
6-\sqrt{41} \le n \le 6+\sqrt{41}
\end{equation}
である。すなわち、 $~6 < \sqrt{41} < 7~$ から、
\begin{equation}
n=0,1,2,3,4,5,6,7,8,9,10,11,12 \cdots ①
\end{equation}
が求まる。
また、元の不等式の真数条件から、
\begin{cases}
n-1 > 0 & \Longrightarrow n > 1 \\
n+5 > 0 & \Longrightarrow n > -5 \\
n > 0 &
\end{cases}
となるので、まとめると、
\begin{equation}
n > 1 \cdots ②
\end{equation}
である。
①、②より、
\begin{equation}
n=2,3,4,5,6,7,8,9,10,11,12
\end{equation}
が解となるため、 $~11~$ 個であることが求まった。
1(7)
$~x=-t~$ と置換し、式変形していくと、
\begin{align}
&\displaystyle \lim_{x \to -\infty}{(\sqrt{x^2+x+1}-\sqrt{x^2-x+1})} \\
\\
&=\lim_{t \to \infty}{(\sqrt{t^2-t+1}-\sqrt{t^2+t+1})} \\
\\
&=\lim_{t \to \infty}{\frac{(\sqrt{t^2-t+1}-\sqrt{t^2+t+1})(\sqrt{t^2-t+1}+\sqrt{t^2+t+1})}{(\sqrt{t^2-t+1}+\sqrt{t^2+t+1})}} \\
\\
&=\lim_{t \to \infty}{\frac{(t^2-t+1)-(t^2+t+1)}{\sqrt{t^2-t+1}+\sqrt{t^2+t+1}}} \\
\\
&=\lim_{t \to \infty}{\frac{-2t}{\sqrt{t^2-t+1}+\sqrt{t^2+t+1}}} \\
\\
&=\lim_{t \to \infty}{\frac{-2}{\sqrt{1-\frac{1}{t}+\frac{1}{t^2}}+\sqrt{1+\frac{1}{t}+\frac{1}{t^2}}}} \\
\\
&=\frac{-2}{\sqrt{1-0+0}+\sqrt{1+0+0}} \\
\\
&=\frac{-2}{2} \\
\\
&=-1
\end{align}
\begin{align}
&\displaystyle \lim_{x \to -\infty}{(\sqrt{x^2+x+1}-\sqrt{x^2-x+1})} \\
\\
&=\lim_{t \to \infty}{(\sqrt{t^2-t+1}-\sqrt{t^2+t+1})} \\
\end{align}
であり、ここで分母・分子に $~(\sqrt{t^2-t+1}+\sqrt{t^2+t+1})~$ をかけると、
\begin{align}
&=\lim_{t \to \infty}{\frac{(t^2-t+1)-(t^2+t+1)}{\sqrt{t^2-t+1}+\sqrt{t^2+t+1}}} \\
\\
&=\lim_{t \to \infty}{\frac{-2t}{\sqrt{t^2-t+1}+\sqrt{t^2+t+1}}} \\
\\
&=\lim_{t \to \infty}{\frac{-2}{\sqrt{1-\frac{1}{t}+\frac{1}{t^2}}+\sqrt{1+\frac{1}{t}+\frac{1}{t^2}}}} \\
\\
&=\frac{-2}{\sqrt{1-0+0}+\sqrt{1+0+0}} \\
\\
&=\frac{-2}{2} \\
\\
&=-1
\end{align}
が求まった。
※ $~x \to -\infty~$ のまま計算をしてしまうと、 $~\sqrt{\quad}~$ の部分で絶対値の関係から、符号を考えてあげないといけなくなるため、ミスしやすいです。
1(8)
与式である
\begin{equation}
f(x)=\displaystyle \int_{\pi}^{2x}\cos{t}dt
\end{equation}
を微分すると、微分と積分の関係から、
\begin{align}
f'(x)&=\cos{2x}\cdot (2x)’ \\
&=2\cos{2x}
\end{align}
が求まった。
※不安な人は、右辺の積分計算してから微分すると確実に正答できます↓↓
\begin{align}
f(x)&=\displaystyle \left[ \sin{t} \right]_{\pi}^{2x} \\
\\
&=\sin{2x}-\sin{\pi} \\
\\
&=\sin{2x}
\end{align}
なので、この式を微分すればよい。
1(9)
同じ積分の式が出てくるまで、部分積分を繰り返すと、
\begin{align}
\displaystyle &\int e^x \cos{x}dx \\
\\
&=\int (e^x)’ \cos{x}dx \\
\\
&=e^x \cos{x}+\int e^x \sin{x}dx \\
\\
&=e^x \cos{x}+\int (e^x)’ \sin{x}dx \\
\\
&=e^x \cos{x}+e^x \sin{x}-\int e^x \cos{x}dx \\
\\
&=e^x (\cos{x}+\sin{x})-\int e^x \cos{x}dx \\
\end{align}
となる。(途中の積分定数は省略している。)
したがって、
\begin{align}
\displaystyle 2\int e^x \cos{x}dx &=e^x (\cos{x}+\sin{x}) \\
\\
\int e^x \cos{x}dx &=\frac{e^x}{2} (\cos{x}+\sin{x}) \\
\end{align}
であり、積分定数 $~C~$ を加え、
\begin{equation}
\displaystyle \int e^x \cos{x}dx =\frac{e^x}{2} (\cos{x}+\sin{x})+C
\end{equation}
が求まった。
1(10)
$~A,B,C,D~$ が同じ平面上にあるとき、
\begin{equation}
\overrightarrow{AD}=s\overrightarrow{AB}+t\overrightarrow{AC}
\end{equation}
で表せる。
\begin{equation}
\overrightarrow{AB} = \left(
\begin{array}{c}
-1 \\
1 \\
0
\end{array}
\right),
\overrightarrow{AC} = \left(
\begin{array}{c}
-1 \\
0 \\
1
\end{array}
\right),
\overrightarrow{AD} = \left(
\begin{array}{c}
6 \\
-2 \\
z
\end{array}
\right)
\end{equation}
\begin{equation}
\overrightarrow{AB} = \left(
\begin{array}{c}
-1 \\
1 \\
0
\end{array}
\right),
\overrightarrow{AC} = \left(
\begin{array}{c}
-1 \\
0 \\
1
\end{array}
\right),\\
\\
\overrightarrow{AD} = \left(
\begin{array}{c}
6 \\
-2 \\
z
\end{array}
\right)
\end{equation}
なので、
\begin{align}
\left(
\begin{array}{c}
6 \\
-2 \\
z
\end{array}
\right)&=s \left(
\begin{array}{c}
-1 \\
1 \\
0
\end{array}
\right)+t \left(
\begin{array}{c}
-1 \\
0 \\
1
\end{array}
\right) \\
\\
\left(
\begin{array}{c}
6 \\
-2 \\
z
\end{array}
\right)&=\left(
\begin{array}{c}
-s \\
s \\
0
\end{array}
\right)+ \left(
\begin{array}{c}
-t \\
0 \\
t
\end{array}
\right) \\
\end{align}
であるため、各成分に注目すると、
\begin{cases}
6&=-s-t \cdots ① \\
-2&=s \cdots ② \\
z&=t \cdots ③
\end{cases}
である。
②に①を代入して、
\begin{align}
6&=-(-2)-t \\
t&=-4
\end{align}
となり、これを③に代入すると、
\begin{equation}
z=t=-4
\end{equation}
が求まった。
※ちなみに、平面の方程式が $~x+y+z=1~$ と簡単に求まるため、ここに $~D~$ の座標を代入すれば、すぐに $~z~$ が求まります。。
(3),(4)あたりは少しクセの強さを感じましたが、あとは一般的な問題ばかりでした。

◇参考文献等
・『私学教員適性検査問題集 数学(平成29年度~31年度)』

コメント