東京都私学教員適性検査の過去問(令和2年度)の答えを解説付きで載せています。
問題集の解答例で、解法を調べたい際にご活用ください。
大問1(本ページ)
大問2
※大問3~5に関しては、問題集の解答の中に解法まで載っています。
他の年度については、コチラからどうぞ。
サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
解説の内容自体に影響はありません。
問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。
1
(1) $~2~$
(2) $~y=9x-14~,~y=4~$
(3) $~\sin{x}~$
(4) $~\displaystyle \frac{5}{46}~$
(5) $~a=48~,~b=84~$
(6) $~\bar{x’}=4\bar{x}+7~,~s_{x’}=4s_x~,~S’=36S~$
(7) $~5 \sqrt{2}~$
(8) $~\displaystyle \frac{1}{2}x \left| \sin{(\log{x})}-\cos{(\log{x})} \right|+C~$
1(1)
\begin{align}
&~~~(与式) \\
&=\log_{10}{2^3}+\log_{10}{(10^2 \cdot 2^2)}-5\log_{10}{2} \\
&=3\log_{10}{2}+\log_{10}{10^2}+\log_{10}{2^2}-5\log_{10}{2} \\
&=3\log_{10}{2}+2+2\log_{10}{2}-5\log_{10}{2} \\
&=2
\end{align}
1(2)
$~y’=3x^2-3~$より、曲線上の点$~(~t~,~t^3-3t+2~)~$における接線の方程式を考えると、
\begin{align}
y-(t^3-3t+2)&=(3t^2-3)(x-t) \\
y-t^3+3t-2&=(3t^2-3)x-3t^3+3t \\
y&=(3t^2-3)x-2t^3+2 ~~~\cdots (*)
\end{align}
この接線が、点$~(~2~,~4~)~$を通るため、
\begin{align}
4&=(3t^2-3)\cdot 2-2t^3+2 \\
4&=6t^2-6-2t^3+2 \\
4&=-2t^3+6t^2-4
\end{align}
この方程式を解くことで、
\begin{align}
2t^3-6t^2+8&=0 \\
t^3-3t^2+4&=0 \\
(t+1)(t^2-4t+4)&=0 \\
(t+1)(t-2)^2&=0 \\
t&=-1~,~2
\end{align}
が求まる。
$~t=-1~$を$(*)$に代入することで、
\begin{align}
y&=\{3\cdot (-1)^2-3\}x-2\cdot (-1)^3+2 \\
y&=0+2+2 \\
y&=4
\end{align}
が求まり、$~t=2~$を$(*)$に代入することで、
\begin{align}
y&=(3\cdot 2^2-3)x-2\cdot 2^3+2 \\
y&=9x-16+2 \\
y&=9x-14
\end{align}
が求まる。
1(3)
三角関数の加法定理を利用する。
\begin{align}
&~~~(与式) \\
\\
&=\displaystyle \sin{\frac{\pi}{3}}\cos{x}+\cos{\frac{\pi}{3}} \sin{x}-\left(\sin{\frac{\pi}{3}} \cos{x}-\cos{\frac{\pi}{3}} \sin{x} \right) \\
\\
&=\displaystyle \sin{\frac{\pi}{3}}\cos{x}+\cos{\frac{\pi}{3}} \sin{x}-\sin{\frac{\pi}{3}} \cos{x}+\cos{\frac{\pi}{3}} \sin{x} \\
\\
&=2\cos{\frac{\pi}{3}} \sin{x} \\
\\
&=2 \cdot \frac{1}{2} \cdot \sin{x} \\
\\
&=\sin{x}
\end{align}
\begin{align}
&~~~(与式) \\
\\
&=\displaystyle \sin{\frac{\pi}{3}}\cos{x}+\cos{\frac{\pi}{3}} \sin{x} \\
&~~~~~~~~~~~~~~~~~~~~-\left(\sin{\frac{\pi}{3}} \cos{x}-\cos{\frac{\pi}{3}} \sin{x} \right) \\
\\
&=\displaystyle \sin{\frac{\pi}{3}}\cos{x}+\cos{\frac{\pi}{3}} \sin{x}-\sin{\frac{\pi}{3}} \cos{x}+\cos{\frac{\pi}{3}} \sin{x} \\
\\
&=2\cos{\frac{\pi}{3}} \sin{x} \\
\\
&=2 \cdot \frac{1}{2} \cdot \sin{x} \\
\\
&=\sin{x}
\end{align}
1(4)
求めたい数列を次のようにおく。
\begin{equation}
\frac{1}{10}~,~a_{2}~,~a_{3}~,~a_{4}~,~a_{5}~,~\frac{1}{8}
\end{equation}
この数列の逆数は、次のように表せる。
\begin{equation}
10~,~\frac{1}{a_{2}}~,~\frac{1}{a_{3}}~,~\frac{1}{a_{4}}~,~\frac{1}{a_{5}}~,~8
\end{equation}
これが等差数列となるので、初項は$~10~$、第6項目は$~8~$より、公差を$~d~$とすると、
\begin{align}
8=10+(6-1)d \\
-2&=5d \\
d&=-\frac{2}{5}
\end{align}
とわかる。よって、
\begin{align}
\frac{1}{a_3}&=10+(3-1)\cdot \left( -\frac{2}{5} \right) \\
\\
&=10-\frac{4}{5} \\
\\
&=\frac{46}{5}
\end{align}
なので、$~a_{3}=\displaystyle \frac{5}{46}~$が求まった。
1(5)
最大公約数を $~d~$とする。
このとき、$~a=a’d~,~b=b’d~~$($~a’~,~b’~$は互いに素)と表せる。
$~a~$と$~b~$の和が$~132~$なので、
\begin{align}
a+b&=132 \\
a’d+b’d&=2^2\cdot 3 \cdot 11 \\
(a’+b’)d&=2^2\cdot 3 \cdot 11 ~~~~\cdots ①
\end{align}
また、$~a~$と$~b~$の最小公倍数が$~336~$なので、
\begin{align}
a’b’d&=336 \\
a’b’d&=2^4\cdot 3 \cdot 7 ~~~~\cdots ②
\end{align}
$~①~,~②~$より、$~d=2^2 \cdot 3=12~$と求まり、
$~①~$に代入することで、$~a’+b’=11~$、$~②~$に代入することで、$~a’b’=28~$とわかる。
解と係数の関係から、$~t=~a’~,~b’~$を求める方程式は、
\begin{align}
t^2-11t+28&=0 \\
(t-4)(t-7)&=0 \\
t&=~4~,~7~
\end{align}
よって、$~a’=4~,~b’=7~$なので、$~a=48~,~b=84~$が求まった。
1(6)
平均値
\begin{align}
\bar{x’}&=\frac{x’_1+\cdots+x’_n}{n} \\
\\
&=\frac{(4x_1+7)+\cdots+(4x_n+7)}{n} \\
\\
&=\frac{4(x_1+\cdots+x_n)+7n}{n} \\
\\
&=4 \cdot \frac{x_1+\cdots+x_n}{n}+7 \\
\\
&=4\bar{x}+7
\end{align}
標準偏差
まずは$~x’~$の分散を求める。
\begin{align}
s^2_{x’}&=\frac{(x’_1-\bar{x’})^2+\cdots+(x’_n-\bar{x’})^2}{n} \\
\\
&=\frac{\{(4x_1+7)-(4\bar{x}+7)\}^2+\cdots+\{(4x_n+7)-(4\bar{x}+7)\}^2}{n} \\
\\
&=\frac{(4x_1-4\bar{x})^2+\cdots+(4x_n-4\bar{x})^2}{n} \\
\\
&=\frac{4^2(x_1-\bar{x})^2+\cdots+4^2(x_n-\bar{x})^2}{n} \\
\\
&=16 \cdot \frac{(x_1-\bar{x})^2+\cdots+(x_n-\bar{x})^2}{n} \\
\\
&=16s^2_x
\end{align}
\begin{align}
s^2_{x’}&=\frac{1}{n}\left\{ (x’_1-\bar{x’})^2+\cdots+(x’_n-\bar{x’})^2 \right\} \\
\\
&=\frac{1}{n} \left[ \{(4x_1+7)-(4\bar{x}+7)\}^2+\cdots \right. \\
& \left. ~~~~~~~~~~~~~~~~~~~~+\{(4x_n+7)-(4\bar{x}+7)\}^2 \right] \\
\\
&=\frac{(4x_1-4\bar{x})^2+\cdots+(4x_n-4\bar{x})^2}{n} \\
\\
&=\frac{4^2(x_1-\bar{x})^2+\cdots+4^2(x_n-\bar{x})^2}{n} \\
\\
&=16 \cdot \frac{(x_1-\bar{x})^2+\cdots+(x_n-\bar{x})^2}{n} \\
\\
&=16s^2_x
\end{align}
この両辺の平方根をとることで、$~s_{x’}=4s_x~$が求まる。
共分散
\begin{align}
S’&=\frac{1}{n}\left[\{(4x_1+7)-(4\bar{x}+7)\}\{(9y_1+11)-(9\bar{y}+11)\}+\cdots \right. \\
& \left. ~~~~~~~+\{(4x_n+7)-(4\bar{x}+7)\}\{(9y_n+11)-(9\bar{y}+11)\} \right] \\
\\
&=\frac{ (4x_1-4\bar{x})(9y_1-9\bar{y})+\cdots+(4x_n-4\bar{x})(9y_n-9\bar{y})}{n} \\
\\
&=\frac{4(x_1-\bar{x})\cdot 9(y_1-\bar{y})+\cdots+4(x_n-\bar{x})\cdot 9(y_n-\bar{y})}{n} \\
\\
&=36\cdot \frac{(x_1-\bar{x})(y_1-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y})}{n} \\
\\
&=36S \\
\end{align}
\begin{align}
S’&=\frac{1}{n}\left[\{(4x_1+7)-(4\bar{x}+7)\}\{(9y_1+11)-(9\bar{y}+11)\} \right. \\
& \left.~ +\cdots \right. \\
& \left. ~~+\{(4x_n+7)-(4\bar{x}+7)\}\{(9y_n+11)-(9\bar{y}+11)\} \right] \\
\\
&=\frac{1}{n} \left\{ (4x_1-4\bar{x})(9y_1-9\bar{y})+\cdots \right. \\
& \left.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+(4x_n-4\bar{x})(9y_n-9\bar{y}) \right\} \\
\\
&=\frac{4(x_1-\bar{x})\cdot 9(y_1-\bar{y})+\cdots+4(x_n-\bar{x})\cdot 9(y_n-\bar{y})}{n} \\
\\
&=36\cdot \frac{(x_1-\bar{x})(y_1-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y})}{n} \\
\\
&=36S \\
\end{align}
1(7)
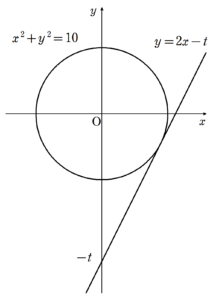
$~2x-y=t~$とする。
変形すると、$~y=2x-t~$なので、$~x^2+y^2=10~$との交点を考えると、次の図のように接するとき、$~t~$は最大となる。
直線の方程式を円の方程式に代入して、
\begin{align}
x^2+(2x-t)^2&=10 \\
x^2+4x^2-4tx+t^2-10&=0 \\
5x^2-4tx+t^2-10&=0 \\
\end{align}
となる。
これが解を1つだけ持つので、$~\displaystyle \frac{D}{4}~$を考えると、
\begin{align}
(-2t)^2-5(t^2-10)&=0 \\
4t^2-5t^2+50&=0 \\
-t^2&=-50 \\
t^2&=50 \\
t&=\pm 5\sqrt{2}
\end{align}
となり、$~t~$の最大値を求めたいので、$~t=5\sqrt{2}~$が求まった。
1(8)
部分積分法を2回使って変形する。
\begin{align}
&~~~\int \sin{(\log{x})}dx \\
&=\int (x)’\cdot \sin{(\log{x})}dx \\
&=x\sin{(\log{x})}-\int x \cos{(\log{x})}\cdot \frac{1}{x} dx \\
&=x\sin{(\log{x})}-\int \cos{(\log{x})} dx \\
&=x\sin{(\log{x})}-\int (x)’ \cdot \cos{(\log{x})} dx \\
&=x\sin{(\log{x})}-\left[ x\cos{(\log{x})} -\int x \cdot \{ -\sin{(\log{x})} \} \cdot \frac{1}{x} dx \right] \\
&=x\sin{(\log{x})}-x\cos{(\log{x})} -\int \sin{(\log{x})} dx \\
&=x\left\{ \sin{(\log{x})}-\cos{(\log{x})} \right\} -\int \sin{(\log{x})} dx \\
\end{align}
\begin{align}
&~~~\int \sin{(\log{x})}dx \\
&=\int (x)’\cdot \sin{(\log{x})}dx \\
&=x\sin{(\log{x})}-\int x \cos{(\log{x})}\cdot \frac{1}{x} dx \\
&=x\sin{(\log{x})}-\int \cos{(\log{x})} dx \\
&=x\sin{(\log{x})}-\int (x)’ \cdot \cos{(\log{x})} dx \\
&=x\sin{(\log{x})} \\
&~~~~~~~~~~~~-\left[ x\cos{(\log{x})} -\int x \cdot \{ -\sin{(\log{x})} \} \cdot \frac{1}{x} dx \right] \\
&=x\sin{(\log{x})}-x\cos{(\log{x})} -\int \sin{(\log{x})} dx \\
&=x\left\{ \sin{(\log{x})}-\cos{(\log{x})} \right\} -\int \sin{(\log{x})} dx \\
\end{align}
ここで、右辺の$~\displaystyle -\int \sin{(\log{x})}dx~$を左辺に移項することで、
\begin{align}
2\int \sin{(\log{x})} dx&=x\left\{ \sin{(\log{x})}-\cos{(\log{x})} \right\} \\
\\
\int \sin{(\log{x})} dx&=\frac{1}{2}x\left\{ \sin{(\log{x})}-\cos{(\log{x})} \right\} \\
\end{align}
となり、積分定数$~C~$を加え、
\begin{equation}
\int \sin{(\log{x})} dx=\frac{1}{2}x\left\{ \sin{(\log{x})}-\cos{(\log{x})} \right\}+C \\
\end{equation}
が求まった。
昨年度までより2問ほど減りました。難易度も下がった??

◇参考文献等
・『私学教員適性検査問題集 数学(平成30年度~令和2年度)』
コメント