東京都私学教員適性検査の過去問(令和2年度)の答えを解説付きで載せています。
問題集の解答例で、解法を調べたい際にご活用ください。
大問1
大問2(本ページ)
※大問3~5に関しては、問題集の解答の中に解法まで載っています。
他の年度については、コチラからどうぞ。
サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
解説の内容自体に影響はありません。
問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。
1
(1) $~n=~6~,~14~$
(2) $~AB=\displaystyle \frac{8\sqrt{5}}{5}~$
(3) $~-20~$
(4) $~\displaystyle 3 \leqq a < \frac{7}{2}~$
(5) ①$~f(x)=6x^2-18x+10~$ ②$~a=\displaystyle \frac{1}{2},1,3$
(6) $~a=4~,~b=4\sqrt{2}~$
(7) ①$~3+\sqrt{2}~$ ②$~2\sqrt{14}~$
(8) ①$~120^{\circ}~$ ②$~\displaystyle \frac{13\sqrt{3}}{4}~m^2~$
(9) $~\displaystyle \frac{a(a^2+3b^2)}{3}\pi~$
2(1)
因数分解すると、
\begin{equation}
n^2-20n+91=(n-13)(n-7)
\end{equation}
であり、素数を$~p~$とすると、$~n-13 < n-7 ~$より、
\begin{equation}
(n-13,n-7)=(1,p)~,~(-p,-1)
\end{equation}
となる。
よって、$~n=14~,~6~$が求まった。
2(2)
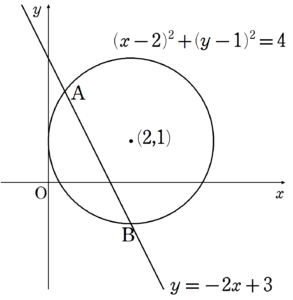
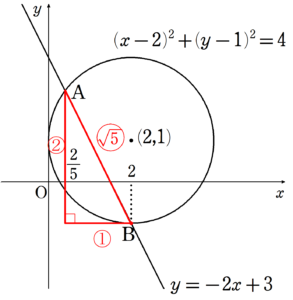
まずは$~A~,B~$の$~x~$座標を求める。
直線の方程式を、円の方程式に代入することで、
\begin{align}
(x-2)^2+(-2x+3-1)^2&=4 \\
(x-2)^2+(-2x+2)^2&=4 \\
x^2-4x+4+4x^2-8x+4&=4 \\
5x^2-12x+4&=0 \\
(5x-2)(x-2)&=0 \\
x&=\frac{2}{5}~,~2~
\end{align}
と求まるため、$~A~$の$~x~$座標が$~\displaystyle \frac{2}{5}~$、$~B~$の$~x~$座標が$~2~$である。
また、直線の傾きが$~-2~$なので、下の図のように直角三角形を考えると、弦$~AB~$の長さは、$~A~$と$~B~$の$~x~$座標の差の$~\sqrt{5}~$倍である。
よって、
\begin{equation}
AB=\left(2-\frac{2}{5} \right) \times \sqrt{5}=\frac{8\sqrt{5}}{5}
\end{equation}
が求まった。
2(3)
$~\displaystyle \left( 2x^2-\frac{1}{2x} \right)^6~$を展開したときに、$~x^3~$が出てくる項は、$~2x^2~$を3回、$~\displaystyle -\frac{1}{2x}~$を3回かけた項。
よって、二項定理から、
\begin{align}
&~~~_6C_3\cdot (2x^2)^3 \cdot \left( -\frac{1}{2x} \right)^3 \\
\\
&=\frac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1}\cdot 8x^6 \cdot \left( -\frac{1}{8x^3} \right) \\
\\
&=-20x^3
\end{align}
となるため、$~x^3~$の係数は$~-20~$と求まった。
2(4)
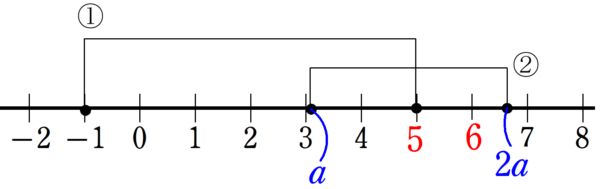
$~a < 2a~$に注意して、それぞれの二次不等式を解くと、
\begin{align}
x^2-4x-5 &\ge 0 \\
(x-5)(x+1) &\ge 0 \\
x \le -1 ~&,~ 5 \le x \cdots ①
\end{align}
\begin{align}
x^2-3ax+2a^2 &\le 0 \\
(x-a)(x-2a) &\le 0 \\
a \le x& \le 2a \cdots ②
\end{align}
となる。
これらを同時に満たす整数$~x~$としてあり得るのは、上の数直線から、$~x=5~,6~$なので、次の不等式が成り立つ。
\begin{align}
6 \le & ~ 2a < 7 \\
3 \le & ~ a < \frac{7}{2}
\end{align}
よって、$~a~$の値の範囲が求まった。
2(5)
①
与式
\begin{equation}
\int_a^xf(t)~dt=2x^3-9x^2+10x-3
\end{equation}
において、両辺を$~x~$で微分することで、
\begin{equation}
f(x)=6x^2-18x+10
\end{equation}
が求まる。
②
①で求めた$~f(t)=6t^2-18t+10~$を左辺に代入すると、
\begin{align}
&~~~\int_a^x 6t^2-18t+10~dt \\
&=\left[ 2t^3-9t^2+10t \right]_a^x \\
&=2x^3-9x^2+10x-2a^3+9a^2-10a
\end{align}
となり、これを与式の右辺と比較することで、
\begin{align}
-2a^3+9a^2-10a&=-3 \\
-2a^3+9a^2-10a+3&=0 \\
2a^3-9a^2+10a-3&=0 \\
(a-1)(2a^2-7a+3)&=0 \\
(a-1)(2a-1)(a-3)&=0 \\
a&=1~,~\frac{1}{2}~,~3
\end{align}
が求まった。
2(6)
$~x \to 1~$のとき、分母は$~0~$に収束するため、分子も$~0~$に収束しなければならない。
($~\frac{0}{0}~$の不定形でないと、$~\sqrt{2}~$に収束しないから。)
よって、分子に$~x=1~$を代入して、
\begin{align}
a\sqrt{1+1}-b&=0 \\
\sqrt{2}a-b&=0 \\
b&=\sqrt{2}a
\end{align}
が成り立つ。これを元の式の左辺に代入して、
\begin{align}
&~~~\lim_{x \to 1}\frac{a\sqrt{x+1}-\sqrt{2}a}{x-1} \\
\\
&=\lim_{x \to 1}\frac{(a\sqrt{x+1}-\sqrt{2}a)(a\sqrt{x+1}+\sqrt{2}a)}{(x-1)(a\sqrt{x+1}+\sqrt{2}a)} \\
\\
&=\lim_{x \to 1}\frac{a^2(x+1)-2a^2}{(x-1)(a\sqrt{x+1}+\sqrt{2}a)} \\
\\
&=\lim_{x \to 1}\frac{a^2x-a^2}{(x-1)(a\sqrt{x+1}+\sqrt{2}a)} \\
\\
&=\lim_{x \to 1}\frac{a^2(x-1)}{(x-1)(a\sqrt{x+1}+\sqrt{2}a)} \\
\\
&=\lim_{x \to 1}\frac{a}{\sqrt{x+1}+\sqrt{2}} \\
\\
&=\frac{a}{\sqrt{2}+\sqrt{2}} \\
\\
&=\frac{a}{2\sqrt{2}} \\
\end{align}
となり、これが$~\sqrt{2}~$となるため、
\begin{align}
\frac{a}{2\sqrt{2}}&=\sqrt{2} \\
a&=4
\end{align}
が求まる。
また、$~b=\sqrt{2}a=4\sqrt{2}~$も求まる。
2(7)
①
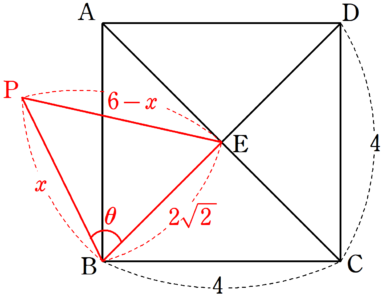
下の図のように、$~\angle PBE=\theta~,~BP=x~$とおく。このとき、$~PE=6-x~$とおける。
$~\triangle PBE~$において、余弦定理を使うと、
\begin{align}
(6-x)^2&=x^2+(2\sqrt{2})^2-2\cdot 2\sqrt{2}\cdot x \cdot \cos{\theta} \\
36-12x+x^2&=x^2+8-4\sqrt{2}x\cos{\theta} \\
36-12x&=8-4\sqrt{2}x\cos{\theta} \\
-12x+4\sqrt{2}x\cos{\theta}&=-28 \\
3x-\sqrt{2}x\cos{\theta}&=7 ~~~~\cdots (*) \\
(3-\sqrt{2}\cos{\theta})x&=7 \\
x&=\frac{7}{3-\sqrt{2}\cos{\theta}}
\end{align}
と表せる。
$~x~$が最大となるのは、分母が最小となるときである。すなわち、$~-1 \le \cos{\theta} \le 1~$より、$~\cos{\theta}=1~~(\theta=0)~$のとき。
\begin{align}
x&=\frac{7}{3-\sqrt{2}} \\
\\
&=\frac{7(3+\sqrt{2})}{(3-\sqrt{2})(3+\sqrt{2})} \\
\\
&=\frac{7(3+\sqrt{2})}{9-2} \\
\\
&=3+\sqrt{2}
\end{align}
よって、$~BP=x~$の最大値が求まった。
②
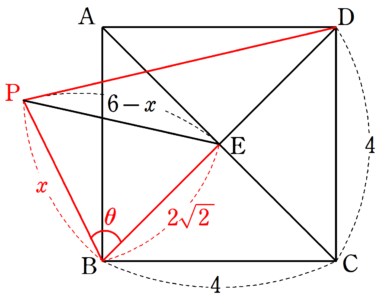
①と同様に、$~\angle PBE=\theta~,~BP=x~$とおく。
このとき、求めたい面積は
\begin{align}
\triangle BPD&=\frac{1}{2}\cdot x \cdot 4\sqrt{2} \cdot \sin{\theta} \\
\\
&=2\sqrt{2}x\sin{\theta} ~~~~\cdots (**)\\
\end{align}
と表せる。
ここで、$~(*)~$より、
\begin{align}
3x-\sqrt{2}x\cos{\theta}&=7 \\
\sqrt{2}x\cos{\theta}&=3x-7 \\
\cos{\theta}&=\frac{3x-7}{\sqrt{2}x}
\end{align}
であり、ここから$~\sin^2{\theta}~$を求めると、
\begin{align}
\sin^2{\theta}+\frac{(3x-7)^2}{2x^2}&=1 \\
\\
\sin^2{\theta}&=\frac{2x^2-(3x-7)^2}{2x^2} \\
\\
\sin^2{\theta}&=\frac{2x^2-9x^2+42x-49}{2x^2} \\
\\
\sin^2{\theta}&=\frac{-7x^2+42x-49}{2x^2}
\end{align}
と表せる。
$~\triangle BPD~$の面積の2乗を考えると、$~(**)~$より、
\begin{align}
(\triangle BPD)^2&=(2\sqrt{2})^2 x^2 \sin^2{\theta} \\
\\
&=8x^2 \cdot \frac{-7x^2+42x-49}{2x^2} \\
&=4(-7x^2+42x-49) \\
&=-28x^2+168x-196 \\
&=-28(x^2-6x)-196 \\
&=-28\{ (x-3)^2-9 \}-196 \\
&=-28(x-3)^2+252-196 \\
&=-28(x-3)^2+56
\end{align}
と平方完成でき、$~0 < x < 6~$より、$~x=3~$のときに$~(\triangle BPD)^2~$は最大値$~56~$をとる。
よって、$~\triangle BPD~$の最大値は$~\sqrt{56}=2\sqrt{14}~$と求まった。
2(8)
①
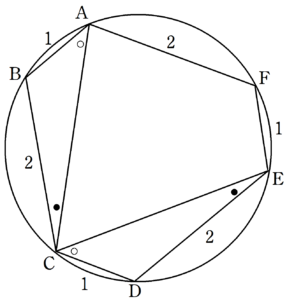
上の図のように、$~\triangle ABC~$と$~\triangle CDE~$において、
$~1~$m の弦の長さを持つ弧に対する円周角より、
\begin{equation}
\angle ACB=\angle CED ~~~\cdots (ⅰ)
\end{equation}
$~2~$m の弦の長さを持つ弧に対する円周角より、
\begin{equation}
\angle BAC=\angle DCE ~~~\cdots (ⅱ)
\end{equation}
$~(ⅰ),(ⅱ)~$より、
\begin{equation}
\angle ABC=\angle CDE ~~~\cdots (ⅲ)
\end{equation}
とわかる。
同様に、
\begin{equation}
\angle ABC=\angle BCD=\angle CDE=\angle DEF=\angle EFA=\angle FAB
\end{equation}
\begin{align}
\angle ABC=\angle BCD=\angle CDE&=\angle DEF \\
&~~~~~~~~~=\angle EFA=\angle FAB
\end{align}
とわかるので、$~6~$角形の内角の和が$~720^{\circ}~$から、
\begin{equation}
\angle ABC=720^{\circ} \div 6 =120^{\circ}
\end{equation}
が求まった。
②
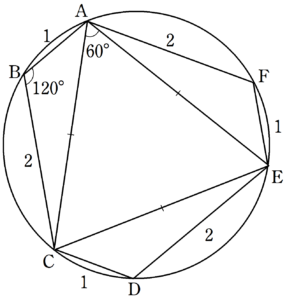
$~(ⅲ)~$と$~AB=CD=1~,~BC=DE=2~$より、$~\triangle ABC \equiv \triangle CDE~$である。
対応する辺より、$~AC=CE~$であり、同様に、
\begin{equation}
AC=CE=EA
\end{equation}
で、$~\triangle ACE~$は正三角形となる。
まずは、$~\triangle ABC ~$の面積を求める。
\begin{align}
\triangle ABC&=\frac{1}{2}\cdot 1 \cdot 2 \cdot \sin{120^{\circ}} \\
\\
&=\frac{\sqrt{3}}{2}
\end{align}
次に、正三角形$~ACE ~$の面積を求めるため、余弦定理で$~AC~$を求めると、
\begin{align}
AC^2&=1^2+2^2-2\cdot 1 \cdot 2 \cos{120^{\circ}} \\
\\
&=5-4 \cdot \left( -\frac{1}{2} \right) \\
\\
&=7
\end{align}
となるため、$~AC=\sqrt{7}~$である。
ここで、「正多角形の面積の公式」より、
\begin{align}
\triangle ACE&=\frac{\sqrt{3}}{4}\cdot (\sqrt{7})^2 \\
\\
&=\frac{\sqrt{3}}{4}\cdot 7 \\
\\
&=\frac{7\sqrt{3}}{4} \\
\end{align}
以上より、六角形$~ABCDEF~$の面積は、
\begin{align}
&~~~\frac{\sqrt{3}}{2} \cdot 3 + \frac{7\sqrt{3}}{4} \\
\\
&=\frac{6\sqrt{3}}{4} + \frac{7\sqrt{3}}{4} \\
\\
&=\frac{13\sqrt{3}}{4} \\
\end{align}
と求まった。
2(9)
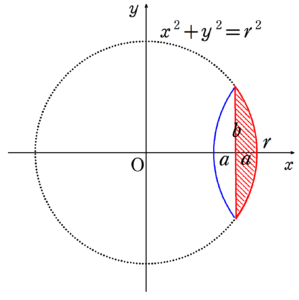
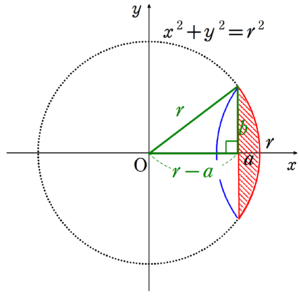
下の図のように、凸レンズの断面図を$~xy~$座標平面上で考える。
この図の赤い斜線部分を$~x~$軸の周りに1回転させた立体を2つ組み合わせれば、求めたい体積が求まるので、
\begin{align}
&~~~2\int_{r-a}^{r} \pi y^2~dx \\
\\
&=2\pi \int_{r-a}^{r} r^2-x^2~dx \\
\\
&=2\pi \left[ r^2x-\frac{1}{3}x^3 \right]_{r-a}^r \\
\\
&=2\pi \left\{ r^3-\frac{1}{3}r^3-r^2(r-a)+\frac{1}{3}(r-a)^3 \right\} \\
\\
&=2\pi \left\{ \frac{2}{3}r^3-r^3+r^2a+\frac{1}{3}(r^3-3r^2a+3ra^2-a^3) \right\} \\
\\
&=2\pi \left(-\frac{1}{3}r^3+r^2a+\frac{1}{3}r^3-r^2a+ra^2-\frac{1}{3}a^3 \right) \\
\\
&=2\pi \left(ra^2-\frac{1}{3}a^3 \right) ~~~\cdots ①
\end{align}
と計算できる。
ここで、$~r~$を$~a~,~b~$で表すことを考える。
上の図で、三平方の定理を使うと、
\begin{align}
r^2&=(r-a)^2+b^2 \\
r^2&=r^2-2ar+a^2+b^2 \\
2ar&=a^2+b^2 \\
r&=\frac{a^2+b^2}{2a}~~~\cdots ②
\end{align}
と求まる。
よって、$②$を$①$に代入して、
\begin{align}
&=2\pi \left(\frac{a^2+b^2}{2a}\cdot a^2-\frac{1}{3}a^3 \right) \\
\\
&=2\pi \left(\frac{a^3}{2}+\frac{ab^2}{2}-\frac{1}{3}a^3 \right) \\
\\
&=2\pi \left(\frac{1}{6}a^3+\frac{ab^2}{2} \right) \\
\\
&=\left(\frac{1}{3}a^3+ab^2 \right) \pi \\
\\
&=\frac{a(a^2+3b^2)}{3} \pi \\
\end{align}
と求まった。
※球欠を2つくっつけた図形なので、公式を知っている人はすぐに解くことができます。(参考:「球欠と球冠」)
(7)と(9)が少し難しめでした。ただ、時間制限がある中だと焦って計算ミスしそうです。

◇参考文献等
・『私学教員適性検査問題集 数学(平成30年度~令和2年度)』
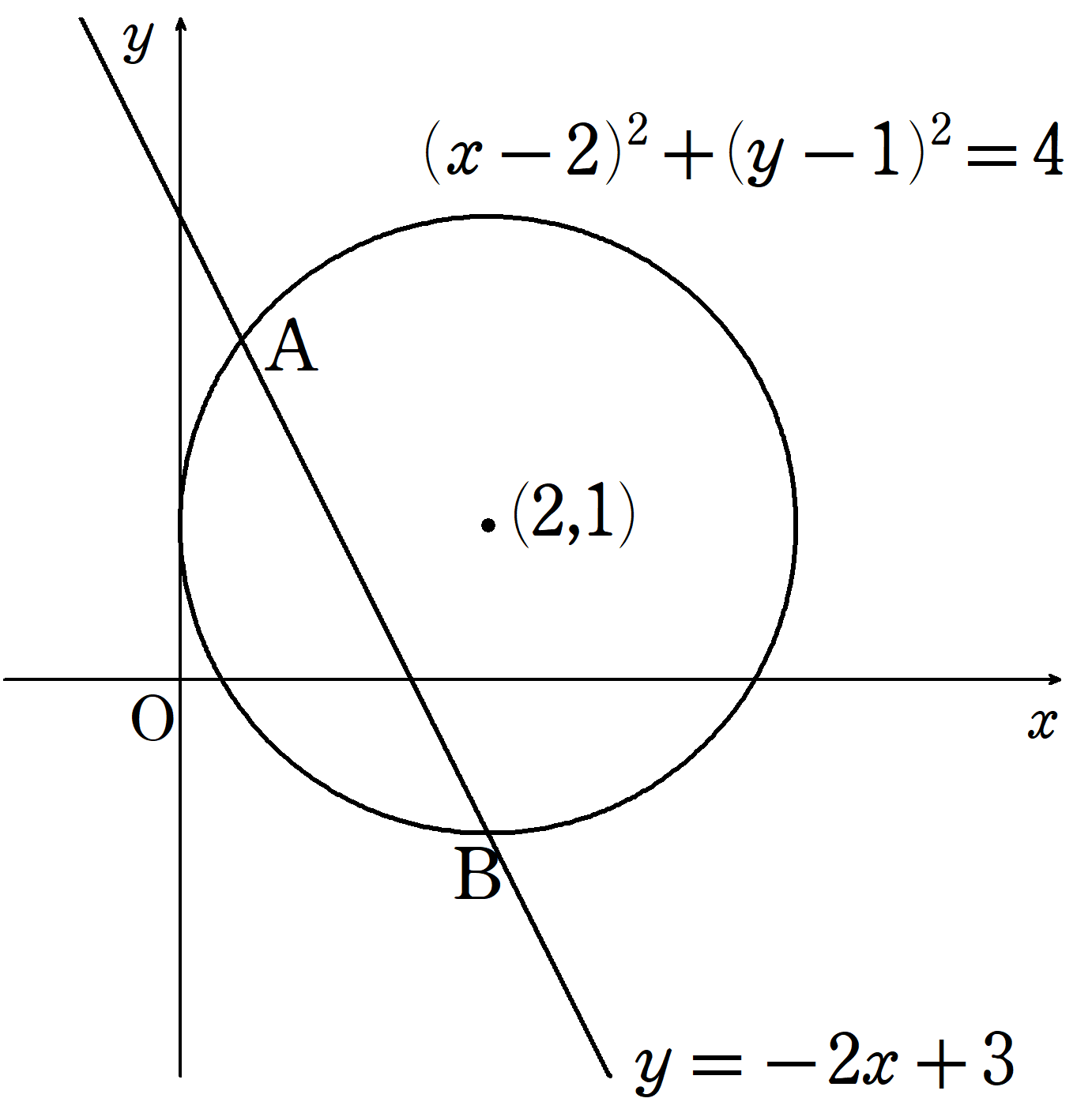
コメント