18°の三角比は近似値を使わずに、値を表すことができます。
その値とは、以下の通り。
\begin{align*}
\sin{18^{\circ}}&=\frac{\sqrt{5}-1}{4} \\
\\
\cos{18^{\circ}}&=\frac{\sqrt{10+2\sqrt{5}}}{4} \\
\\
\tan{18^{\circ}}&=\frac{\sqrt{25-10\sqrt{5}}}{5} \\
\end{align*}この記事では、これらの値がどのように求まるのかを、現役数学教員が解説。
18°の三角比は、36°の三角比に半角の公式を適用するか、36°のときと同じ黄金三角形から直接導くことができます。
- 18°の三角比の値とその近似値
- 半角の公式を利用した求め方
- 黄金三角形を利用した求め方
マイナーな三角比の値を含めた、三角比の値一覧表はこちらから↓↓
18°の三角比の値とその近似値
18°の三角比の値
$~18^{\circ}=\displaystyle \frac{\pi}{10}~$の三角比の値は、二重根号を用いて以下のように表されます。
\begin{align*}
\sin{18^{\circ}}&=\frac{\sqrt{5}-1}{4} \\
\\
\cos{18^{\circ}}&=\frac{\sqrt{10+2\sqrt{5}}}{4} \\
\\
\tan{18^{\circ}}&=\frac{\sqrt{25-10\sqrt{5}}}{5} \\
\end{align*}$~\sin{18^{\circ}}~$だけは、二重根号がなくスッキリとした式になっています。

$~36^{\circ}~$のときと同じように、残り2種類の三角比は二重根号で複雑‥‥。
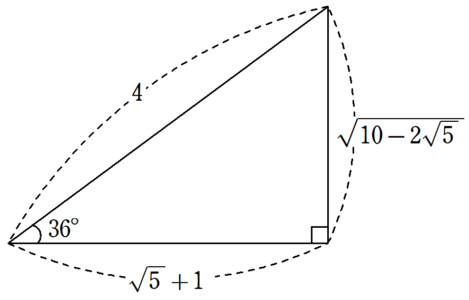
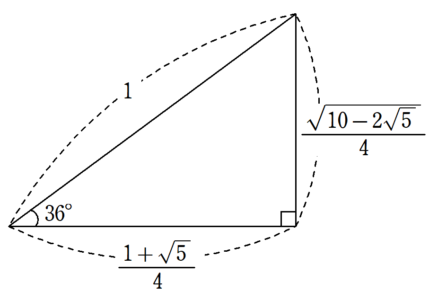
これらの値を基に、斜辺が$~4~$の直角三角形で作ると、図1のようになります。
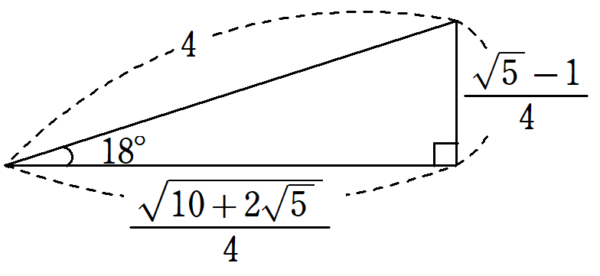
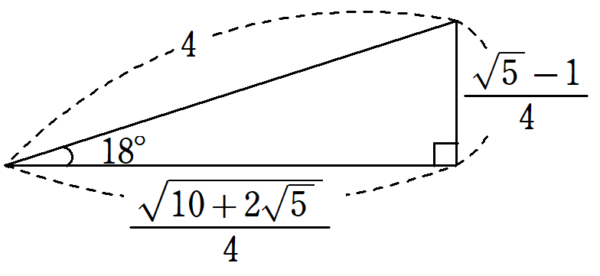
18°の三角比の近似値
18°の三角比の値 の近似値ををExcelで出してみると、図2のようになります。
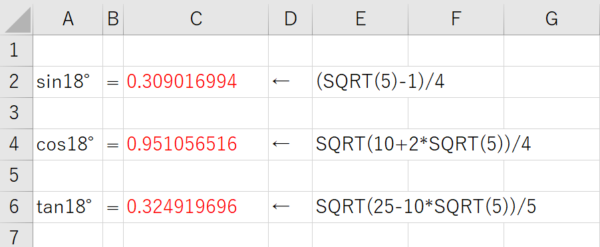

小数第5位を四捨五入すると、教科書に載っている三角比の値と同じ数値が出てきます。
18°の三角比の求め方
求める方法は2つあり、どちらも計算は煩雑です。
半角の公式による求め方
18°は36°の半分であるため、36°の三角比に半角の公式を使うことで、18°の三角比も求めることができます。
\begin{align*}
\sin{36^{\circ}}&= \frac{\sqrt{10-2\sqrt{5}}}{4} \\
\\
\cos{36^{\circ}}&= \frac{\sqrt{5}+1}{4} \\
\\
\tan{36^{\circ}}&=\sqrt{5-2\sqrt{5}} \\
\end{align*}これらの値の求め方に関しては、以下の記事に載せています。

実際に半角の公式にあてはめると以下のような計算となります。
- $~\sin{18^{\circ}}~$の値
半角の公式$~\displaystyle \sin^2{\frac{\theta}{2}}=\frac{1-\cos{\theta}}{2}~$で、$~\theta=36^{\circ}~$とすると、
\begin{align*}
\sin^2{18^{\circ}}&=\frac{1-\cos{36^{\circ}}}{2} \\
\\
&=\frac{1-\frac{1+\sqrt{5}}{4}}{2} \\
\\
&=\frac{4-(1+\sqrt{5})}{8} \\
\\
&=\frac{3-\sqrt{5}}{8} \\
\end{align*}となるため、 $~\sin{18^{\circ}} > 0~$より、
\begin{align*}
\sin{18^{\circ}}&=\frac{\sqrt{3-\sqrt{5}}}{2\sqrt{2}} \\
\\
&=\frac{\sqrt{3-\sqrt{5}}\cdot \sqrt{2}}{2\sqrt{2}\cdot \sqrt{2}} \\
\\
&=\frac{\sqrt{6-2\sqrt{5}}}{4} \\
\\
&=\frac{\sqrt{(\sqrt{5}-1)^2}}{4} \\
\\
&=\frac{|\sqrt{5}-1|}{4} \\
\\
&=\frac{\sqrt{5}-1}{4} \\
\end{align*}が求まる。
- $~\cos{18^{\circ}}~$の値
半角の公式$~\displaystyle \cos^2{\frac{\theta}{2}}=\frac{1+\cos{\theta}}{2}~$で、$~\theta=36^{\circ}~$とすると、
\begin{align*}
\cos^2{18^{\circ}}&=\frac{1+\cos{36^{\circ}}}{2} \\
\\
&=\frac{1+\frac{\sqrt{5}+1}{4}}{2} \\
\\
&=\frac{4+\sqrt{5}+1}{8} \\
\\
&=\frac{5+\sqrt{5}}{8} \\
\end{align*}となるため、 $~\cos{18^{\circ}} > 0~$ より、
\begin{align*}
\cos{18^{\circ}}&=\frac{\sqrt{5+\sqrt{5}}}{2\sqrt{2}} \\
\\
&=\frac{\sqrt{10+2\sqrt{5}}}{4} \\
\end{align*}が求まる。
- $~\tan{18^{\circ}}~$の値
半角の公式$~\displaystyle \tan^2{\frac{\theta}{2}}=\frac{ 1-\cos{\theta} }{1+\cos{\theta}}~$で、$~\theta=36^{\circ}~$とすると、
\begin{align*}
\tan^2{18^{\circ}}&=\frac{1-\cos{36^{\circ}}}{1+\cos{36^{\circ}}} \\
\\
&=\frac{1-\frac{\sqrt{5}+1}{4}}{1+\frac{\sqrt{5}+1}{4}} \\
\\
&=\frac{4-\sqrt{5}-1}{4+\sqrt{5}+1} \\
\\
&=\frac{(3-\sqrt{5})(5-\sqrt{5})}{(5+\sqrt{5})(5-\sqrt{5})} \\
\\
&=\frac{15-8\sqrt{5}+5}{25-5} \\
\\
&=\frac{20-8\sqrt{5}}{20} \\
\\
&=\frac{5-2\sqrt{5}}{5} \\
\end{align*}となるため、 $~\tan{18^{\circ}} > 0~$ より、
\begin{align*}
\tan{18^{\circ}}&=\frac{\sqrt{5-2\sqrt{5}}}{\sqrt{5}} \\
\\
&=\frac{\sqrt{5-2\sqrt{5}}\cdot \sqrt{5}}{\sqrt{5}\cdot \sqrt{5}} \\
\\
&=\frac{\sqrt{25-10\sqrt{5}}}{5} \\
\end{align*}が求まる。



分母の有理化が多くて、計算が大変だね‥‥。
黄金三角形による求め方
計算ゴリ押しの方法ではなく、黄金三角形を用いた、幾何的な求め方もあります。
sin18°の求め方
図3のような$~AB=AC=1~,~\angle{A}=36°~$の$~\triangle ABC~$を考える。
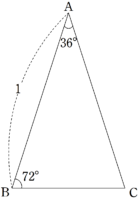

$~\angle{B}~$の二等分線と$~AC~$の交点を$~D~$とする。
このとき、$~\triangle BCD~$や$~\triangle DAB~$も二等辺三角形となるので、$~BC=BD=AD=1~$である。
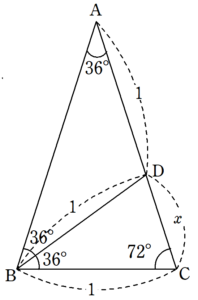

また、$~CD=x~$とすると、$~\triangle ABC~$∽$~ \triangle BCD~$より、
\begin{align*}
(1+x)1&=1:x \\
x(1+x)&=1 \\
x^2+x-1&=0 \\
x&=\frac{-1 \pm \sqrt{5}}{2}
\end{align*}となり、$~x > 0~$より、$~x=\displaystyle \frac{\sqrt{5}-1}{2}~$が求まる。
次に、$~B~$ から$~AC~$におろした垂線の足を$~E~$とすると、$~E~$は$~DC~$の中点であり、$~\angle CBD=36^{\circ}~$を二等分する。
よって、$~\displaystyle EC=\frac{1}{2}x=\frac{\sqrt{5}-1}{4}~$ となる。
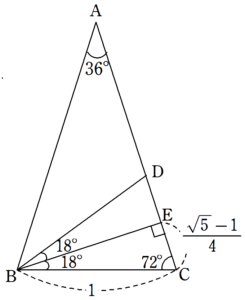

図5で、直角三角形$~BEC~$に注目すれば、
\begin{align*}
\sin{18^{\circ}}&=\frac{CE}{1} \\
\\
&=CE \\
\\
&=\frac{\sqrt{5}-1}{4}
\end{align*}と求めることができる。



36°の三角比のときと同じ図を使っているよ。
cos18°、tan18° の求め方
$~\sin{18^{\circ}}~$が求まってしまえば、あとは三角比の相互関係を使うことで、$~\cos{18^{\circ}}~,~\tan{18^{\circ}}~$も求めることができます。
- $~\cos{18^{\circ}}~$の値
$~\sin^2{18^{\circ}}+\cos^2{18^{\circ}}=1~$なので、
\begin{align*}
\cos^2{18^{\circ}}&=1-\left( \frac{\sqrt{5}-1}{4} \right)^2 \\
\\
&=1-\frac{5-2\sqrt{5}+1}{16} \\
\\
&=\frac{10+2\sqrt{5}}{16}
\end{align*}であり、$~\cos{18^{\circ}} > 0~$より、
\cos{18^{\circ}}=\frac{\sqrt{10+2\sqrt{5}}}{4}が求まる。
- $~\tan{18^{\circ}}~$の値
$~\tan{18^{\circ}}=\displaystyle \frac{\sin{18^{\circ}}}{\cos{18^{\circ}}}~$なので、
\begin{align*}
\tan{18^{\circ}}&=\frac{\frac{\sqrt{5}-1}{4}}{\frac{\sqrt{10+2\sqrt{5}}}{4}} \\
\\
&=\frac{\sqrt{5}-1}{\sqrt{10+2\sqrt{5}}} \\
\\
&=\frac{(\sqrt{5}-1)\sqrt{10-2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\sqrt{10-2\sqrt{5}}} \\
\\
&=\frac{\sqrt{(10-2\sqrt{5})(\sqrt{5}-1)^2}}{\sqrt{100-20}} \\
\\
&=\frac{\sqrt{(10-2\sqrt{5})(6-2\sqrt{5})}}{\sqrt{80}} \\
\\
&=\frac{\sqrt{80-32\sqrt{5}}}{4\sqrt{5}} \\
\\
&=\frac{4\sqrt{5-2\sqrt{5}}\cdot \sqrt{5}}{4\sqrt{5}\cdot \sqrt{5}} \\
\\
&=\frac{\sqrt{25-10\sqrt{5}}}{5}
\end{align*}が求まる。
$~sin^{18^{\circ}}~$だけは、黄金三角形からきれいに求まりましたが、他の2つに関しては半角の公式と同様の計算量となってしまいます。



さらに半分にして、9°とかを考えると、もっと計算大変なんだろうなぁ。



実際にやってみると、$~\sin{9^{\circ}}=\displaystyle \frac{\sqrt{8-2\sqrt{10+2\sqrt{5}}}}{4}~$で三重根号になるよ。
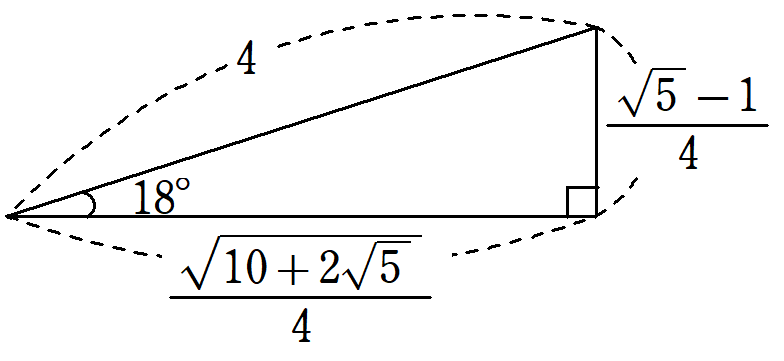
コメント