人々が美しさを感じ、$~\displaystyle 1:\frac{1+\sqrt{5}}{2}~$で表される黄金比。
正五角形では、この黄金比がいたるところに登場します。
特に、正五角形に5本の対角線をひくことでできる星型の図形の中には、「黄金三角形」と呼ばれる二等辺三角形が20個も隠れており、紀元前の数学者ピタゴラスが自身の教団のシンボルマークにするほど好んでいました。
この記事では、正五角形の中に隠れる黄金比を計算によって求めつつ、星型の図形で登場する黄金三角形20個の場所まで解説。
ピタゴラスが魅了された、正五角形の美しい性質について理解することができます。
黄金比の定義と歴史
正五角形と黄金比の関係性を知る前に、黄金比の基本的知識を確認しておきましょう。
黄金比は人が最も美しいと感じる比率
黄金比、黄金数の定義は以下のようになっています。
次の値で表される比を黄金比という。
1:\frac{1+\sqrt{5}}{2}また、$~\displaystyle \frac{1+\sqrt{5}}{2}~$のことを黄金数といい、ギリシャ文字$~\phi~$(ファイ)で表す。
黄金数$~\displaystyle \phi=\frac{1+\sqrt{5}}{2}~$は無理数であり、その近似値は
\phi =1.618033988~\cdots
となります。
黄金比という名称は、ドイツの数学者マルティン・オーム(Martin Ohm, 1792~1872)によって付けられたものです。
しかし、$~1:\phi~$こそ人が最も美しいと感じる比であるという考え方は、古代ギリシャまでさかのぼります。
黄金比を最初に研究したのはピタゴラス
黄金比の美しさを最初に活用したのは、彫刻家フェイディアス(Pheidias , B.C.490頃~B.C.430頃)であり、彼が建設を主導したパルテノン神殿は正面からの縦横比が$~1:\phi~$となっています。

(出典:Steve Swayne, CC BY 2.0, via Wikimedia Commons)
黄金数に$~\phi~$が使われているのも、フェイディアスをギリシャ文字で表した “$\phi \epsilon \iota \delta \iota \alpha \zeta$” の頭文字に由来しています。
ただ、 フェイディアスより前に、黄金比に美しさを感じていた人物がいました。
その人物こそ、古代ギリシャの数学者ピタゴラス(Pythagoras , B.C.569頃~B.C.500頃)です。

(出典:The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons)
ピタゴラスは正五角形が神秘的な図形であり、コンパスと定規だけで作図ができることに感動し、図3の図形をピタゴラス教団のシンボルマークにしました。
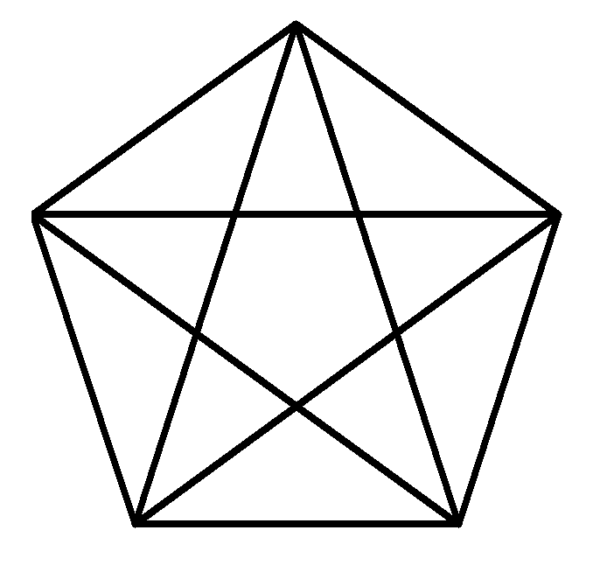
ピタゴラスの感性はとても鋭く、図3の図形の中には黄金比がたくさん隠れています。(後述)

正五角形の対角線の長さ
ピタゴラスが美しさを感じた正五角形。
美しさの最大の理由は対角線の長さにありました。
辺と対角線の長さの比は黄金比
ピタゴラスは以下の性質について、気づいていたことがわかっています。
正五角形の辺と対角線の長さの比は、$~1~:~\phi~$となる。
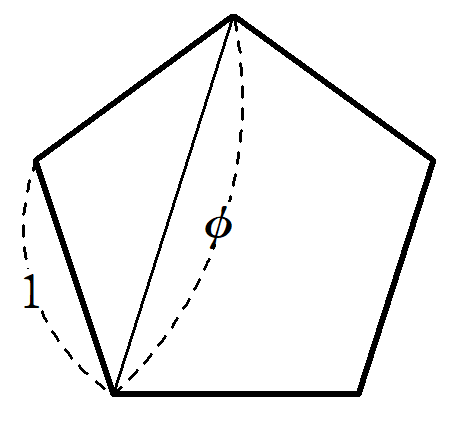
正五角形の辺と対角線の長さの比は黄金比($~1:\phi~$)となります。
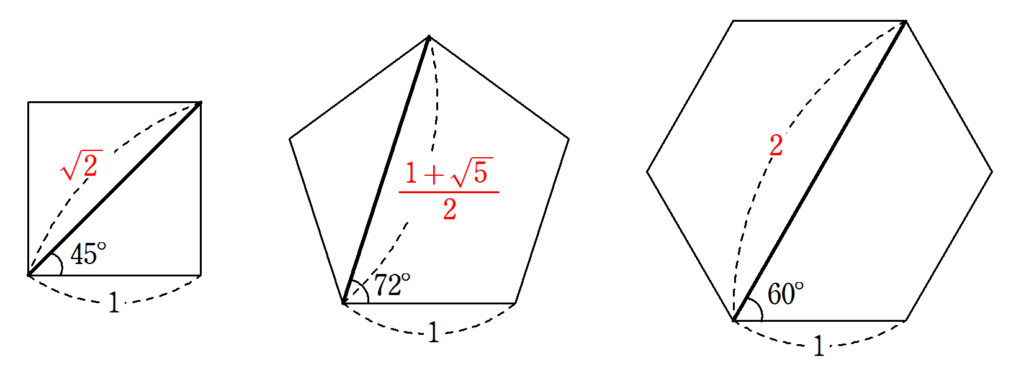
正五角形と黄金比を結び付ける最も有名な性質で、正四角形(正方形)や正六角形と比べ、正五角形は図形的に複雑であることがわかるでしょう。
正五角形の対角線の長さは相似から求められる
一辺が$~1~$の正五角形の対角線の長さは、中学3年生で習う「相似」の知識で求めることができます。
一辺が$~1~$の正五角形$~ABCDE~$で、対角線$~AC~,~AD~$を引き、$~\angle ACD~$の二等分線と$~AD~$の交点を$~F~$とすると、図6のように角度が求まる。

対角線$~AC=x~$とおくと、$~\triangle ACD~$と$~\triangle CDF~$が二等辺三角形であるため、図7のように辺の長さがおける。

ここで、二角相等より$~\triangle ACD~$∽$~\triangle CDF~$のため、
\begin{align*}x:1&=1:(x-1) \\x(x-1)&=1 \\x^2-x-1&=0 \\x&=\frac{1\pm\sqrt{5}}{2}\end{align*}が求まり、$~x > 1~$から、$~\displaystyle x=\frac{1+\sqrt{5}}{2}=\phi~$となる。
補助線によって登場する二等辺三角形や、相似の性質を使うことで二次方程式が作られ、その解に黄金数$~\phi~$が現れました。
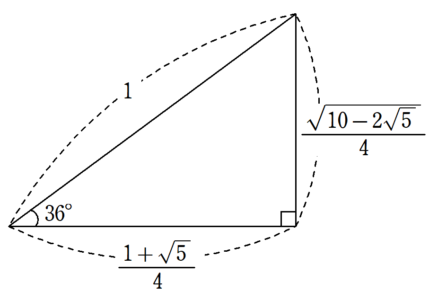
ちなみに、図7をさらに発展させることで、$~36^{\circ}~$の三角比についても求めることができます。
Ⅲ 正五角形の対角線の分割
正五角形の辺と対角線の関係に黄金比が現れましたが、実は対角線そのものにも黄金比が隠れています。
各対角線が黄金比で分割されている
正五角形の対角線は全部で5本引けますが、その5本が互いに黄金比になるよう分割し合っているという性質です。
正五角形の対角線は、それと交わる2本の対角線によって、$~\phi~:~1~:~\phi~$に分割される。
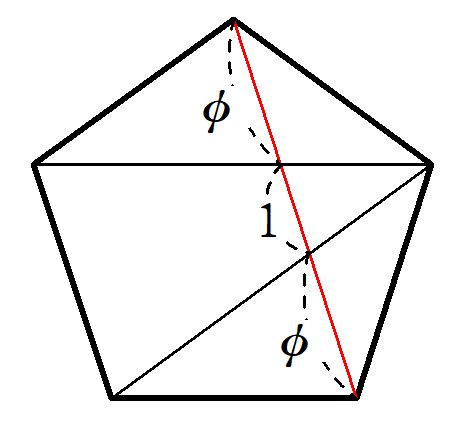
この性質について、5本の対角線それぞれで考えると、以下のような色分けが可能です。
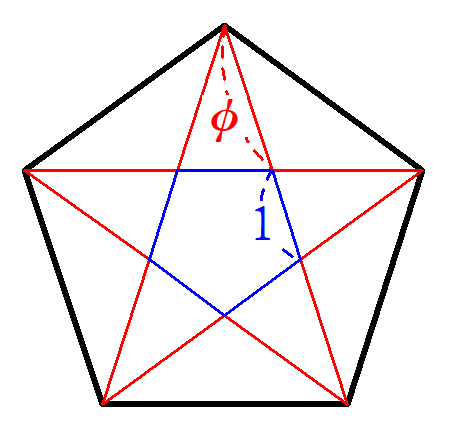
図9はまさにピタゴラス教団のシンボルマーク。(図3と同様)
内部にできる五角形の1辺の長さを$~1~$とすると、$~\phi~$の長さを持つ線分で星形ができているのが、美しいですね。
各線分の長さは計算で求められる
なぜ黄金比で分割されるのかは、各線分の長さを計算することでわかります。
一辺が$~1~$の正五角形$~ABCDE~$の対角線$~AD~$と、$~BE~,~CE~$の交点をそれぞれ$~F~,~G~$とする。

ここで、正五角形の対角線の求め方の図7より、次の図11のように辺の長さがわかる。

したがって、
\begin{align*}
DF&=AD-AF \\
\\
&=\frac{1+\sqrt{5}}{2}-1 \\
\\
&=\frac{-1+\sqrt{5}}{2}
\end{align*}であり、図形の対称性から、
AG=DF=\frac{-1+\sqrt{5}}{2}となる。
さらに、
\begin{align*}GF&=AF-AG \\\\&=1-\frac{-1+\sqrt{5}}{2} \\&=\frac{3-\sqrt{5}}{2}\end{align*}であるため、求めたい$~AG:GF~$は、
\begin{align*}&~~~AG:GF \\\\&=\frac{-1+\sqrt{5}}{2} : \frac{3-\sqrt{5}}{2} \\\\&=-1+\sqrt{5} : 3-\sqrt{5} \\\\&=\frac{-1+\sqrt{5}}{3-\sqrt{5}}:1 \\\\&=\frac{(-1+\sqrt{5})(3+\sqrt{5})}{(3-\sqrt{5})(3+\sqrt{5})}:1 \\\\&=\frac{2+2\sqrt{5}}{4}:1 \\\\&=\frac{1+\sqrt{5}}{2}:1 \\\\&=\phi : 1\end{align*}となる。
$~AG=DF~$より、
AG:GF:FD=\phi:1:\phi
が求まった。
確かに、1本の対角線が他の2本の対角線との交点により、$~\phi~:~1~:~\phi~$に分割されることがわかりました。
各線分の長さは二次方程式でも求められる
上記の方法のように、直接長さを求めると計算が大変なので、$~\phi~$を求めるための二次方程式$~x^2-x-1=0~$を作るという求め方もあります。
正五角形$~ABCDE~$の対角線をすべて引き、内部にできる正五角形の一辺を$~1~$とする。
$~AD~$と$~CE~$の交点を$~F~$とし、$~DF=x~$とすると、図形の対称性から図12のように$~x~$がおける。

このとき、$~\triangle ACD~$∽$~\triangle CDF~$より、
\begin{align*}AD:CF&=CD:DF \\(2x+1):(x+1)&=x:1 \\(x+1)x&=2x+1 \\x^2+x&=2x+1 \\x^2-x-1&=0\end{align*}という関係式が導かれ、これを解くことで$~x=\phi~$が求まる。
こちらのほうが証明としてはエレガントです。
以上の2通りの方法で、正五角形の対角線がそれぞれ黄金比で分割されていることがわかりました。
正五角形内にある二等辺三角形
図12からもわかるように、正五角形の対角線をすべて引くと、二等辺三角形がたくさん現れます。
何個の二等辺三角形が隠れているのでしょうか?
黄金三角形という名前がついている
これまでの計算で利用してきた細長い二等辺三角形には、「黄金三角形」という名前が定義されています。
3つの内角が$~36^{\circ}~,~72^{\circ}~,~72^{\circ}~$である二等辺三角形を黄金三角形という。
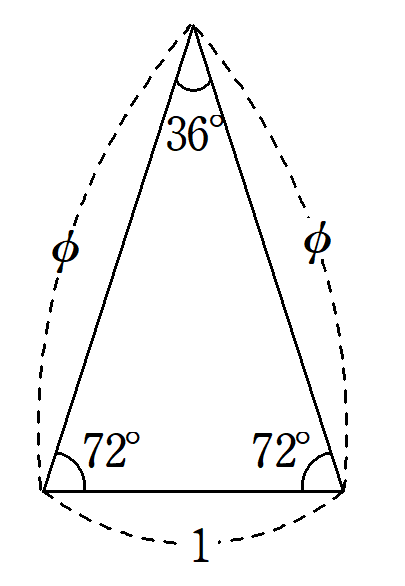
正五角形の1つの頂点から、2本の対角線を引くことで作られる三角形です。
そのため、底辺の長さを$~1~$とすれば、他の2つの辺の長さは黄金数$~\phi~$となります。
二等辺三角形は計35個ある
黄金三角形は、対角線をすべて引いた正五角形の中に、大小含めたくさん現れます。
実際に個数を数えてみると、図14~図16のように黄金三角形は合計20個。
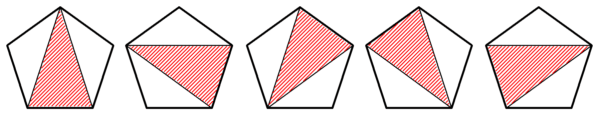
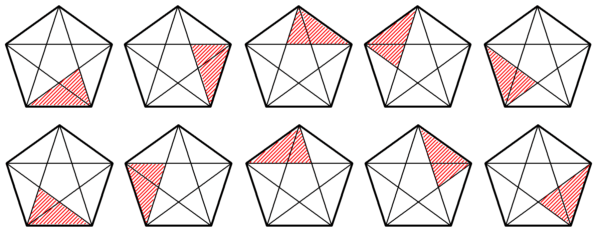
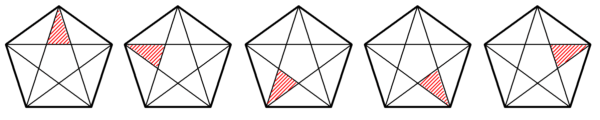
さらに、$~36^{\circ}~,~36^{\circ}~,~108^{\circ}~$の鈍角二等辺三角形は合計15個あります。(図17,図18)
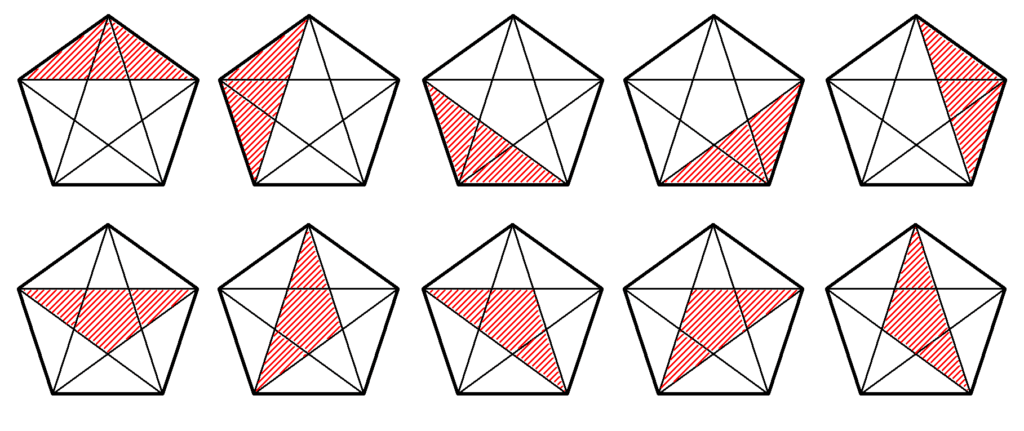
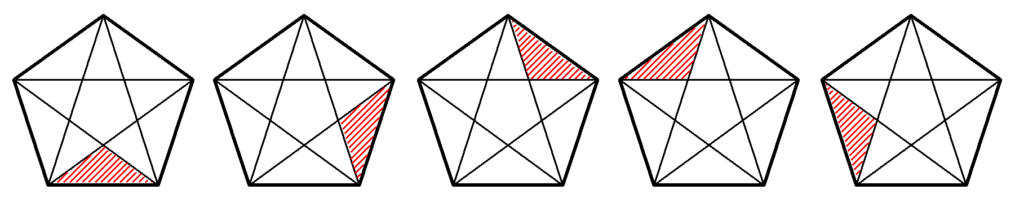
以上より、対角線をすべて引いた正五角形が含む二等辺三角形の個数は35個。
これほどまで多くの二等辺三角形を含んでいるところにも、正五角形や黄金比の美しさを感じますね。
まとめ
正五角形と黄金比の関係について解説してきました。
- 正五角形の一辺と対角線の長さの比は黄金比。
- 正五角形の5本の対角線は、互いに黄金比になるよう分割し合っている。
- 対角線を引いた正五角形には、二等辺三角形が35個存在する。
正五角形は黄金比に関する性質をいくつも持っており、ピタゴラスも魅了されるほど美しい図形であることがわかりました。


値としては、$~\displaystyle \frac{1+\sqrt{5}}{2}~$という複雑な数だけど、正五角形の中で考えると美しいね。



ピタゴラスが使いたがるのもわかるよね。
ただその一方で、有理数でない$~\displaystyle \frac{1+\sqrt{5}}{2}~$の扱いに困っていたんだ。
◇参考文献等
・三浦伸夫・三宅克哉監訳,久村典子訳(2018)『メルツバッハ&ボイヤー 数学の歴史Ⅰー数学の萌芽から17世紀前期までー』,pp.47-48,朝倉書店.
・ピエルジョルジョ・オーディフレッディ著,河合成雄訳(2021)『幾何学の偉大なものがたり』,pp82-85,創元社.

コメント