数を書き表すことができた古代エジプトでは、加減乗除の演算アルゴリズムも誕生しました。
必要な数だけ数字を並べていくヒエログリフの特質上、たし算・ひき算は簡単に行えます。
しかし、電卓や現代の筆算技術がないこの時代、かけ算やわり算は「2倍法」と呼ばれる独自の方法で行っていました。
この記事では、古代エジプトの加減乗除のアルゴリズムをそれぞれ現役数学教員で、数学史の先生であるFukusukeが解説します。
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊
重刷、ブログ累計200万PV達成 - 行間がなくなるほど丁寧な式変形で執筆中
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊は発売1ヶ月で即重刷
- 当数学史ブログは累計200万PV達成
- 行間がなくなるほど丁寧な式変形で記事を執筆
『世界を変えた数学史図鑑』『教養としての数学史』好評発売中！
丸善日本橋店の2025年ベストセラー（理工書部門）に選ばれました！
（理工書部門）に選ばれました！
たし算・ひき算は同じ絵を合わせるだけ
古代エジプトの数字としては、ヒエログリフとヒエラティックが並行して発展しました。
しかし、たし算・ひき算をするうえで実用的だったのはヒエログリフと考えられています。
たし算・ひき算のルール
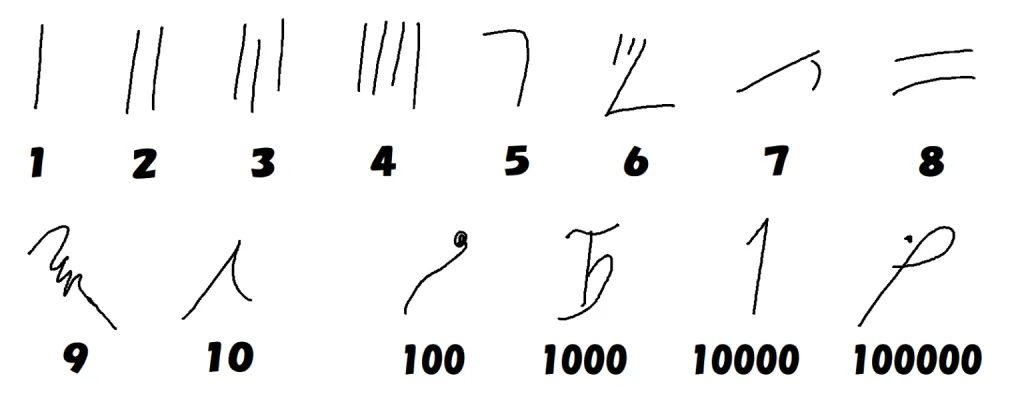
$~10~$のべき乗ごとに異なるヒエログリフ（絵）が用意されていたため、古代エジプトのたし算・ひき算は次の方法で行っていました。
- 同じ種類の絵どうしをたすorひく
- 同じ絵が１０個揃ったら、１つ大きい位の絵を１つ増やす
現在のたし算・ひき算で、上のルールを置き換えてみると、非常に似ていることがわかります。
- 同じ位の数どうしをたすorひく
- 同じ位で１０が作れたら、１つ大きい位に＋１する
古代エジプトも10進法であり、ヒエログリフでは$~1~,~10~,100~,~1000~,\cdots~$を表す数字を必要な分だけ並べて数を表していたため、今とほとんど変わらない分かりやすい計算方法でした。
たし算・ひき算の計算例
実際に、たし算・ひき算の例をいくつか見てみましょう。
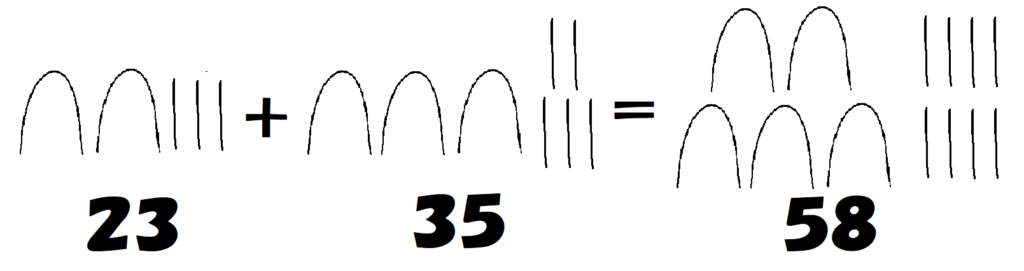
確かに同じ種類の絵どうしをたしている（まとめている）だけで、たし算が可能です。
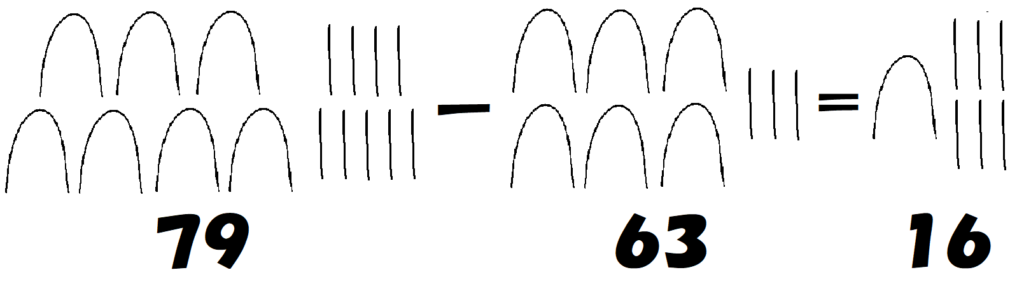
ひき算についても同様で、同じ種類の絵どうしをひいています。
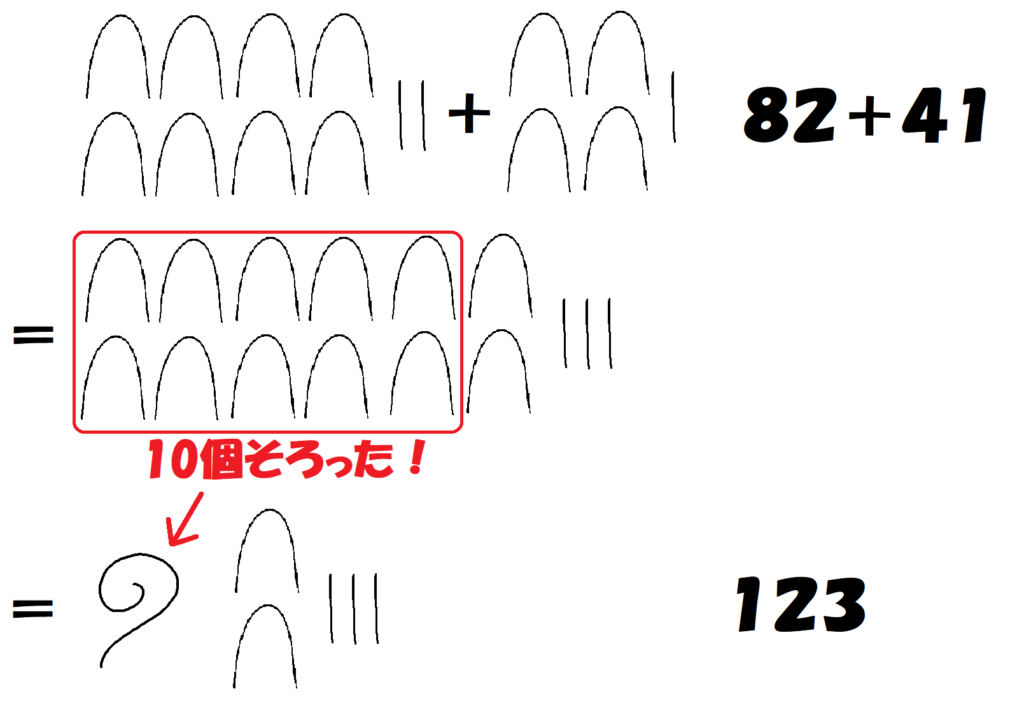
同じ種類の絵が１０個そろうと、１つ上の絵にランクアップします。（繰り上がり）
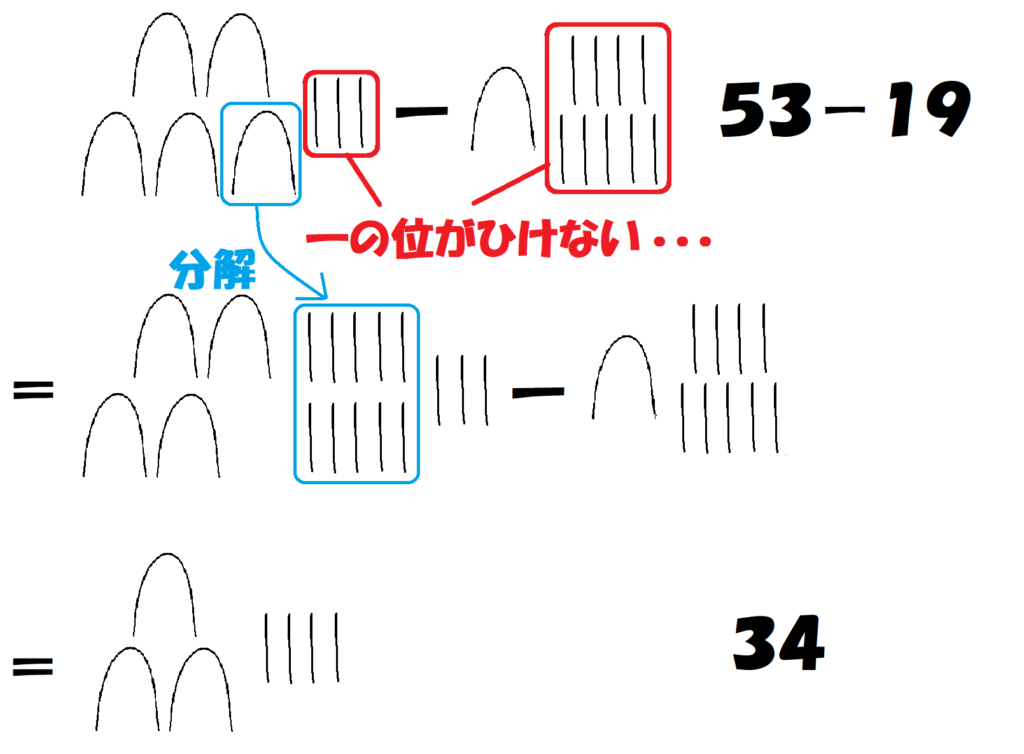
ひくことができない場合、１つ上の絵を分解してひけるようにします。（繰り下がり）
ちなみにですが、$~+~$や$~=~$といった記号ができたのは16世紀であり、古代エジプトでは単に数を並べるだけで計算を表現していました。
ヒエラティックは一の位が計算に適さなかった
古代エジプトのたし算・ひき算では、基本的に同じ絵どうしで計算するため、$~1~$～$~9~$をすべて異なる数字で表していたヒエラティックは適しませんでした。
ただ、当時文字を書けたのは役人階級だけであったため、専用の加減表を使ったり、加減の結果を暗記していたりという可能性もあります。
かけ算・わり算は「2倍法」で効率的に計算した
かけ算はたし算で表すことができます。（例：$~73 \times 4=73+73+73+73~$）
そのため、先述の方法で計算することも可能ですが、あまりにも非効率です。
古代エジプトでは、少しでも効率的にかけ算を行うために、独特な計算方法を用いていました。
2のべき乗倍の結果を組み合わせるかけ算
古代エジプトで使われていた「2倍法」は、かけられる数の$~2~$のべき乗倍リストを作って、必要な数だけを選んでたすという計算方法です。
こちらも例を見てみましょう。（数字は現在のもので表しています）
$~41\times 23~$を計算する。
まず、$~41 \times (2~のベキ乗)~$のリストを作る。（かける数が$~23~$を超える手前まで）
\begin{align*}
41 \times 1&=41~~~~~\cdots ① \\
41 \times 2&=82~~~~~\cdots ②※ \\
41 \times 4&=164~~~~~\cdots ③ \\
41 \times 8&=328~~~~~\cdots ④ \\
41 \times 16&=656~~~~~\cdots ⑤ \\
\end{align*}※$①$の答えの$41$を２つたし合わせることで、$②$の$~41 \times 2=82~$が求まる。この繰り返しにより、表を作っていく。
次に、$~23~$を$~2~$のベキ乗の和で表すと、
23=16+4+2+1
なので、$~⑤+③+②+①~$より、
\begin{align*}
41 \times (16+4+2+1)&=656+164+82+41 \\
41 \times 23&=943
\end{align*}と求まる。
かけ算をたし算に戻して考えるうえで、非常に効率的な方法となっています。
もう１つ例を挙げます。
$~15 \times 10~$を計算する。
まず、$~15 \times (2~のベキ乗)~$のリストを作る。（かける数が$~10~$を超える手前まで）
\begin{align*}
15 \times 1&=15~~~~~\cdots ① \\
15 \times 2&=30~~~~~\cdots ② \\
15 \times 4&=60~~~~~\cdots ③ \\
15 \times 8&=120~~~~~\cdots ④ \\
\end{align*}次に、$~10~$を$~2~$のベキ乗の和で表すと、
10=8+2
なので、$~④+②~$より、
\begin{align*}
15 \times (8+2)&=120+30 \\
15 \times 10&=150
\end{align*}と求まる。
今なら数秒で終わるかけ算でも、古代エジプトでは、それなりの時間と作業を要していることがわかります。
わり算では2のべき乗倍の結果を引いていく
わり算においても、「2倍法」を活用していました。
具体的には、わる数の2のべき乗倍リストを作って、わられる数からひいていくという計算方法です。
例５の逆の計算を考えてみましょう。
$~943 \div 41~$を計算する。
まず、$~41 \times (2~のベキ乗)~$のリストを作る。（積が$~943~$を超える手前まで）
\begin{align*}
41 \times 1&=41~~~~~\cdots ① \\
41 \times 2&=82~~~~~\cdots ② \\
41 \times 4&=164~~~~~\cdots ③ \\
41 \times 8&=328~~~~~\cdots ④ \\
41 \times 16&=656~~~~~\cdots ⑤ \\
\end{align*}次に、$~943~$からリストの数字を大きいものからひいていく。
- $~943-656=287~$より、$~41 \times 16~$がとれる。
- $~287-328~$はできないので、$~41 \times 8~$はとれない。
- $~287-164=123~$より、$~41 \times 4~$がとれる。
- $~123-82=41~$より、$~41 \times 2~$がとれる。
- $~41-41=0~$より、$~41 \times 1~$がとれる。
以上より、$~943~$から$~41~$を$~16+4+2+1=23~$個とれるため、
943 \div 41=23
が求まる。
このように、$~943 \div 41~$という割り算を「$~41~$を何回かけたら$~943~$になるか？」という視点で考えていました。
「2倍法」は12～13世紀まで使われた
古代エジプトで確立した「2倍法」によるかけ算・わり算は、12～13世紀まで広く使われていました。
中国の算木、古代ローマの計算盤といった道具を使わずに計算する場合、この「2倍法」が単純で効率的に計算できる手段だったからです。
（出典：Photographer: Mike Cowlishaw (aus der englischen Wikipedia), CC BY-SA 3.0, via Wikimedia Commons）
しかし、12～13世紀頃にアラビア数字（現在の数字）が広まり、現在の筆算が登場したことで、「2倍法」は取って代わられました。
まとめ・参考文献
古代エジプトの加減乗除の方法について解説してきました。
- たし算・ひき算は同じ絵どうしで行った。
- かけ算・わり算は「2倍法」を使って、効率的に計算していた。
現在の筆算に比べれば時間はかかるものの、アラビア数字がない中で独自の計算アルゴリズムを確立していた点は驚くべきことです。
次の記事では、わり算でわりきれないときに必要な分数について解説します。
たし算・ひき算は絵合わせゲームみたいだね！
カゴの取っ手（十の位）を10個揃えると、繰り上がりでロープ（百の位）になるのはイメージしやすいけど、葦（一万の位）が10個でオタマジャクシ（十万の位）は理解しづらい‥‥。
コメント