【数学史5-3】古代中国で使われた「算木」とは？その使い方と歴史を解説！

　電卓どころか筆算の文化すらなかった古代。

　この記事では、算木を使ったたし算やかけ算の計算方法を紹介するとともに、算木での負の数の表し方や算木の歴史を解説！

　算木からも古代中国の数学力の高さを計り知ることができます。　

当ブログ管理人Fukusukeの2冊目の著書が6月11日に発売！
数学史×世界史の新感覚ノンフィクション！

Amazonで『教養としての数学史』を見る

楽天市場で『教養としての数学史』を見る

算木とは？

　エジプトではヒエログリフによる筆算、バビロニアでは数表の活用により、四則演算を行っていました。

　古代中国では、そろばんの前身である算木という道具を使って、自在に計算を行っています。

算木は古代中国から使われた計算道具

　紀元前2世紀頃から、古代中国人は数を表したり、計算を行ったりするために算木と呼ばれる短い棒を使い始めました。

　右から一の位、十の位、百の位、‥‥と、算木で数字をつくる（図1）ことにより、どんな数でも表すことができます。

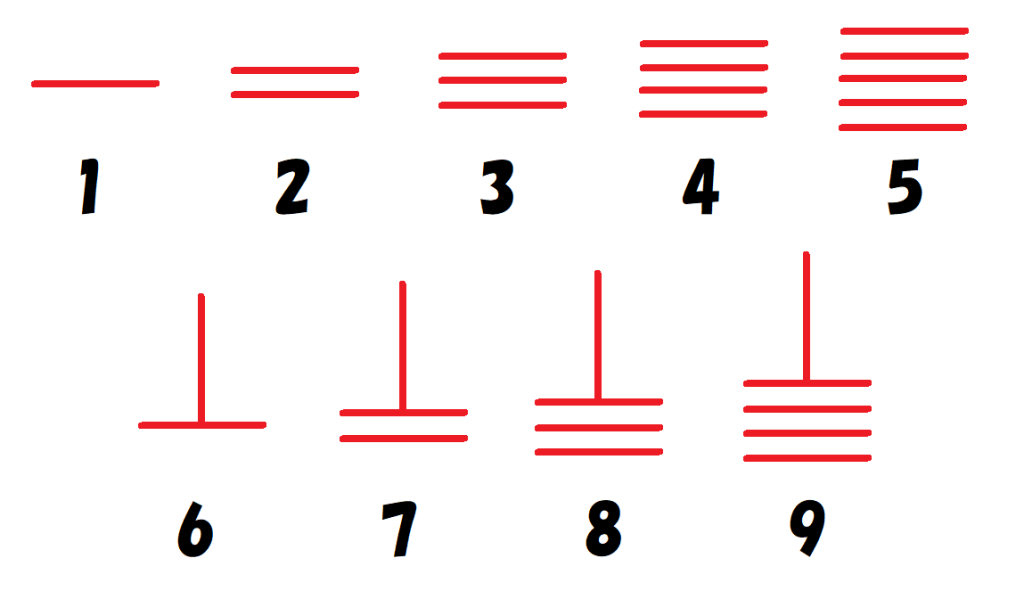
　算木は計算をする際に大量に必要なため、手に入りやすい木材や骨が材料として使われました。
　また、碁盤のような正方形のマス目上に算木を並べて計算をするため、位取りがわかりやすくなっています。

縦式と横式で位を交互に表現した

　算木で数字を表す方法は2種類あり、1つは図1で示した横式（”宗“と呼ばれた）と、もう1つは図2で示す縦式（”衡“と呼ばれた）でした。

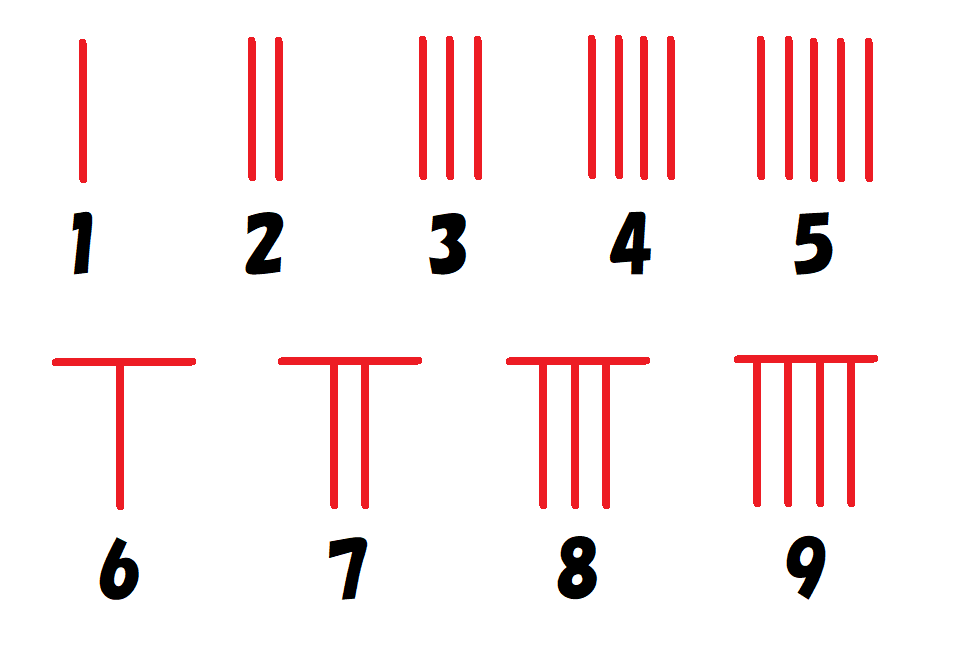
　一の位は縦式、十の位は横式、百の位は縦式、…‥と縦式と横式を交互に使用することで、位の見間違いを防ぎました。

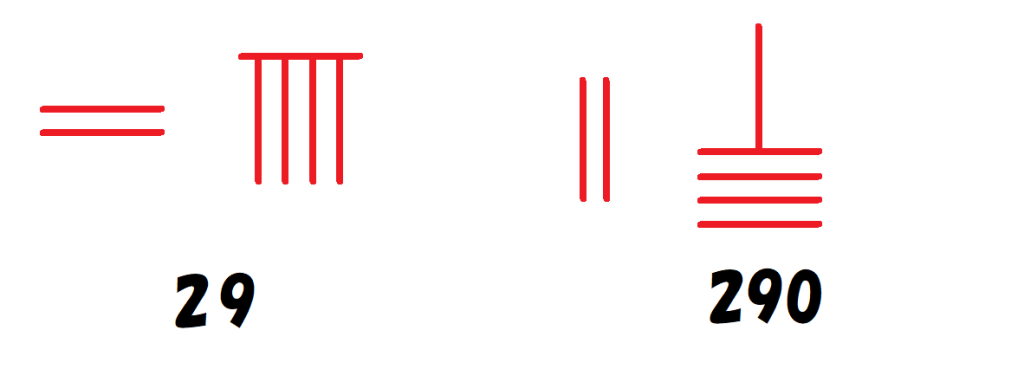
　また、算木を置かないことで「空所（$~0~$）」を表すため、バビロニアと比べて$~0~$の位がわかりやすいという利点を持っています。

あわせて読みたい

【数学史3-3】バビロニアでは小数まで60進法！その利点と問題点は？ 2種類の楔形文字で表されるバビロニアの数字。実は、同じ楔形文字で小数も表すことができます。その表し方や問題点、そもそもなぜ60進法がこの地で好まれたのかを、この記事では解説します。

　ちなみに、一の位が縦式となったのは紀元後400年頃の話で、それ以前は一の位が横式でした。

　時代と共に、一の位の右側に算木を置いて小数点以下の位を表すことも始まり、数学の進歩に応じて算木の使い方も進化しています。

2色の算木で負の数まで表せた

　算木は赤と黒の2種類が用意され、赤い算木は正の数を、黒い算木は負の数を表すために使われました。

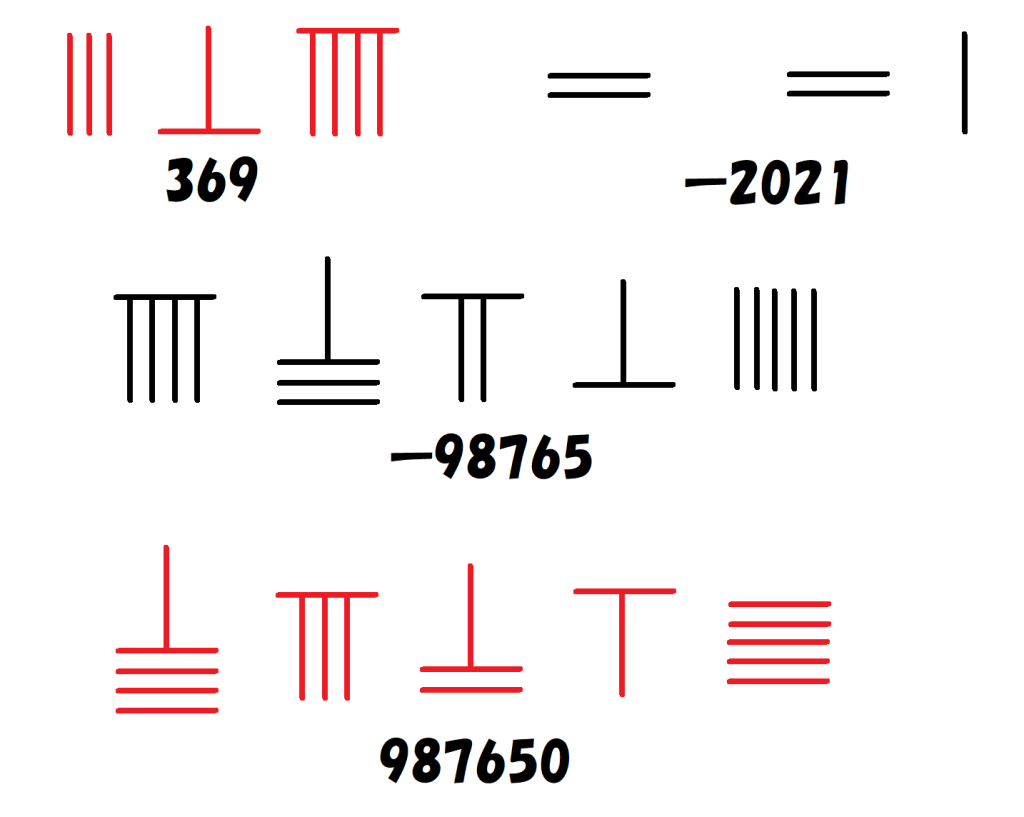
　他の国に比べ、負の数の概念をいち早く獲得していたことを証拠づけるもので、『九章算術』の中にも負の数を説明する以下の文言が登場します。

正を無入から引いて負とし、負を無入から引いて正とする

『九章算術』より

　「無入」は$~0~$を表すため、$~0~$から正の数をひくと負の数になり、$~0~$から負の数をひくと正の数になることを説明した文章だとわかります。

算木は持ち運びに不便だった

　大きな数を表したり、たくさんの計算をこなしたりするときには、大量の算木が必要になるため、持ち運びには適していませんでした。

　そこで、持ち運びに適したそろばんが開発され、中国においては13世紀以降に広く使われるようになります。

　古代ギリシャや古代ローマの時代のアバクスが、そろばんの前身ではあるものの、$~5~$本で棒の向きが変わる算木がそろばんの開発に大きな影響を与えたと言えるでしょう。

算木による計算方法

　紀元前2世紀頃から明時代（1368～1644）まで、算木は計算を素早く行うために使われていました。

　計算の基本であるたし算やかけ算はどのように行っていたのでしょうか？

たし算は同じ位どうしをたせばよい

　まずはたし算について、以下の例で説明します。

算木を用いた加法

$~27+6~$を計算する。

---

STEP

算木を置く

　1行目の十の位に$~2~$、一の位に$~7~$を置き、2行目の一の位に$~6~$を置く。

STEP

一の位を計算する

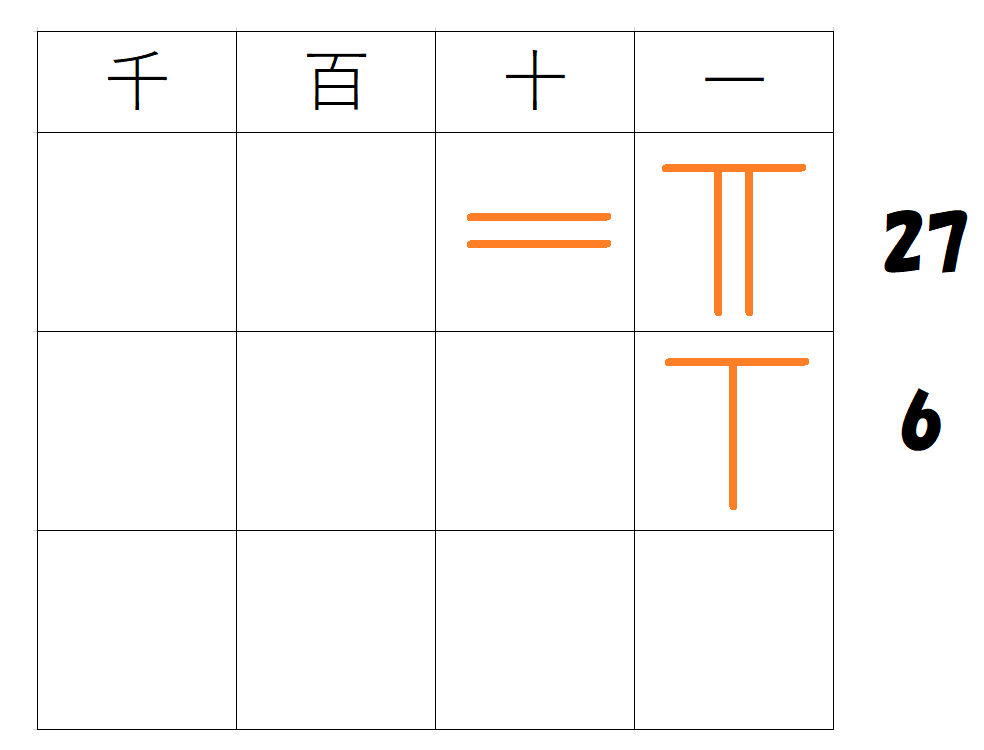
　一の位の列の$~7~$と$~6~$をたし、その和を一番下の行に配置する。
　和は$~13~$なので、十の位が$~1~$、一の位が$~3~$。

STEP

十の位を計算する

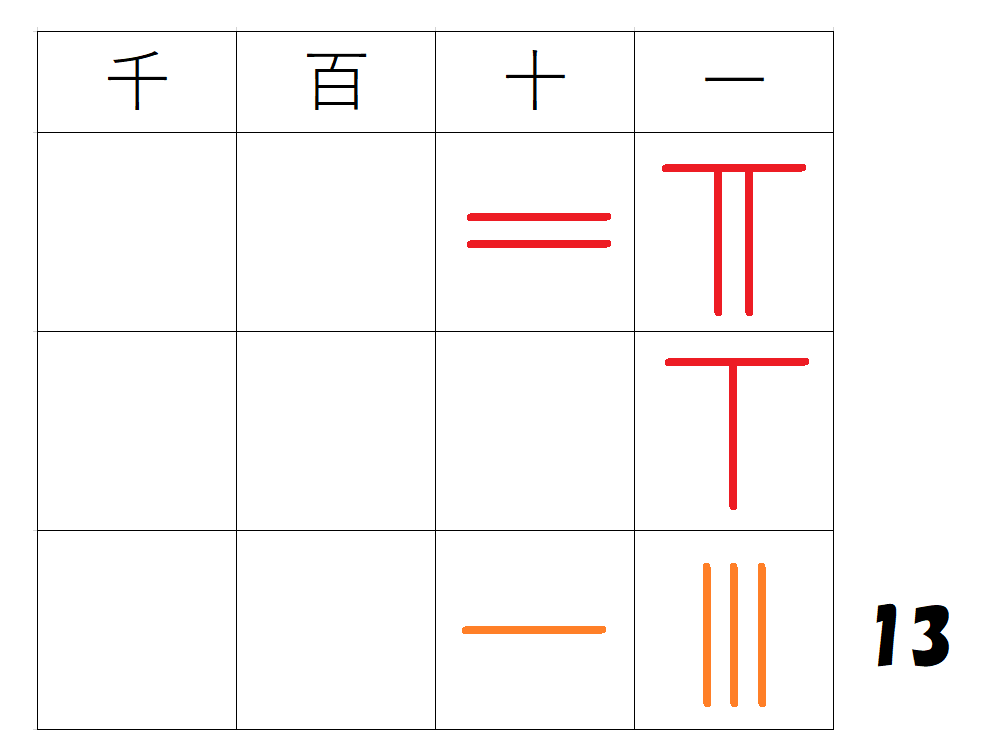
　十の位の列の$~2~$と$~1~$をたし、一番下の十の位の算木を$~3~$にする。

STEP

一番下の行から答えを読み取る

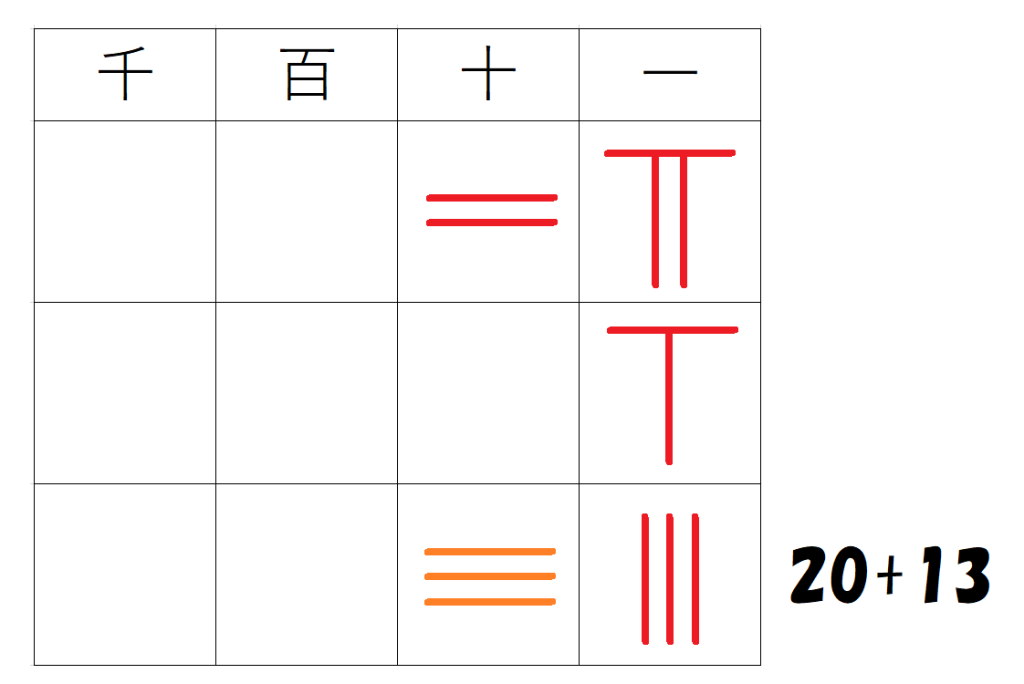
　十の位は$~3~$、一の位も$~3~$なので、$~27+6=33~$とわかる。

　繰り上がりの考え方も含め、今の筆算と同じ原理で算木を動かしていることがわかります。

　ちなみに、出てきた答えは漢数字を使って、紙に記録されました。

あわせて読みたい

【数学史5-2】甲骨文字で数字はどう表す？現在の漢数字ができるまでの流れまで解説！ 紀元前16世紀頃の殷時代に使われた甲骨文字。数字も用意されており、基本の13種類の数字とそれらを組み合わせた合字によって、様々な数を表していました。この記事では、その数の表し方を解説すると共に、どのような流れで現在の漢数字（楷書体）へと文字が変化していったのかを辿ります。

かけ算は位取りが重要

　かけ算は、算木を置く場所が重要になってきます。

算木を用いた乗法

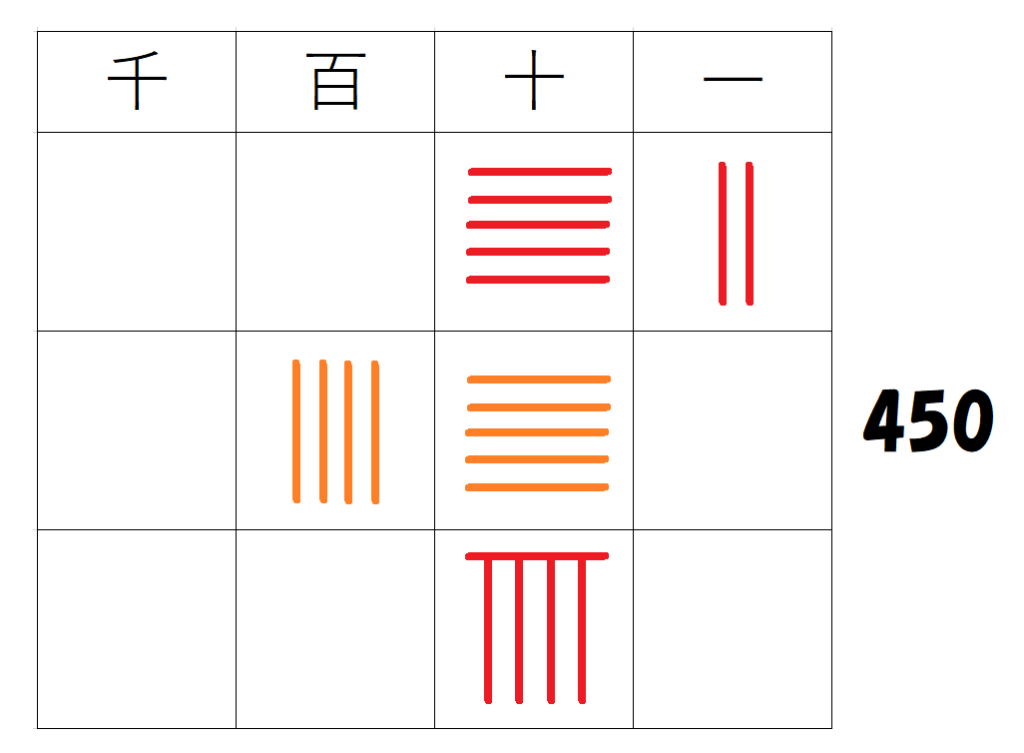
$~52 \times 9~$を計算する。

---

STEP

算木を置く

　1行目の十の位に$~5~$、一の位に$~2~$を置き、3行目の十の位に$~9~$を置く。
（$~52~$の最高位である十の位に合わせる）

STEP

十の位を計算する

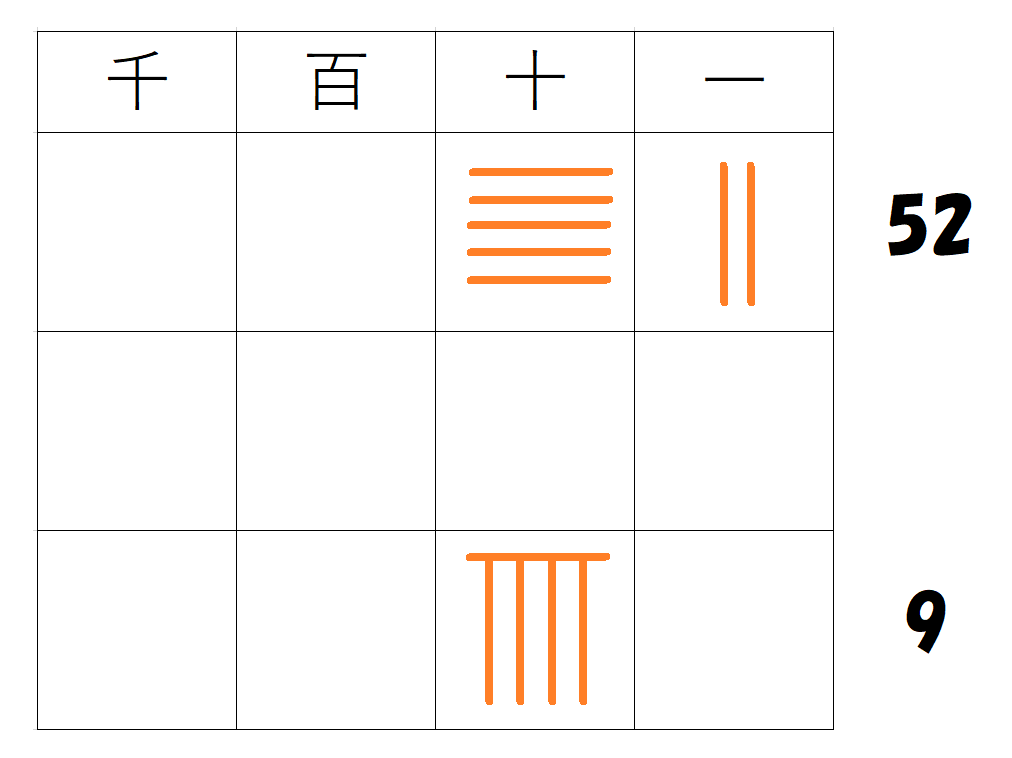
　十の位の列の$~5~$と$~9~$をかけ、その積$~45~$を真ん中の行に配置する。
　ただし、十の位を右端とするため、百の位が$~4~$、十の位が$~5~$。

STEP

かける数の位を移動する

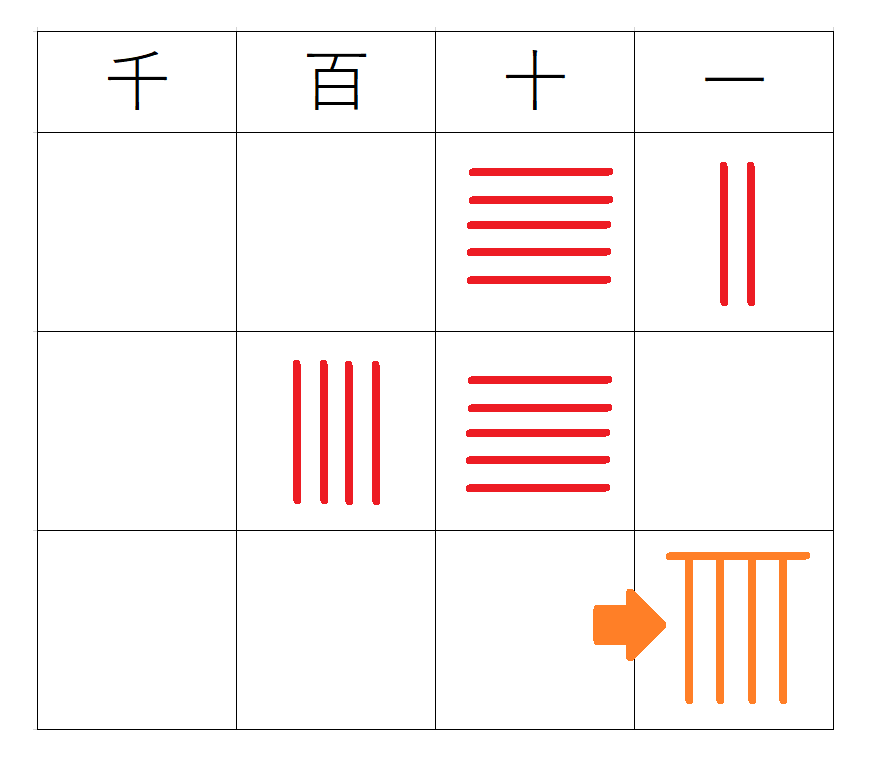
　かける数である$~9~$を、一の位へ移動する。

STEP

一の位を計算する

　一の位の列の$~2~$と$~9~$をかけ、その積$~18~$を真ん中の行にたす。

　百の位は$~4~$のまま、一の位は$~8~$、十の位は$~5~$と$~1~$をたして$~6~$。　

STEP

真ん中の行から答えを読み取る

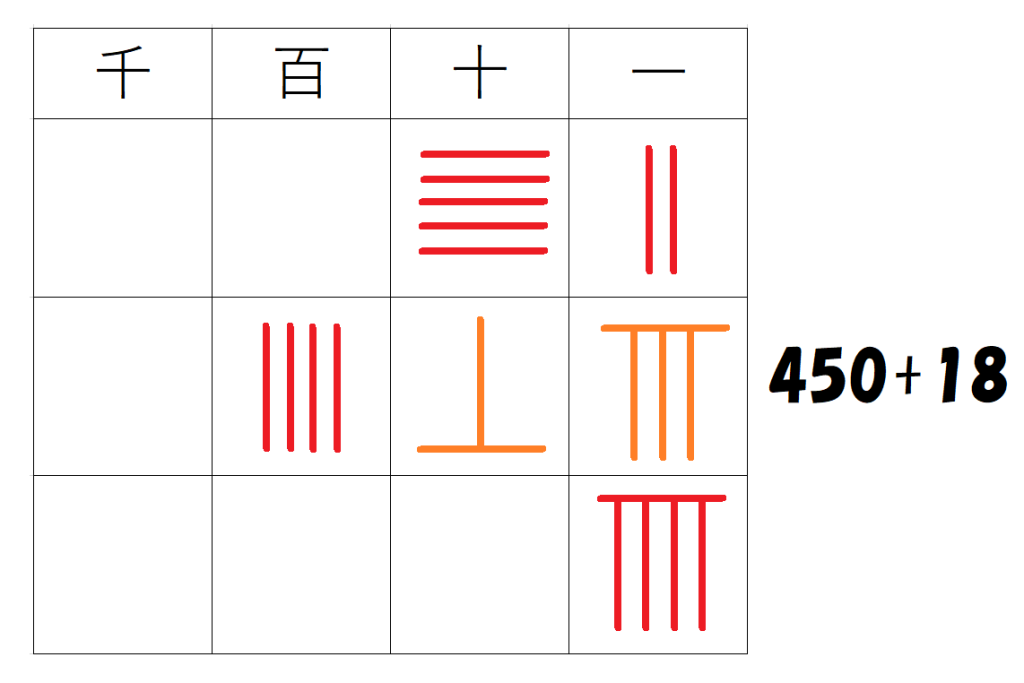
　百の位から$~4~,~6~,~8~$なので、$~52+9=468~$とわかる。

　算木によるかけ算は、分配法則に基づいています。

\begin{align*}
52 \times 9&=(50+2) \times 9  \\
&=450+18  \\
&=468
\end{align*}

　かけ算では算木を複雑に動かしましたが、当時の役人はものすごいスピードで行っていたようです。

　「算木は飛ぶように見え、その動きがあまりにも速いので目で追うことができないほどである」と11世紀の著述家は描写しています。

まとめ・参考文献

　古代中国から使われていた算木の歴史とその使い方について解説しました。

• 紀元前2世紀頃から明の時代まで算木で計算が行われた。
• 2色の算木を用いることで、正の数と負の数を表した。
• 計算に使用する際には、同じ位の数字どうしで、算木を動かした。

　紀元前から負の数を扱っていた中国。
　次の記事では、古代中国の方程式について解説します。

次の記事へ

【数学史5-4】『九章算術』の連立方程式は歴史的にも高レベル！行列を使った解法を解説！ 　紀元前2世紀頃にでき、中国数学を体系立てた数学書である『九章算術』。その7,8章には、連立方程式の解法が載っており、解を仮定する「盈不足」と、行列の掃き出し法のもとになった「方程術」の2つが扱われていました。この記事では、それらの解き方を解説すると共に、『九章算術』に載っていた負の数の概念についても紹介します。

この章のまとめへ

【数学史まとめ5】古代中国の数学 　四大文明の一つで長い歴史を持つ中国。 　しかし、紀元前213年の焚書政策により、紀元前の数学関係の資料はほとんど失われてしまいました。 　そのため、古代中国の数…

　横式の$~1~$から$~4~$、甲骨文字の$~1~$から$~4~$と似ているね。

それもそのはず。算木を並べた形をそのまま文字にしたからだよ。