【数学史２－６】リンド・パピルスの有名問題を解説！方程式は仮置法で解ける！

　古代エジプトの数学を、現代にまで伝える役割を果たしたパピルス。

　そのパピルスの中でも最も有名なのが、紀元前1650年頃に書記アーメスが書いた『リンド・パピルス』です。

　その『リンド・パピルス』では、パンの分け方や土地の面積などの実用的な数学の問題だけでなく、生活とは直接結びつかない方程式や数列の問題まで載っていました。

　この記事では、古代エジプトにおける方程式の解き方をはじめ、『リンド・パピルス』に載っている有名な問題を解説していきます。

『リンド・パピルス』に載っている方程式

　『リンド・パピルス』は、紀元前1650年頃に古代エジプトの書記アーメスによって書かれた巻物で、実生活につながる問題を中心に、幅広い分野の問題が80以上載っています。

　古代エジプトの数学の特徴は、実用的な面を重んじるところにありましたが、その中で異彩を放つのが方程式の問題です。

方程式は「アハ問題」と呼ばれた

　現代の方程式にあたる問題は、「アハ問題」と呼ばれました。
　その理由は、問題文にあります。

　「アハ」というのは、量を意味する言葉で、今で言う未知数$~x~$にあたります。

　この種の問題は、文頭が「アハ」で始まるため、「アハ問題」と名付けられました。

　ちなみに、パンの分け方や円形の土地の面積の求め方といった実用的な面での数学がメインだった古代エジプトでは、「アハ問題」は珍しい種類の問題だったのです。

アハ問題は「仮置法」で解いた

　方程式の問題は、現在であれば移項や等式の性質を用いて簡単に解くことができます。

　しかし、古代エジプトでは「仮置法」と呼ばれる、比例の考え方の応用で解いていました。

　先ほどの『リンド・パピルス』問題26を「仮置法」で解くと、以下のようになります。（表記方法は現代の方法）

x+\frac{1}{4}x=15

4+\frac{1}{4}\times 4=5 ~~~\cdots ①

4 \times 3 +\frac{1}{4}\times 4 \times 3=15

　このように、$~x~$に何か適当な数を代入し、そこから得られた値と得たい値の比例関係から$~x~$を求める方法が「仮置法」です。

　この方法のすごいところは、どんな値を代入しても比例関係を使って必ず解けるところです。

実際の計算量は膨大

　『リンド・パピルス』には、いくつかアハ問題が載っていました。

　例として、以下の2問を見てみましょう。　

　実はこれらの問題、答えが非常に複雑で、問24は現在の表記で$~\displaystyle \frac{133}{8}~$、問31は、$~\displaystyle \frac{1386}{97}~$が「アハ」の値となります。

　しかも、当時のかけ算・わり算は「２倍法」を利用し、分数は単位分数の和で表していたので、実際の「アハ」の値は、

 \frac{133}{8}=16+\frac{1}{2}+\frac{1}{8}

 \frac{1386}{97}=14+\frac{1}{4}+\frac{1}{56}+\frac{1}{97}+\frac{1}{194}+\frac{1}{388}+\frac{1}{679}+\frac{1}{776}

というように表されていました。

　『リンド・パピルス』の著者であるアーメスの計算力の高さが窺えます。

アーメスは検算もしていた

　書記アーメスは、アハ問題を解くだけでなく、求まった「アハ」の値が正しいかを代入して確かめています。

　今で言うところの「検算」をしていたということです。

　検算という行為は、後の古代ギリシャで登場する証明にもつながる考え方であると同時に、どんな複雑な問題も仮置法によって解けるという自信の表れにもなっています。

ピラミッドの勾配は計算されていた

　古代エジプトと言えば、ピラミッド。

　ピラミッドを建造するにあたって、外壁の勾配を均一にすることが重要でした。

水平距離と高さにはそれぞれ別の単位が使用された

　水平距離には、手のひらの幅を意味する「パーム」という単位が使われていました。

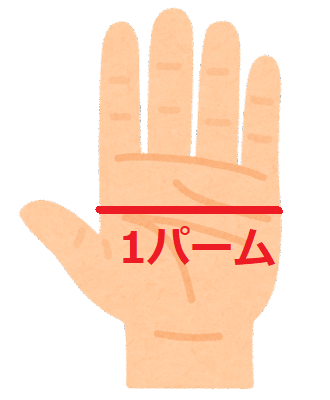
　現在では、

1パーム=7.62 ~cm

とされています。

　高さの単位は「キュービット」が使われており、中指の先から肘までの長さを意味していました。

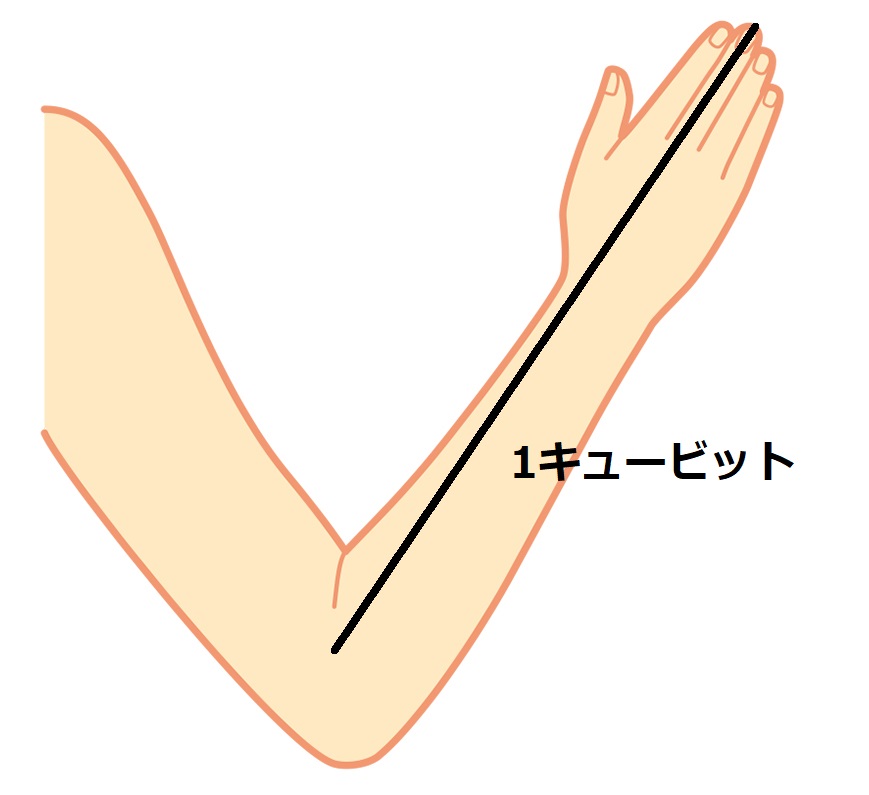
　地域や時代によって長さが異なるものの、古代エジプトにおいては、

1キュービット\fallingdotseq52.4 ~cm

であり、パームの約 7 倍の長さを示していました。

勾配は cot（コタンジェント）で表した

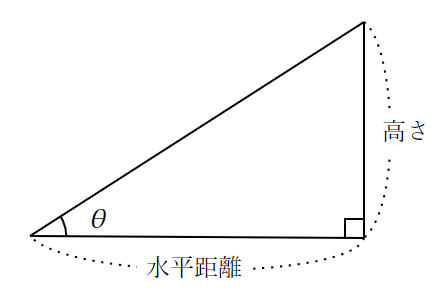
　勾配を表す数値として、古代エジプトでは「セケド」と呼ばれる、高さ１キュービットあたりの水平距離（パーム）を使っていました。

セケド=\frac{水平距離(パーム)}{高さ(キュービット)}=\cot{\theta}

　これは、現在で言うところの$~\cot{}~$（コタンジェント、余接）であり、$~\tan{}~$の逆数です。

　この時代から三角比の考え方があったことがわかります。

『リンド・パピルス』のピラミッドの問題

　『リンド・パピルス』に載っている、ピラミッドの勾配に関する問題は次のようなものでした。

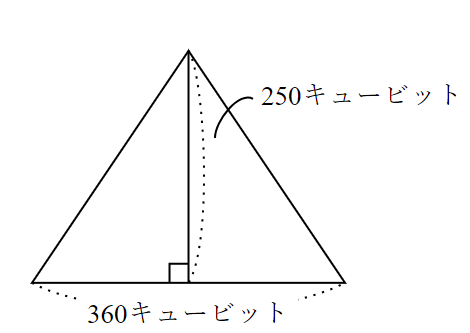
　この問題に対する、書記アーメスの解法がこちら。

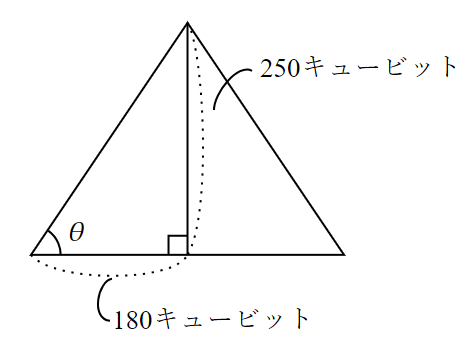
　単位分数で表しているという点を除けば、

\cot{\theta}=\frac{180}{250}=\frac{18}{25}

の計算をしているだけです。

　最後の$~7~$倍は、m（メートル）をcm（センチメートル）に直すような単位換算なので、惑わされないようにしましょう。

　$~\cot{}~$だから馴染みがないものの、$~\tan{}~$の逆数を紀元前から使っていたと考えると、当時のエジプト人の頭脳に驚かされます。

クフ王の大ピラミッドとほぼ同じ勾配

　一番大きなクフ王のピラミッドは、幅が$~440~$キュービット、高さが$~280~$キュービットです。

　そのため、

\cot{\theta}=\frac{220}{280}=\frac{1}{2}+\frac{1}{4}+\frac{1}{28}

であり、単位をキュービットからパームに直すことで、セケドは$~5~$と$~\displaystyle \frac{1}{2}~$パームとなります。

　リンド・パピルスでのセケドが、$~5~$と$~\displaystyle \frac{1}{25}~$パーム であったため、類似度が高いことが言えるでしょう。

　リンド・パピルスができる約900年前に、クフ王のピラミッドは完成しているため、アーメスは測量をしたうえで問題を作成したと考えられます。

『モスクワ・パピルス』には体積の求め方まで記載

　ちなみに、『モスクワ・パピルス』には、ピラミッドの体積の求め方に繋がる問題もありました。

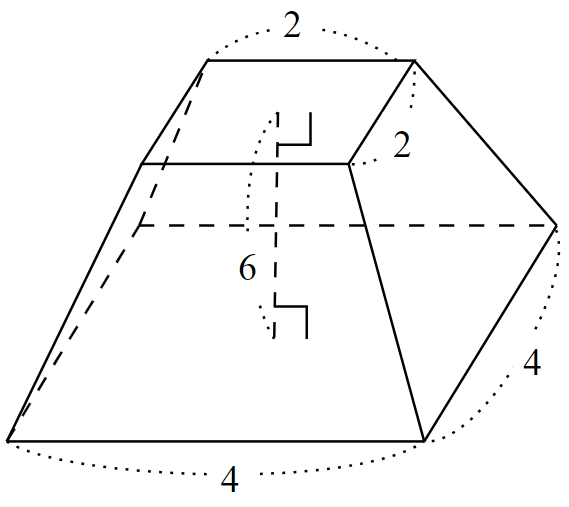
　実際はピラミッドではなく、今で言う四角錐台の体積を求める問題です。
　この体積の解法が次のように書かれています。

　この解法を、現代の数式で表すと、

(4^2+4\times 2+2^2)\times 6 \times \frac{1}{3}=56

であり、底面と頂面の正方形の一辺をそれぞれ$~a~,~b~$、高さを$~h~$としたときの四角錐台の体積が

\frac{h}{3}(a^2+ab+b^2)

で求まることを知っていた証拠になっています。

　この式で、$~b=0~$（頂面なし）とすれば、実際のピラミッドの体積も求めることができ、建設時に利用していたのではないかと推測されています。
 
　ただ、どのようにこの公式が導かれたのかは明らかになっていません。

わらべ歌として知られている数列の問題

　最後は英語圏のわらべ歌として、よく知られている『リンド・パピルス』の問題です。

『リンド・パピルス』の数列の問題

※スペルト小麦は、現在の小麦の原種にあたる穀物。
※ヘカトは、体積を表すエジプトの単位。

　答えとしては、等比数列の和ということで、

7+7^2+7^3+7^4+7^5=19607

と求まります。

童謡『マザーグース』に登場するわらべ歌の先祖

　日本語でも「ロンドン橋落ちた」や「メリーさんのひつじ」で知られる童謡『マザーグース』。

　その中に『As I was going to St Ives』（セント・アイヴスに行く途中）というなぞなぞ歌があります。

As I was going to St Ives,

I met a man with seven wives,

Each wife had seven sacks,

Each sack had seven cats,

Each cat had seven kits:

Kits, cats, sacks, and wives,

How many were there going to St Ives?

Wikipedia「As I was going to St Ives」 より

　この歌詞を日本語にすると、次のようななぞなぞとなります。

　表現こそ違いますが、『リンド・パピルス』問題79に通じるものがありますね。

　このなぞなぞの答えは、$~1+7+7^2+7^3+7^4=2801~$に自分を入れて$~2802~$人でしょうか？

　いいえ、「セント・アイヴスに行く途中」に、妻を連れた男に会っているので、実際にセント・アイヴスに向かっているのは自分一人だけです。
　みなさんは正解しましたか？

　YouTubeで調べると、動画も出てきます↓