三角錐数は三角数を重ねた数列！その一般項や美しい性質を解説！

　数学の魅力的な世界には、様々な数列が存在します。

　その中の1つである「三角錐数」は、三角数を積み重ねて形成される数列であり、その形状が三角錐を連想させます。

　この記事では、三角錐数の一般項の導出方法や、その独特な性質や数学的な魅力について解説！

　三角錐数の第22項は2024なので、大学受験や定期テストで出てくるかもしれません。

三角錐数とは何か？

　まずは、三角錐数がどんな数列なのかを見てみましょう。

三角錐数の定義

　三角錐数は、三角数や正方形数などと同様に、ある規則に従って玉や石を置いた時の形から定義されます。

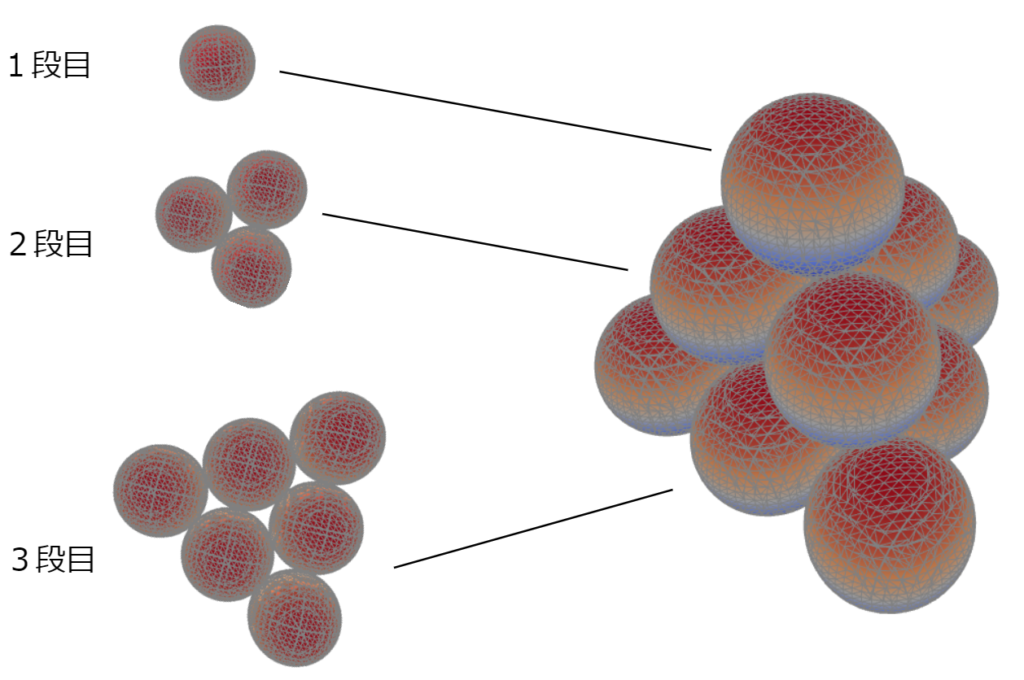
　三角錐数の第3項までを図にすると、以下のようになります。

　三角錐の中でも全ての面が正三角形なので、正四面体数とも呼ばれます。

三角数との関係

　三角錐数は、紀元前6世紀のピタゴラスが定義した三角数と密接な関係があります。

　3つめの三角錐数で考えると、上から1段目が$~1~$、2段目が$~3~$、3段目が$~6~$となっているのがわかるでしょう。

　数字で三角数と三角錐数を整理すると、以下のような表でまとめられます。

　図3や表4からもわかる通り、$~n~$番目の三角錐数は、

• $~1~$番目から$~n~$番目までの三角数の和
• $~n-1~$番目の三角錐数と$~n~$番目の三角数の和

として表すことができます。

三角錐数の一般項とその求め方

　三角錐数$~a_n~$は次のような式で求められます。

a_n=\frac{n(n+1)(n+2)}{6}

　この求め方を、先ほどの三角数$~\left(~\displaystyle b_n=\frac{n(n+1)}{2}~\right)~$との関係2通りから導いてみましょう。

①　n番目までの三角数の和で表せる

　三角錐数は三角数をどんどん重ねていった数列でした。

　そのため、$~1~$番目から$~n~$番目までの三角数の和で表すことができます。

\begin{align*}
a_n&=\sum_{k=1}^{n} b_k  \\
\\
&=\sum_{k=1}^{n} \frac{k(k+1)}{2}  \\
\\
&=\frac{1}{2}\sum_{k=1}^{n}(k^2+k)  \\
\\
&=\frac{1}{2}\left\{ \frac{n(n+1)(2n+1)}{6}+\frac{n(n+1)}{2}   \right\}  \\
\\
&=\frac{n(n+1)}{12}\left\{ (2n+1)+3   \right\}  \\
\\
&=\frac{n(n+1)}{12}( 2n+4)  \\
\\
&=\frac{n(n+1)(n+2)}{6}  \\
\end{align*}

　 和の記号$~\sum~$の良い計算問題になりそうですね。

②　n-1番目の三角錐数とn番目の三角数の和

　既存の$~n-1~$番目の三角錐数に、新たに$~n~$番目の三角数を追加することで、$~n~番目の三角錐数を作ることができます。

a_n=a_{n-1}+b_n

a_{n+1}=a_{n}+b_{n+1}

\begin{align*}
a_{n+1}&=a_{n}+\frac{(n+1)\{(n+1)+1\}}{2}  \\
\\
&=a_{n}+\frac{(n+1)(n+2)}{2}  \\
\end{align*}

\begin{align*}
a_n&=a_1+\sum_{k=1}^{n-1} \frac{(k+1)(k+2)}{2}  \\
\\
&=1+\frac{1}{2}\sum_{k=1}^{n-1}(k^2+3k+2)  \\
\\
&=1+\frac{1}{2}\left\{ \frac{(n-1)n(2n-1)}{6}+\frac{3(n-1)n}{2} +2(n-1)  \right\}  \\
\\
&=\frac{12}{12}+\frac{1}{12}\left\{n(n-1)(2n-1)+9n(n-1)+12(n-1)  \right\}  \\
\\
&=\frac{12+2n^3-3n^2+n+9n^2-9n+12n-12}{12}  \\
\\
&=\frac{2n^3+6n^2+4n}{12}  \\
\\
&=\frac{n^3+3n^2+2n}{6}  \\
\\
&=\frac{n(n^2+3n+2)}{6}  \\
\\
&=\frac{n(n+1)(n+2)}{6}  \\
\end{align*}

\frac{1(1+1)(1+2)}{6}=1 

a_n=\frac{n(n+1)(n+2)}{6} 

　 階差数列型なので、計算や手続きが面倒。

　①三角数の和として求めた方がシンプルでわかりやすいでしょう。

あわせて読みたい

【階差数列型の疑問】n=1 の確かめは必要？　成り立たない例はあるのか？ 階差数列を利用する数列の問題では、Σを使った計算結果が、n=1でも成り立つかどうかを最後に確かめます。なぜこれが必要なのか？　また、n=1で成り立たない例はあるのかを解説します。

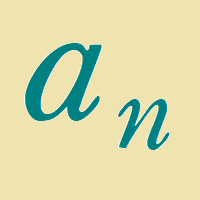
奇数番目の三角錐数の性質

　奇数番目の三角錐数$~1~,~10~,~35~,~84~,~\cdots~$に共通する性質の紹介です。

奇数番目の三角錐数は奇数の平方和で表せる

　そのシンプルさが美しい性質です。

　実際に三角錐数の第1項、第3項、第5項、第7項を見てみましょう。

\begin{align*}
a_1&=1=1^2  \\
a_3&=10=1^2+3^2  \\
a_5&=35=1^2+3^2+5^2  \\
a_7&=84=1^2+3^2+5^2+7^2
\end{align*}

　一般化すると、

$~2k-1~番目の三角錐数（奇数で$~k~$番目）は、$~k~$番目までの奇数の平方和で表せる。

ということになります。

Σ によって証明ができる

　求めたいのは次の等式。

a_{2k-1}=\sum_{\ell=1}^{k}(2\ell-1)^2

　右辺を式変形していくことで、証明をすることができます。

\begin{align*}
\sum_{\ell=1}^{k}(2\ell-1)^2&=\sum_{\ell=1}^{k}(4\ell^2-4\ell+1)  \\
\\
&=\frac{4k(k+1)(2k+1)}{6}-\frac{4k(k+1)}{2}+k  \\
\\
&=\frac{8k^3+12k^2+4k-12k(k+1)+6k}{6}  \\  
\\
&=\frac{8k^3+12k^2+4k-12k^2-12k+6k}{3}  \\  
\\
&=\frac{8k^3-2k}{3}  \\  
\\
&=\frac{2k(4k^2-1)}{3}  \\  
\\
&=\frac{(2k-1)(2k)(2k+1)}{6}  \\
\\
&=a_{2k-1}

\end{align*}

　$~\displaystyle \sum~$が登場する恒等式の証明は、$~\displaystyle \sum~$側から式変形をしていくと計算しやすいです。

偶数番目の三角錐数の性質

　偶数番目の三角錐数$~4~,~20~,~56~,~120~,~\cdots~$に共通する性質の紹介です。

偶数番目の三角錐数は偶数の平方和で表せる

　奇数のときと同様の性質です。
　偶数のときにも同様に成り立っているのが美しさを際立たせています。

　実際に三角錐数の第2項、第4項、第6項、第8項を見てみましょう。

\begin{align*}
&a_2=4=2^2  \\
&a_4=20=2^2+4^2  \\
&a_6=56=2^2+4^2+6^2  \\
&a_8=120=2^2+4^2+6^2+8^2
\end{align*}

　一般化すると、

$~2k~番目の三角錐数（偶数で$~k~$番目）は、$~k~$番目までの偶数の平方和で表せる。

ということになります。

こちらも Σ によって証明ができる

　求めたいのは次の等式。

a_{2k}=\sum_{\ell=1}^{k}(2\ell)^2

　こちらも、右辺を式変形していくことで、証明をすることができます。

\begin{align*}
\sum_{\ell=1}^{k}(2\ell)^2&=\sum_{\ell=1}^{k}(4\ell^2)  \\
\\
&=\frac{4k(k+1)(2k+1)}{6}  \\
\\
&=\frac{2k(2k+2)(2k+1)}{6}  \\
\\
&=\frac{(2k)(2k+1)(2k+2)}{6}  \\
\\
&=a_{2k}

\end{align*}

　偶数のほうが式変形がしやすいですね。

　この性質を利用すると、三角錐数の第22項である$~2024~$は、次のように変形できます。

2024=2^2+4^2+6^2+\cdots+22^2

あわせて読みたい

2024はどんな数字？素因数分解や約数、2024を含む数列を解説！ 2024ってどんな数？2024は何で割れるの？という疑問に答えます！実は、2024は 2-0+2-4=0 より 11 の倍数です！ また、2024は婚約数や三角錐数、ハーシャッド数であり、これらの数の性質についてわかりやすく解説しています。

パスカルの三角形にも三角錐数が登場する

　最後におまけ。

　フランスのブレーズ・パスカル（Blaise Pascal , 1623～1662）が研究した「パスカルの三角形」の中にも、三角錐数が登場します。

　パスカルの三角形の4段目の$~1~$を起点に、ななめに三角錐数が現れているのがわかるでしょう。

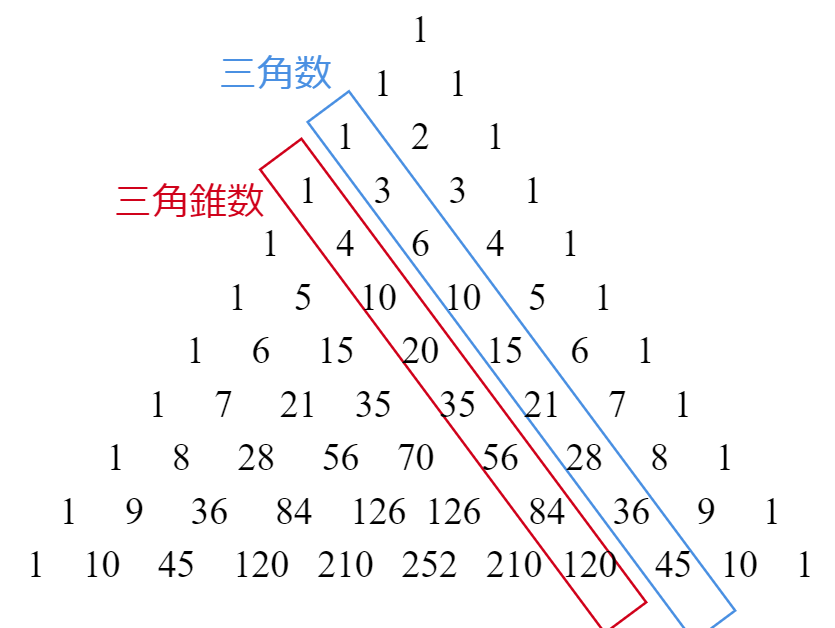
　パスカルの三角形の作り方と、$~n~$番目の三角錐が$~n-1~$番目の三角錐数と$~n~$番目の三角数の和で作られることが一致しているため、このように三角錐数が出てくるのです。

　1654年、整数論が好きだったピエール・ド・フェルマー（Pierre De Fermat , 1607～1665）が、三角数がパスカルの三角形に登場することをパスカルに手紙で伝えて数論に誘おうとしたものの、パスカルはスルーしたという歴史もあります。

フェルマー

パスカル君、君の三角形では三角数が出てくるよ。面白いよね～。
一緒に数論やろう！

パスカル

僕は興味ないなぁ。最近のマイブームは幾何学や神学。
読まなかったことにしよう。

　フェルマーは三角錐数の存在には気づいていたのでしょうか‥‥。

まとめ

　三角錐数（正四面体数）の性質について詳しく見てきました。

• 三角錐数は、三角数をたしていった数列である。
• 奇数の三角錐数は、奇数の平方和で表せる。（偶数も同様）
• パスカルの三角形の中にも三角錐数が現れる。

　$~2024~$が第22項に登場するため、$~2024~$年実施の入試や定期テストで関連した問題が出てくるのではないでしょうか？

　数学Bの定期テストや大学入試に備えて、$~\displaystyle \sum~$の復習をしておきましょう。

奇数には奇数（の平方和）を。偶数には偶数（の平方和）を。

ハンムラビ法典みたい‥‥。