2024はどんな数字？素因数分解や約数、2024を含む数列を解説！

　数学好きや受験生必見！
　2024年に向け、2024についての性質を当たり前のものからマニアックなものまでを紹介した記事です。

　毎年、西暦を使った数学ネタを年賀状にしている現役数学教員が解説！

　実は、$~2024~$は$~11~$で割りきれるだけでなく、ある珍しい性質も持っているんです。

　2024に絡めた問題は、中学入試、高校入試、大学入試などでも出題されるため、この記事を読んでおくだけでも受験対策になるかもしれません!?

2024を素因数分解してわかること

　まずは、$~2024~$の素因数分解から。

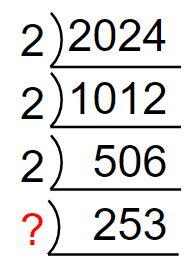
　実際にやってみると、以上のように詰まってしまうのではないでしょうか？

　実は、$~2024~$を素因数分解すると、次のようになります。

2024=2^3 \times 11 \times 23

　この式の求め方について、詳しく見てみましょう。

2024は11の倍数である

　素因数分解の結果からもわかるように、$~2024~$は$~11~$で割れます。

　素因数分解の途中で出てくる$~253~$を実際に$~11~$で割ってみればわかりますが、以下のような11の倍数判定法を使うこともできます。

　この判定法に基づき、$~2024~$の各ケタの数字を交互に加減すると、

2-0+2-4=0

となり、$~0~$は11の倍数なので$~2024~$も11の倍数とわかります。

　$~0=11×0~$だから、11の倍数。$~0~$はすべての自然数の倍数だよ。

　$~253~$で同じ判定法を用いても、

2-5+3=0

であり、$~253~$も11の倍数であることがわかります。

11の倍数判定法は前年（2023年）の7の倍数の判定法よりも簡単だね。

あわせて読みたい

倍数判定法～7の倍数や11の倍数にも見分け方はある!?　証明含めて様々な倍数判定法を解説～ 2の倍数かどうかは下1桁で、3の倍数かどうかは各桁の和でわかりますが、7の倍数や11の倍数はどう判定するのでしょうか？ 各判定法の証明や必ず覚えるべきものを現役数学教員が解説。必要な判定法を覚えて、約分や素因数分解を効率的に行えるようになりましょう。

2024のテクニカルな素因数分解

　翌年の$~2025~$が$~45^2~$であることを知っていれば、次のような式変形から素因数分解することが可能です。

\begin{align*}
2024&=2025-1  \\
&=45^2−1^2\\
&=(45+1)×(45-1)\\
&=46×44\\
&=(2×23)×(2^2×11)  \\
&=2^3 \times 11 \times 23
\end{align*}

　中3 で習う因数分解公式$~a^2-b^2=(a+b)(a-b)~$を利用しているよ。

　　実は$~45^2~$は瞬時に計算できるので、意外と気付いた人も多いのではないでしょうか？

いや、普通気づけないって。

あわせて読みたい

一の位が5である自然数の2乗は暗算できる！証明までわかりやすく解説！ 　$~5^2~$,$~15^2~$,$~25^2~$,‥‥$~95^2~$などの一の位が$~5~$である自然数の2乗は、非常に簡単に計算することができます。 　実は、十の位が$~a~$、一の位が$~5~$である…

2024の約数は16個で総和は4320

　素因数分解の結果から、$~2024~$の約数について以下のことがわかります。

(3+1)\times (1+1)\times(1+1)=16~(個)

\begin{align*}
&~~~~(1+2^1+2^2+2^3)(1+11^1)(1+23^1)   \\
&=15 \times 12 \times 24  \\
&=4320
\end{align*}

　具体的に、2024の約数を小さい順に並べてみると、$~1~$,$~2~$,$~4~$,$~8~$,$~11~$,$~22~$,$~23~$,$~44~$,$~46~$,$~88~$,$~92~$,$~184~$,$~253~$,$~506~$,$~1012~$,$~2024~$であり、自身（$2024$）を除く約数の和は$~2296~$となるため、$~2024~$は過剰数（自身以外の約数の和が、自身よりも大きくなる数）と言うこともできます。

昨年は不足数でした。
不足数よりも過剰数の方がレアです。

2024は22番目の三角錐数

　紀元前6世紀の数学者ピタゴラスが定義した「三角数」。

　その派生形である三角錐数は、次のように定義されます。

　各頂点から対称な三角錐というのは正四面体のこと。
　そのため、三角錐数は「四面体数」とも呼ばれます。

　三角錐数は、次のような数列を成します。

　22段目まで積んだ三角錐に必要な球の個数が2024ということです。

　三角錐数$~a_n~$の一般項は、

\begin{align*}
a_n&=1+3+6+10+\cdots +\frac{n(n+1)}{2}  \\

&=\sum_{k=1}^n \frac{k(k+1)}{2}  \\

&=\frac{1}{6}n(n+1)(n+2) 
\end{align*} 

と表すことができるため、

2024=\frac{22\times23\times24}{6}

という美しい数式も導くことができます。

22段目までって気が遠くなるなぁ‥‥。

あわせて読みたい

三角錐数は三角数を重ねた数列！その一般項や美しい性質を解説！ この記事では、三角錐数に関する数学的概念を解説しています。三角数を基にした三角錐数の定義、それらの数の特徴、一般項の導出方法、そして奇数番目と偶数番目の三角錐数の異なる性質について紹介しています。また、パスカルの三角形と三角錐数の関連性にも触れられており、数学の興味深い側面を探求する内容となっています。

2024は5組目の婚約数

　2024についての性質で一番珍しいのが婚約数。

　こちらはピタゴラスが定義した「友愛数」の派生版です。

　比較のために友愛数と婚約数の定義を並べてみましょう。

　婚約数は、約数$~1~$をカウントしないバージョンの友愛数であると言えます。

　友愛数と婚約数の最初の5組を挙げると、次のようになります。

　婚約数は友愛数よりもペアが多いとされていますが、非常に珍しい数の組み合わせであることに変わりありません。

　表5の通り、肝心の$~2024~$は5番目の婚約数にあたります。

「友愛数」ではなくて、「結婚数」とかであれば「婚約数」と関連性があったのになぁ。

2024は409番目のハーシャッド数

　$~2024~$は409番目のハーシャッド数（harshad  number）です。　

　ハーシャッド数の定義は次のように与えられます。

　$~2021~$と$~2024~$を例にハーシャッド数かどうかを判別してみましょう。

　$~2022~,~2023~,~2024~,~2025~$は連続したハーシャッド数になります。（そんなに珍しくはない性質ですが‥‥）

$~2024~$が409番目という時点で、約$~\displaystyle \frac{1}{5}~$の自然数がハーシャッド数であるとわかりますね。

2024が出てくる美しい数式

　特定の名前が付いているわけではないものの、規則的で美しいと思えるような$~2024~$を含む数式を3つ紹介します。

2024は連続する自然数の立方和で表せる

　連続する自然数の3乗を使って、$~2024~$を算出することができます。

2^3+3^3+4^3+\cdots+8^3+9^3=2024

　電卓をたたいて確かめることもできますし、下のように$~\Sigma~$で計算することも可能です。

\begin{align*}
\sum_{k=2}^{9}k^3&=\sum_{k=1}^{9}k^3-\sum_{k=1}^{1}k^3  \\
\\
&=
\left( \frac{9\cdot 10}{2} \right)^2-1^3  \\
\\
&=45^2-1  \\
&=2024
\end{align*}

2025年はもっときれいな数式ができるね。

2024は連続する偶数の平方和で表せる

　今度は連続する偶数の2乗を使って、$~2024~$を算出します。

2^2+4^2+6^2+\cdots+20^2+22^2=2024

　こちらに関しても電卓をたたいて確かめることもできますし、下のように$~\Sigma~$で計算することも可能です。

\begin{align*}
\sum_{k=1}^{11}(2k)^2&=4\sum_{k=1}^{11}k^2  \\
\\
&=4\cdot \frac{11(11+1)(2 \cdot 11+1)}{6} \\
\\
&=\frac{4 \cdot 11 \cdot 12 \cdot 23}{6} \\
\\
&=2024
\end{align*}

実は、三角錐数を偶数段で区切ったときの数列の和になっています！

49! を 2402 で割った余りは2024

　最後は、$~2~$,$~0~$,$~2~$,$~4~$を使ってできる$~2024~$です。

\{2^0+24\times(2+0+2+4)\}! \equiv 2024    \pmod{2042}

　 元ネタとしては、OEIS（オンライン整数列大辞典）のA173353 に登場する

49! \equiv 2024 \pmod{49^2+1}

という数式です。

　この数式を無理やり$~2~$,$~0~$,$~2~$,$~4~$だけで表してみました。

まとめ

　$~2024~$に関する性質を紹介しました。

• $~2024=2^3 \times 11 \times 23~$と素因数分解できる。
• $~2024~$は三角錐数や婚約数、ハーシャッド数である。
• $~2024~$は、連続する自然数の立方和や連続する偶数の平方和として表せる。

　$~2024~$年は、大変珍しい婚約数の年です。
　数学ヲタクがプロポーズするなら2024年しかない！