三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。
この記事では、その中でも中3の教科書でよく登場する2つの証明方法について、現役数学教員がわかりやすく解説します。
2つの証明に共通するのは、視覚的に理解しやすく、簡単な計算で証明できるという点。
しかも、そのうちの1つは、中世インドで最も著名な数学者バスカラが発見したものだったのです。
この記事を読んで、中学生時代に一度は見たことがある図形の持つ意味を理解しちゃいましょう!
- 教科書に最もよく登場する証明方法
- 教科書に登場するバスカラの証明方法
- インドの数学者バスカラと三平方の定理
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓

教科書に最もよく登場する証明
三平方の定理の証明と聞き、最も有名なのは次の証明です。
直角をはさむ二辺の長さが$~a~,~b~$、斜辺が$~c~$の直角三角形を4つ組み合わせて、一辺が$~a+b~$の大きな正方形を図1のように作る。
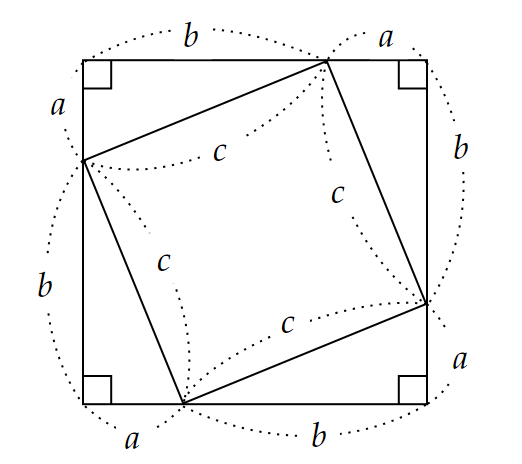
このとき、内側には一辺が$~c~$の正方形ができる。
この正方形の面積$~c^2~$は、外側の正方形の面積から、4つの直角三角形の面積を引いても求まるため、
\begin{align*}
(a+b)^2-\frac{1}{2}\cdot a \cdot b \cdot 4 &=c^2 \\
\\
a^2+2ab+b^2-2ab&=c^2 \\
\\
a^2+b^2&=c^2
\end{align*}となり、三平方の定理が示された。■
図形的にも計算的にもシンプルなことが、多くの教科書が採用している理由と言えるでしょう。
ピタゴラスの証明と最初の図は一緒で、古くからよく知られている証明法の一種です。

教科書に登場するバスカラの証明
こちらは、先ほどの証明の後の練習問題としてよく登場する証明方法です。
直角をはさむ二辺の長さが$~a~,~b~~(a < b)~$、斜辺が$~c~$の直角三角形を4つ組み合わせて、一辺が$~a+b~$の大きな正方形を図2のように作る。
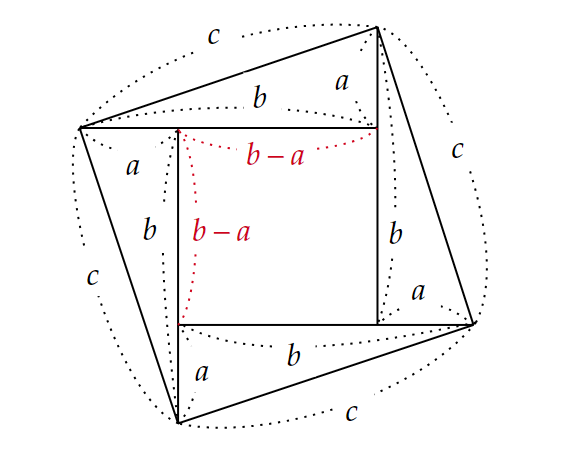
このとき、内側には一辺が$~b-a~$の正方形ができる。
一辺$~c~$の正方形の面積$~c^2~$は、一辺$~b-a~$の正方形の面積と、4つの直角三角形の面積の和でも求まるため、
\begin{align*}(b-a)^2+\frac{1}{2}\cdot a \cdot b \cdot 4 &=c^2 \\
\\
b^2-2ab+a^2+2ab&=c^2 \\
\\
a^2+b^2&=c^2
\end{align*}となり、三平方の定理が示された。■
4つの直角三角形の組み合わせ方が、三平方の定理の証明⑭と違っています。
ただ、考え方や出てくる計算の種類としては一緒なので、練習問題として選ばれている理由がわかりますね。
実は、こちらの証明を発見したのは、中世インドの大数学者バスカラでした。
バスカラと三平方の定理
インドの数学者バスカラ(Bhaskara , 1114-1185頃)は、平方根や無限大の操作を使いこなす、当時の中では卓越した才能を持つ人物です。
彼の功績の例として、以下のようなものがあります。
- 平方根には正の数だけでなく負の数も存在すると主張
- $~a \div 0=\infty~$の導入
- ペル方程式$~Dx^2 \pm 1=y^2~$の整数解の解法
バスカラの著書は何冊かあり、その中でも算術書『リーラ―ヴァ―ティー』や代数を記した『ビージャガニタ』は、教科書としてインド全体に普及したと言われています。
バスカラは 『リーラ―ヴァ―ティー』 の中で、 三平方の定理の証明⑮の図2を載せ、
 バスカラ
バスカラ見よ
とだけ述べています。
バスカラは他にも、相似を使った証明方法も発見したと言われています。


また、 バスカラの著書には、 三平方の定理の証明⑭ と 三平方の定理の証明⑮を混ぜたような図(図3)もあり、こちらの図を使った証明に関しても、



見よ
で済ませています。
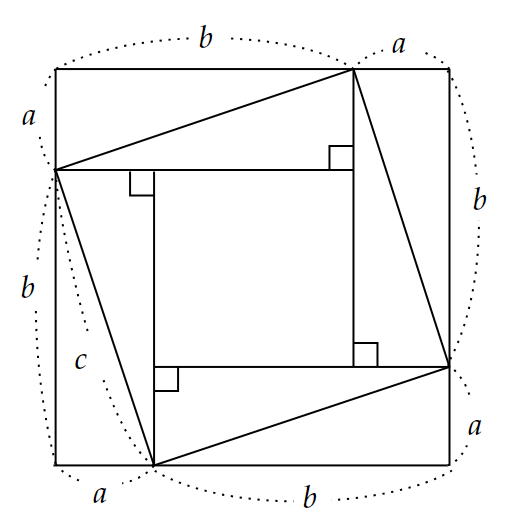

ちなみに、この図3を使った証明は、古代中国の数学書『周髀算経』にも載っていたため、歴史としては中国のほうが古いということになります。
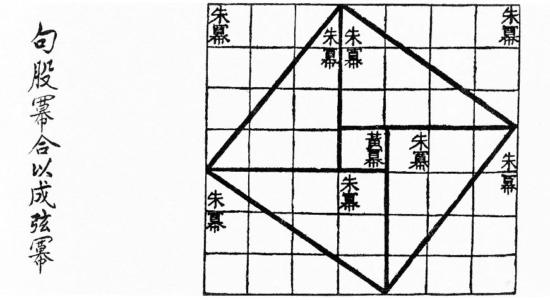

(出典:Wikimedia Commons, Public domain)
ただ、バスカラが無類の才能に恵まれ、三平方の定理の証明に精通し、インド全体の数学に影響を与えた人物であることは言えるでしょう。



それにしてもバスカラの著書は不親切だね。
証明なのに「見よ」って‥‥。



彼にとっては見ればわかるという感覚だったんだろうね。
現代日本の数学書だって、練習問題の解答が「(略)」とかになっているよ。
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓



コメント