紀元前に誕生し、中国数学の体系を完成させた『九章算術』。
『九章算術』の9章「句股」では、三平方の定理を利用した問題が多数載っていました。
その内容は、単に直角三角形の斜辺を求める問題から、植物の長さを求める問題までさまざま。
この記事では、ピタゴラス数にもつながる問題にも触れつつ、三平方の定理がどう活用されていたかを解説します。
| 時代 | B.C.2世紀頃~ |
| 場所 | 中国 |
古代中国の三平方の定理
バビロニアやインドと同様、古代中国でも、三平方の定理は知られていました。
『九章算術』9章「句股」で扱われた
紀元前2世紀頃に書かれた数学書『九章算術』。

(出典:See page for author, Public domain, via Wikimedia Commons)
その9章「句股」の問題のほとんどが三平方の定理に関するものでした。
「句」や「股」というのは直角三角形の辺の名称です。
- 「句」…長さが一番小さい辺
- 「股」…長さが2番目に小さい辺
- 「弦」…長さが一番大きい辺(斜辺)
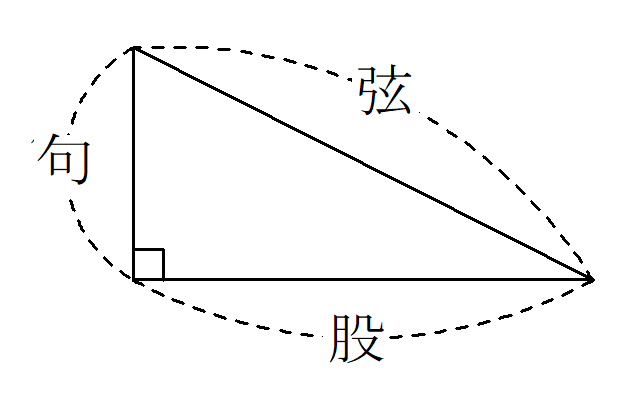
『九章算術』9章では、「句股の術」として三平方の定理が以下のように表されていました。
句・股をそれぞれ自乗※1して、それらを足して開平術を使えば、弦の長さが求まる。
股を自乗して、弦の自乗したものから引き、その余りに開平術を使えば、句の長さが求まる。
句を自乗して、弦の自乗したものから引き、その余りに開平術を使えば、股の長さが求まる。
※1 「自乗」は2乗のこと。
この「句股の術」を、辺の長さが$~a~,~b~,~c~~(a < b < c)~$の直角三角形にあてはめると、それぞれ
\begin{align*}
c&=\sqrt{a^2+b^2} \\
a&=\sqrt{c^2-b^2} \\
b&=\sqrt{c^2-a^2} \\
\end{align*}となり、確かに三平方の定理を意味していることがわかります。
9章第1問は斜辺を求めるだけの問題
『九章算術』9章の序盤は、「句股の術」(三平方の定理)を単にあてはめるだけの問題でした。
第1問は、現在の数学の教科書でも最初に出てきそうな計算問題です。
今、句が$~3~$尺※2、股が$~4~$尺の直角三角形がある。
弦の長さはいくらになるか。
※2「尺」は長さの単位で、当時は1尺=約23cmと推測されている。
この問題を図にすると、下のような最も基本的な直角三角形となります。
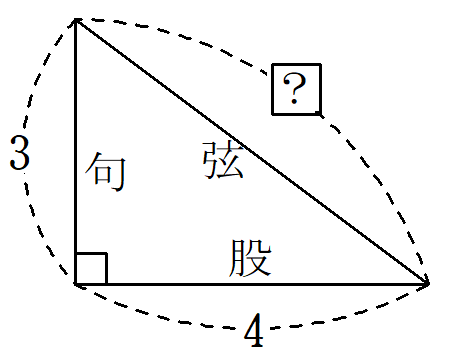
この問題に解説は無いものの、「句股の術」にあてはめるだけで、弦が$~5~$尺 と求められます。
三平方の定理の証明は『周髀算經』にある
『九章算術』には、三平方の定理の証明自体は載っていませんでした。
『九章算術』よりも古くから存在していた『周髀算經』の中で、三平方の定理の証明が図として与えられています。
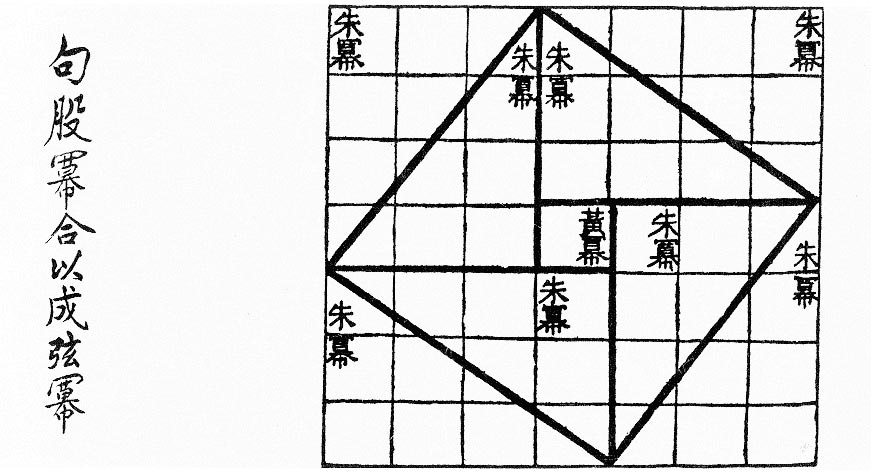
(出典:the free media repository, Public domain, via Wikimedia Commons )
この本の成立も紀元前2世紀頃と考えられており、三平方の定理を世界で初めて証明したのはピタゴラス(Pythagoras, B.C.569頃-B.C.500頃) と言われています。

(出典:The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons)
三平方の定理の文章題
現在の教科書と同じように、『九章算術』9章も単なる計算問題から始まり、文章題へと続いていきました。
池に生えている葭の長さを求める問題
文章題の例として、次の問題を見てみましょう。
池の中から顔を出している葭(植物)の長さに関する問題です。
今$~1~$丈※3四方の池があり、葭が池の中央に生えていて、水から$~1~$尺出ている。
葭を岸まで引っ張ってくると、岸とちょうど等しくなる。
水深と葭の長さはそれぞれいくらか。
※3「丈」は長さの単位で、1丈=10尺。
状況が掴みにくいですが、上から見た図と横から見た図を書くと、以下の通り。
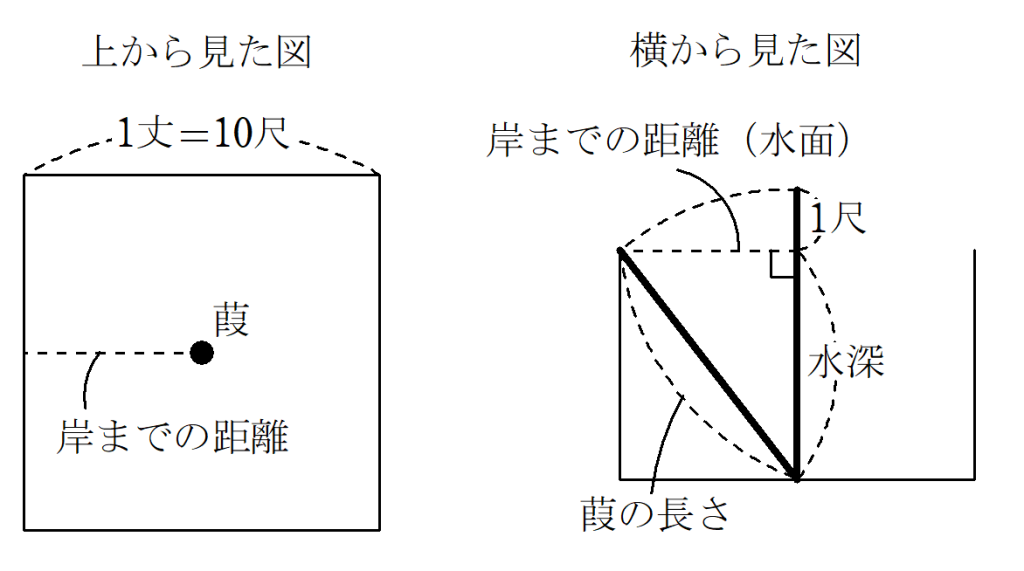
水深または葭の長さを$~x~$とすれば、三平方の定理から二次方程式ができるものの、『九章算術』における解法は特殊なものでした。
弦と股の差、句を使った公式から求めた
『九章算術』9章第6問では、以下のような専用公式(術)を使いました。
弦と股の差を$~t~$、句を$~a~$としたとき、股$~b~$と弦$~c~$は以下の式で求まる。
\begin{align*}
b&=\frac{a^2-t^2}{2t} \\
\\
c&=b+t \\
\end{align*}この問題だけでなく、他の文章題についても専用の公式が与えられており、問題文の情報をあてはめるだけで解を出しています。
今回の『九章算術』9章第6問の答えは以下のようになります。
池の正方形の一辺が$~1~$丈$~=~10~$尺なので、葭から池の端までの距離は$~5~$尺。
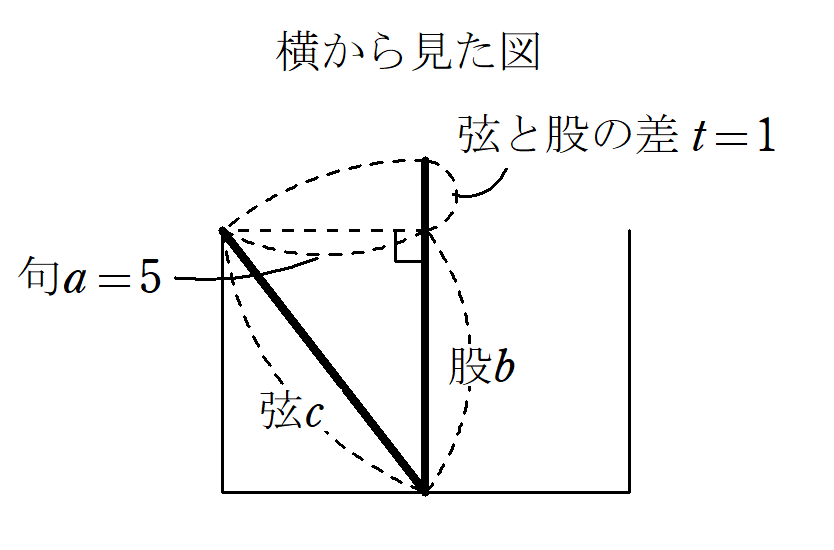
$~a=5~$と$~t=1~$を『九章算術』9章第6問の術に代入すると、
\begin{align*}
b&=\frac{5^2-1^2}{2\cdot 1} \\
\\
&=\frac{24}{2} \\
\\
&=12 \\
\\
c&=12+1 \\
&=13
\end{align*}となるため、水深$~12~$尺、葭の長さ$~13~$尺と求まる。
複雑な問題も、このように専用の公式が用意されていたため、当時はその術を暗記することで問題を解くことができました。
公式の原理は三平方の定理
『九章算術』9章第6問の術 の原理は、三平方の定理です。
現代数学を使って、証明してみましょう。
図8のように、句$~a~$、股$~b~$、弦$~c~$、股と弦の差を$~t~$とする。
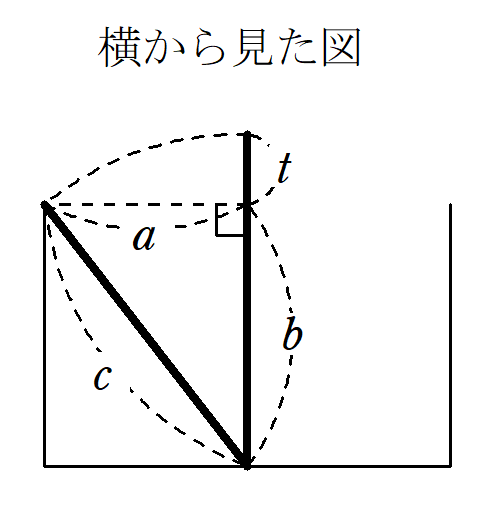
このとき、
c=b+t~~~\cdots ①
が成り立つ。
図8の直角三角形で、三平方の定理を使い、$①$を代入すると、
\begin{align*}
c^2&=a^2+b^2 \\
(b+t)^2&=a^2+b^2 \\
b^2+2bt+t^2&=a^2+b^2 \\
2bt&=a^2-t^2 \\
b&=\frac{a^2-t^2}{2t}~~~\cdots ②
\end{align*}であり、$①$と$②$より、『九章算術』9章第6問の術 が示された。
『九章算術』では、術の証明は載っていませんでした。
しかし、他の問題で複雑な公式が存在していたことから、式を一般化するレベルの数学力を持っていたと言えるでしょう。
ピタゴラス数のヒントとなる問題
三平方の定理の文章題の中には、ピタゴラス数の求め方につながる問題もありました。
「ピタゴラス数」とは、$~a=3~,~b=4~,~c=5~$のような三平方の定理を満たす整数の組$~(~a~,~b~,~c~)~$のことです。
9章第14問は速さに関する問題
ピタゴラス数につながる問題は、9章第14問にありました。
今二人が同じ所から出発する。
甲の速さは$~7~$、乙の速さは$~3~$である。
乙は東に行き、甲は南に$~10~$歩行ってから北東方向に向かうと乙に会った。
甲・乙の道のりはそれぞれどれだけか。
図で整理すると、以下の通りです。
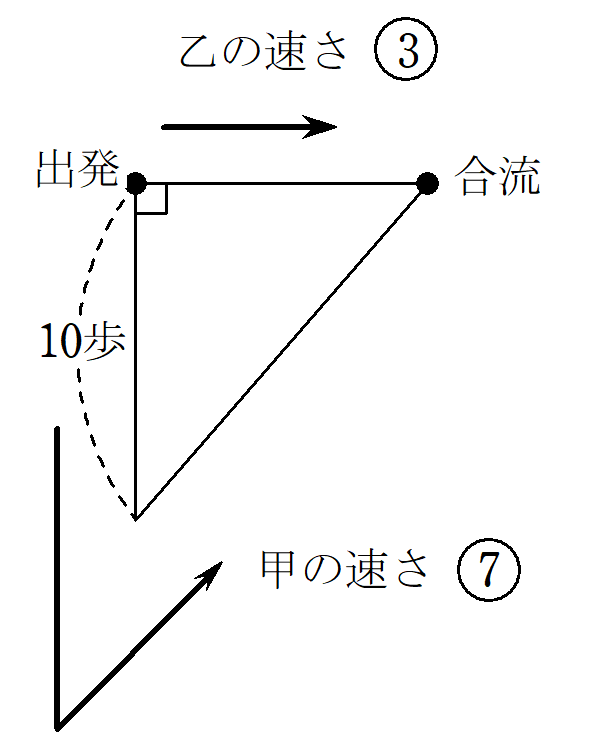
この問題で使われた解法を、現代数学の記法で解説します。
乙の道のりを$~x~$歩、甲の南方向への道のりを$~y~(=10)~$歩、甲の北東方向への道のりを$~z~$歩とする。
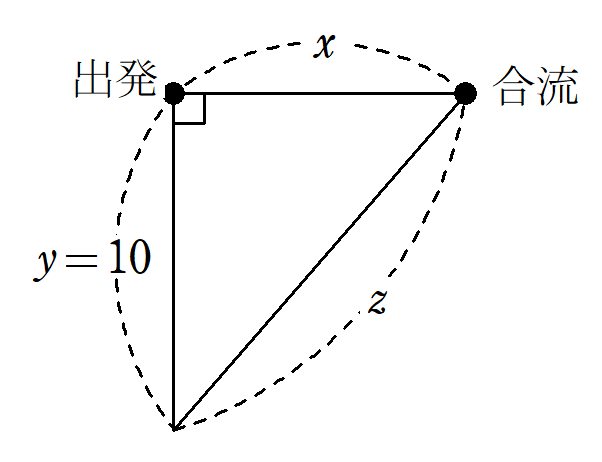
このとき、速さの比から、
y+z=\frac{7}{3}x ~~~\cdots ③であり、三平方の定理から
x^2+y^2=z^2 ~~~\cdots ④
という2本の式ができる。
$~x=3 \cdot 7v~$($~v~$は定数)とすると、$③$は
y+z=7^2v ~~~\cdots ③ ^{\prime}となる。
また、$④$より
\begin{align*}
x^2&=z^2-y^2 \\
x^2&=(z+y)(z-y)
\end{align*}で、$~x=3 \cdot 7v~$と$~③^{\prime}~$を代入すると、
\begin{align*}
3^2 \cdot 7^2 v^2&=7^2v \cdot (z-y) \\
3^2v&=z-y ~~~\cdots ④^{\prime}
\end{align*}となる。
よって、$~③^{\prime}-④^{\prime}~$と$~③^{\prime}+④^{\prime}~$をすることで、
\begin{align*}
y=\frac{7^2-3^2}{2}v~~&,~~z=\frac{7^2+3^2}{2}v \\
\\
y=20v~~&,~~z=29v
\end{align*}が求まり、$~y=10~$より、$~v=\displaystyle \frac{1}{2}~$なので、
x=\frac{21}{2}~~,~~z=\frac{29}{2}と求まる。
すなわち、甲は$~14~$歩半、乙は$~10~$歩半である。
$~z-y~$と$~z+y~$を経由していることが特徴的であり、これがピタゴラス数へとつながる考え方となります。
9章第14問の解法からピタゴラス数の式が得られる
『九章算術』9章第14問の解法において、速さの比率を$~7:3~$から$~a:b~$にすると、$③$は、
y+z=\frac{a}{b}xとなり、$~x=b \cdot a~$とすることで、
y+z=a^2~~,~~z-y=b^2
が出てきます。
したがって、
x=ab~~,~~y=\frac{a^2-b^2}{2}~~,~~z=\frac{a^2+b^2}{2}がピタゴラス数を求める組となります。
ただし、$~a > b~$であり、$~a~$と$~b~$の偶奇が一致している必要があるため注意しましょう。
実際にいくつかピタゴラス数を求めてみると、$~a~,~b~$を奇数にすることで、原始ピタゴラス数($~x~,~y~,~z~$が互いに素)が発見できます。
| $a$ | $b$ | $x$ | $y$ | $z$ |
|---|---|---|---|---|
| $3$ | $1$ | $3$ | $4$ | $5$ |
| $4$ | $2$ | $8$ | $6$ | $10$ |
| $5$ | $1$ | $5$ | $12$ | $13$ |
| $12$ | $8$ | $96$ | $40$ | $104$ |
| $13$ | $7$ | $91$ | $60$ | $109$ |
『九章算術』に登場する直角三角形の三辺の長さはすべて有理数のため、著者はピタゴラス数を求めたうえで作問していたと推測されています。
ちなみに、『九章算術』の約1500年前に、バビロニアでも同じようなピタゴラス数を求める式が作られていました。

まとめ・参考文献
古代中国における三平方の定理について解説しました。
- 古代中国の数学書『九章算術』では、「句股の術」として三平方の定理が知られていた。
- 文章題では、各問題を解くために必要な術(公式)が与えられた。
- ピタゴラス数を作るための公式を知っていた。
基本問題から始まり、難解な文章題の解法まで公式化していた『九章算術』9章「句股」。
著者あるいは当時の中国の高い数学力をうかがい知ることができました。
次の記事では、古代中国の二次方程式について解説します。



葭の問題、今の中3の教科書の応用問題とかに載っていてもおかしくないね。



うん。漢文と数学のコラボ問題ができそうだよ。
参考文献(本の紹介ページにリンクしています)
- 張替俊夫「『九章算術』訳注稿(29)」,< https://core.ac.uk/download/pdf/229489192.pdf>
- 大川俊隆・田村誠「『九章算術』訳注稿(30)」,< https://osu.repo.nii.ac.jp/?action=pages_view_main&active_action=repository_view_main_item_detail&item_id=2016&item_no=1&page_id=13&block_id=21よりダウンロード>
- 『カッツ 数学の歴史』,pp.39-41
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,p.194
- 『数学史 数学5000年の歩み』,pp.135-137
- 『数学の歴史物語』,pp.167-183
- 『ずかん 数字』,pp.70-77

コメント