三平方の定理は別名「ピタゴラスの定理」と呼ばれています。
しかし、定理を発見したのはピタゴラスではなく、彼よりも1000年以上昔のバビロニア人でした。
では、なぜピタゴラスの名が定理についているのか?
この記事では、その歴史的な背景についても触れながら、ピタゴラスが与えた三平方の定理の証明方法について、現役数学教員がわかりやすく解説していきます。
- なぜ三平方の定理がピタゴラスの定理とも呼ばれているか。
- ピタゴラスが考えた、三平方の定理の証明方法
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓

歴史
三平方の定理は別名「ピタゴラスの定理」と呼ばれています。
しかし、実際にこの定理を発見したのはピタゴラス(Pythagoras , B.C.569頃-B.C.500頃)ではなく、彼が生まれる約1000年前からバビロニアで知られていました。
ピタゴラスは若い頃に、エジプトやバビロニアを旅していたため、そのときに学んだとされています。

(出典:The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons)
では、なぜ三平方の定理に彼の名がついているのでしょうか?
それは、ピタゴラスが三平方の定理を初めて証明したからです。
ピタゴラスや タレス(Thales, B.C.625頃-B.C.547頃) をはじめとする古代ギリシャの数学者たちは、「公式や定理がなぜ成り立つか?」という視点で物事を考え、証明するという概念を定例化しました
数式を使わないパズルのような証明方法ですが、公式や性質を証明をしたうえで活用するという姿勢は、現代数学への第一歩となっています。

ピタゴラスの証明方法
バビロニアの人々が当たり前のように使っていた三平方の定理を、ピタゴラスがどのように示したのかを見てみましょう。
一辺が$~a+b~$である正方形において、その内部に一辺がそれぞれ$~a~$,$~b~$となる正方形を作る。
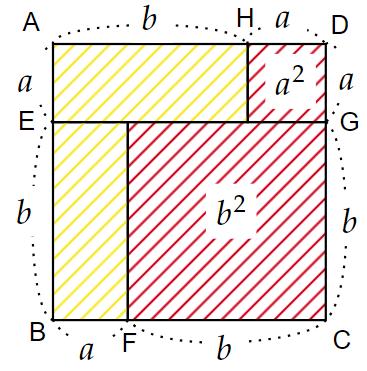
次に、$~EH~,~EF$を結ぶ。
この2つの線分は、辺の長さが$~a~,~b~$である長方形の斜辺となり、長さを$~c~$とおく。
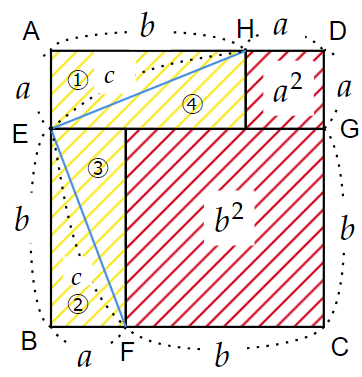
図2の直角三角形③、④を回転移動させることで、図3のようになる。
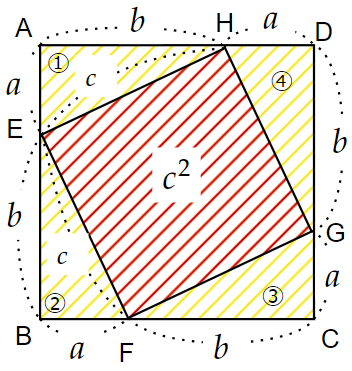
中央の正方形の面積は$~c^2~$となり、これは正方形$~ABCD~$から直角三角形①~④を引いたものである。
したがって、図2の$~a^2~$と$~b^2~$の和と等しくなるので、
c^2=a^2+b^2
が示された。■
回転させて、正方形の中に正方形を作るのがミソです。
数式を使わなければ、小学生以下でも十分理解できる内容だと思います。

なんでバビロニアの人たちは、証明をしなかったんだろう?



バビロニアの人たちは三平方の定理を、建築などで直角を作るための道具としてしか使っていなかったからだよ。
古代ギリシャでは、議論するという行為が流行っていたから、相手を納得させるために証明が必要だったんだ。
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓



コメント