三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。
この記事では、その中でも直角三角形の内接円の性質をフル活用した証明方法について、現役数学教員がわかりやすく解説します。
計算が多い証明方法ではありますが、やっていることは明快。
理解しやすい証明方法の1つなので、この記事を読んで証明のバリュエーションを増やしましょう。
- 内接円を利用した三平方の定理の証明方法
- 三平方の定理の証明を集めた本について
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓

歴史
今回紹介する内接円を利用した証明方法は、1901年の American Mathematical Monthly (アメリカ数学月刊誌)に掲載されていたものです。
しかし、それよりも早くから思いついていたことを主張する人がいました。
1927年に出版された『ピタゴラスの命題』という本の著者であるイライシャ・スコット・ルーミス(Elisha Scott Loomis , 1582-1940)です。

(出典:Finkel, B. F., Public domain, via Wikimedia Commonsより改変)
彼はその著書の中で、古今東西から集めた三平方の定理の証明371個を、分類したうえでまとめています。
ピタゴラスやユークリッドなどの数学者が発見した証明方法から、16歳の女子高生やアメリカの大統領が見つけたものまで、多種多様にまとめてありました。
その中の1つが今回の証明方法で、ルーミスはその本の中で、
この解は著者が1901年12月13日に考案した. Am. Math. Mo.(American Mathematical Monthly ; アメリカ数学月刊誌)vol.Ⅷ , 1901 , p258にも同じような解が載っているが , それを受け取る前に .
E・マオール(2008)『ピタゴラスの定理-4000年の歴史』,p.154 より
と強調されています。
ルーミスが主張しているだけのことなので、どちらが先かを特定するのは困難ですが、ルーミスは三平方の定理の証明の編纂に大きく貢献した人物であることは間違いないでしょう。

ルーミスは三平方の定理の証明ヲタクだったんだね!
内接円を利用した証明方法
証明方法としては、計算量こそ多いものの、考え方としてはわかりやすいです。
直角三角形$~ABC~$に、半径$~r~$の円$~O~$を内接させる。
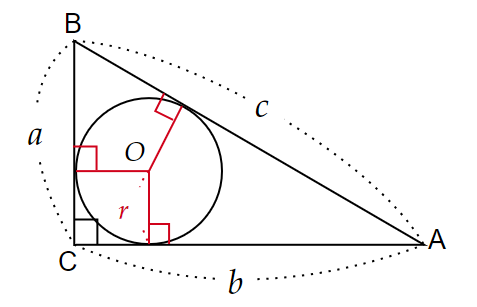

このとき、△ABCの面積$~S~$ は2通りの方法で表せる。
まず、底辺と高さに注目して、
\begin{align*}
S&=b \cdot a \cdot \frac{1}{2} \\
\\
&=\frac{ab}{2}~~~\cdots ①
\end{align*}が成り立つ。
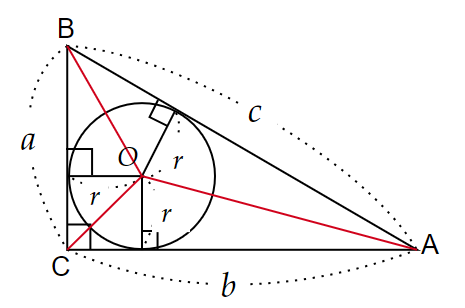

次に、$~AO~,~BO~,~CO~$で$~\triangle ABC~$を3つの三角形に分けることで、
\begin{align*}
S&=\frac{ar}{2}+\frac{br}{2}+\frac{cr}{2} \\
\\
&=\frac{r}{2}(a+b+c)~~~\cdots ②
\end{align*}が成り立つ。
$①$と$②$より、
\begin{align*}
\frac{ab}{2}&=\frac{r}{2}(a+b+c) \\
\\
ab&=r(a+b+c)~~~~\cdots ③
\end{align*}である。
ここで、$~r~$を$~a~,~b~,~c~$を使って表すことを考える。
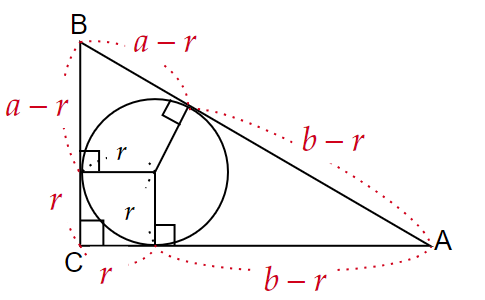

図3で、斜辺$~BA~$に注目すると、
\begin{equation*}
(a-r)+(b-r)=c
\end{equation*}この等式を変形していくことで、
\begin{align*}
-2r&=c-a-b \\
\\
r&=\frac{a+b-c}{2} ~~~~\cdots ④
\end{align*}であり、$④$を$③$に代入することで、
\begin{align*}
ab&=\frac{a+b-c}{2}\cdot (a+b+c) \\
\\
2ab&=(a+b)^2-c^2 \\
\\
2ab&=a^2+2ab+b^2-c^2 \\
\\
c^2&=a^2+b^2
\end{align*}が示された。■
内接円により、面積を2通りの方法で表すことができるため、等式を作ることができます。
そこに$~r~$を$~a~,~b~,~c~$で表した式を代入するだけ!



左下に出てくる正方形がミソだよね。



うん。円と接線の性質をうまく利用しているのがわかるね。
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓



コメント