
数学Ⅰの教科書で必ず出てくる$~\sqrt{2}~$が無理数であることの証明。
証明は背理法で行われますが、矛盾に至るまでにいろいろな方法があるんです!
- $~\sqrt{2}~$の誕生と無理数の証明の歴史
- 教科書に載っている証明方法
- 素因数$~2~$に着目した証明方法
- 正方形の面積を利用した証明方法
Ⅰ √2 の歴史は紀元前から
$~\sqrt{2}~$の存在が知られるようになったのは紀元前6世紀で、ピタゴラス(Pythagoras , B.C.569頃-B.C.500頃)がピタゴラスの定理の証明をし、直角三角形を研究したことがきっかけでした。


(出典:The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons )
$~\angle C=90^{\circ}~$の直角三角形$~ABC~$において、
a^2+b^2=c^2
が成り立つ。
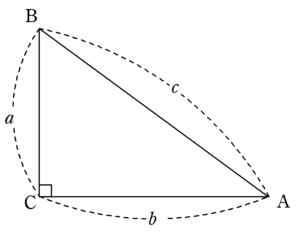

このピタゴラスの定理を、直角二等辺三角形に適用するとある問題が出現します。
それは、$~\sqrt{2}~$は無理数か? です。
当時は通約不能とも言われ、$~\sqrt{2}~$が$~\displaystyle \frac{自然数}{自然数}~$で表せない数ではないかというのが議論の的となっていました。


この問題を解決に導いたのは、ピタゴラス教団の教徒であるヒッパソス(Hippasus , B.C.5世紀中頃)です。


(出典:Boccanera G., Public domain, via Wikimedia Commons)
彼は幾何学的な方法で、$~\sqrt{2}~$が無理数であることを証明したと言われています。
しかし、万物の根源を数に求めるピタゴラス教団の信念に背く発見であり、それを口外したヒッパソスは他の教団員に溺死させられました。
このように、紀元前から$~\sqrt{2}~$が無理数であることは言及されてきましたが、実際どのような方法で証明すればよいのでしょうか?
※$~\sqrt{~~}~$の記号が実際に使われたのは、16~17世紀頃です。
Ⅱ 証明の共通点は背理法
無理数であることを証明するにあたって、どの証明方法でも共通しているのは背理法を用いるということです。
背理法の手順を確認しておきましょう。
- 結論の否定を仮定する。
- その仮定から計算や論理を進める。
- 進める中で矛盾を生じさせる。
矛盾が生じることで、結論の否定が間違っていた → 結論は正しい という主張ができます。
この考え方は、数学だけでなく日常生活でも2つの選択肢から1つを選ぶときに使えます。
「健康的な生活には睡眠が必要である」という主張をしたいとき
- 「睡眠が不要である」と仮定する。
- 睡眠をとらないと、寝不足で頭痛が起こる。
- 頭痛が起こるというのは、健康的な生活に矛盾。よって、睡眠は必要である。
「頭痛が起こる」とか、それが「健康的でない」というのは、個人的な経験や考えに基づくため、すべての人にこの証明があてはまるとは一概に言えません。
ただ、数学であれば、1つ1つの用語がきちんと定義されたうえで論理を進めるため、誰がどう見ても矛盾があると言えるような証明を行うことができます。
それにしても、結論が間違っていることを前提に話を進めて、矛盾を生じさせるなんて、個人的にはひねくれた証明方法のように思えます。
Ⅲ 「互いに素」を利用した証明方法
では、実際に背理法を使って、$~\sqrt{2}~$が無理数であることを証明してみましょう。
1つ目の証明方法は、数学Ⅰの教科書によく載っている、互いに素(最大公約数が$~1~$)であることを利用した証明方法です。
この方法を用いるにあたり、次の補題が必要となります。
$~n~$を整数とする。このとき、$~n^2~$が偶数ならば、$~n~$は偶数である。
$~16~$や$~100$のように、平方数が偶数ならば、その正の平方根$~4~$や$~10~$も偶数という当たり前のような命題です。
証明は、対偶を使えばすぐにできます。
この命題の対偶「$~n~$ならば、$~n^2~$は奇数である。」を証明する。
奇数 $~n~$は、整数$~k~$を用いて$~n=2k+1~$と表されるので、
\begin{align*}
n^2&=(2k+1)^2 \\
&=4k^2+4k+1 \\
&=2(2k^2+2k)+1 \\
\end{align*}であり、$~2k^2+2k~$は整数なので、$~n^2~$は奇数となる。
よって、対偶が示されたので、元の命題も示された。■
では、この補題を使って、 $~\sqrt{2}~$が無理数であることの証明をしてみましょう。
背理法で示す。
$~\sqrt{2}~$は無理数ではない、つまり有理数であると仮定すると、$~\sqrt{2}~$は互いに素な2つの自然数 $~a~,~b~$を用いて、
\sqrt{2}=\frac{a}{b}と表せる。
この式を変形していくと、
\begin{align*}
a&=\sqrt{2}b \\
\\
a^2&=2b^2 ~~~~\cdots①
\end{align*}であるため、$~a^2~$は偶数であることがわかる。
さらに、補題1より、$~a~$も偶数となる。$~~~\cdots ②$
$②$より、$~c~$を自然数とすると、
a=2c~~~~\cdots ③
であるため、$③$を$①$に代入すると、
\begin{align*}
(2c)^2&=2b^2 \\
4c^2&=2b^2 \\
2c^2&=b^2
\end{align*}が成り立ち、$~b^2~$は偶数であることがわかる。
さらに、補題1より、$~b~$も偶数となる。$~~~\cdots ④$
$②~,~④$より、$~a~,~b~$は共に偶数であることが示されたが、これは$~a~,~b~$ が互いに素であることに矛盾する。
よって、$~\sqrt{2}~$が無理数であることが示された。■
$~a~,~b~$が互いに素なので、最大公約数が$~1~$となるはずが、$~a~,~b~$が共に偶数だと、最大公約数は少なくとも$~2~$であることがわかり、矛盾となります。
$~\sqrt{2}~$を$~\displaystyle \frac{a}{b}~$という既約分数で表してあげるというのが、矛盾を生じさせるために必要なので、「互いに素」であるということを書き忘れないようにしましょう。
Ⅳ 素因数 2 の個数を利用した証明方法
素因数$~2~$が両辺に何個ずつあるかに着目することで、矛盾を見つける方法です。
こちらも、予め知っておくべき補題から解説します。
$~n~$を整数とする。このとき、$~n^2~$が持つ素因数$~2~$は偶数個である。
いくつかの平方数を例に考えてみましょう。
- $~4^2=16=2^4~$
- $~5^2=25=2^0\cdot 5^2~$
- $~6^2=36=2^2\cdot 3^2~$
- $~8^2=64=2^6~$
どの平方数も、素因数分解したときの素因数$~2~$の指数は偶数になっています。
証明は数学Ⅰで登場する、余りで場合分けをする手法です。
$~n~$を$~2~$で割ったときの余りで場合分けをする。
(1) $~n~$が奇数のとき
整数$~k~$を用いて$~n=2k+1~$と表せる。このとき、
\begin{align*}
n^2&=(2k+1)^2 \\
&=4k^2+4k+1 \\
\end{align*}となるため、素因数$~2~$は0個(偶数個)である。
(2) $~n~$が偶数のとき
$~n~$を素因数分解すると、次のように表せる。
n=2^m \cdot a ~~~~~~~~~(m~は自然数~,~a~は奇数)
このとき、
\begin{align*}
n^2&=(2^m \cdot a)^2 \\
&=2^{2m} \cdot a^2
\end{align*}であり、$~2^{2m}~$には素因数$~2~$が偶数個あり、$~a^2~$ には (1) より素因数$~2~$が0個であるため、 $~n^2~$ が持つ素因数$~2~$は偶数個である。
(1)、(2)より題意は示された。 ■
若干、この補題の証明が難しいですが、これを乗り越えれば本題の証明は簡単です。
背理法で示す。
$~\sqrt{2}~$は無理数ではない、つまり有理数であると仮定すると、$~\sqrt{2}~$は互いに素な2つの自然数 $~a~,~b~$を用いて、
\sqrt{2}=\frac{a}{b}と表せる。
この式を変形していくと、
\begin{align*}
a&=\sqrt{2}b \\
\\
a^2&=2b^2 ~~~~\cdots⑤
\end{align*}となる。
補題2より、$⑤$の左辺の$~a^2~$が持つ素因数$~2~$は偶数個である。
同様に、$~b^2~$が持つ素因数$~2~$は偶数個であるが、そこに$~2~$を1つかけているため、 $①$の右辺の $~2b^2~$が持つ素因数$~2~$は奇数個となる。
以上から、素因数$~2~$の個数が両辺で異なることに矛盾。
よって、$~\sqrt{2}~$が無理数であることが示された。■
右辺の$~2~$がこんな形で役に立つなんて想定外ですよね。
Ⅴ 正方形の面積を利用した証明方法
最後は、ピタゴラス教団が好きそうな、幾何的な証明。
補題は必要ありません。
背理法で示す。
$~\sqrt{2}~$は無理数ではない、つまり有理数であると仮定すると、$~\sqrt{2}~$は互いに素な2つの自然数 $~a~,~b~$を用いて、
\sqrt{2}=\frac{a}{b}と表せる。
この式を変形していくと、
\begin{align*}
a&=\sqrt{2}b \\
\\
a^2&=2b^2 ~~~~\cdots⑥
\end{align*}となる。
ここで、$~\sqrt{2}~$は、$~1 < \sqrt{2} < 2~$であるため、$~a~,~b~$に関して、$~\displaystyle 1 < \frac{a}{b}~$から、次の3つの条件がわかる。
\begin{align*}
b &< a \cdots ⑦ \\
0 &< a-b \cdots ⑧ \\
2b-a &< a \cdots ⑨
\end{align*}また、$~\displaystyle \frac{a}{b} < 2~$から、次の3つの条件がわかる。
\begin{align*}
0 &< 2b-a \cdots ⑩ \\
a-b &< b \cdots ⑪
\end{align*}$⑦$より、1辺$~a~$の正方形に、1辺$~b~$の正方形2つを入れた図4を考える。
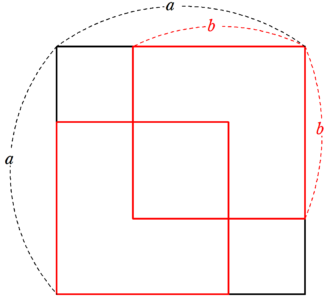

左上と右下の正方形の1辺の長さは$~a-b~$、中央の正方形の1辺の長さは$~a-(a-b)-(a-b)=2b-a~$である。
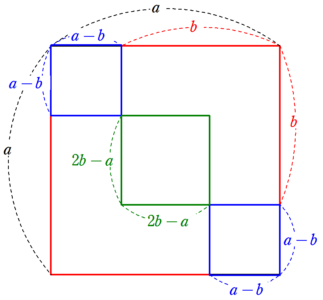

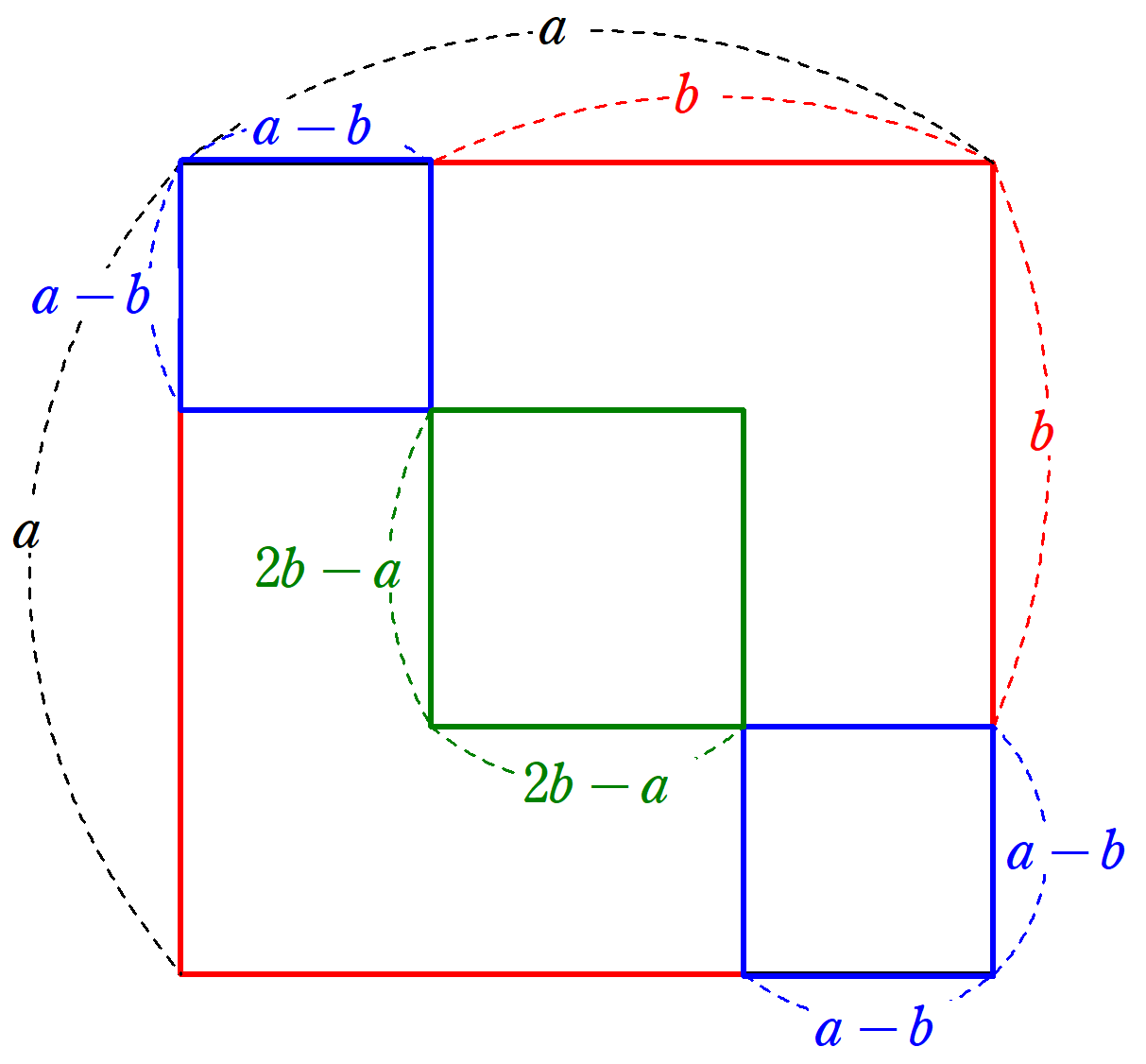
ここで、1辺$~a~$の正方形は、1辺$~b~$の正方形2つ分から、1辺$~2b^a~$の正方形を引き、1辺$~a-b~$の正方形を足すことで求まるため、
b^2+b^2-(2b-a)^2+2(a-b)^2=a^2
が成り立つ。
この等式に$⑥$を代入すれば、
\begin{align*}
2b^2-(2b-a)^2+2(a-b)^2&=2b^2 \\
2(a-b)^2&=(2b-a)^2 \\
2&=\frac{(2b-a)^2}{(a-b)^2} \\
\end{align*}であり、$⑧$と$⑩$に注意して、両辺正の平方根をとると、
\sqrt{2}=\frac{2b-a}{b-a}が求まる。
しかし、$⑨$と$⑪$より、$~\displaystyle \frac{2b-a}{b-a}~$は$~\displaystyle \frac{a}{b}~$を約分した(分母・分子の数が小さくなった)ものであり、 $~a~,~b~$が互いに素であることに矛盾。
よって、$~\sqrt{2}~$が無理数であることが示された。■
$~a~,~b~$が互いに素であるということは、 $~\sqrt{2}=\displaystyle \frac{a}{b}~$が既約分数となるため、これ以上約分することはできません。
しかし、$~\sqrt{2}~$を有理数と仮定して、正方形の面積を考えてあげると、この$~\sqrt{2}~$が $~\displaystyle \frac{a}{b}~$の分母と分子の数をより小さくした分数で表せることになるため、既約分数であることに矛盾するというトリッキーな方法でした。
どの証明方法も同じ始まり方をしているのに、矛盾の生じさせ方が違う点がおもしろいですね。



三平方の定理ほどではないけど、いろいろな証明方法があって面白いね。



さすが三平方の定理とほぼ同時期に出てきた、歴史のある問題って感じです。
参考文献
- 結城浩(2008)『数学ガール/フェルマーの最終定理』 , pp.102-105 , SB Creative.

コメント
コメント一覧 (4件)
素因数 2 の個数を利用した証明方法の2個目について、自分の持っている参考書に「aとbが互いに素である必要はない」と明記されてあるのですが、この証明方法においてaとbが互いに素であることを書いても書かなくてもどちらでもよいのでしょうか。
ropi様
コメントありがとうございます。
素因数$~2~$の個数を利用した証明方法に関しては、矛盾の材料が「互いに素」ではないため、明記しなくても証明自体は成立します。
ただ、$~\displaystyle \frac{a}{b}~$を既約分数としたほうが、表現としてはわかりやすいので、「互いに素」を入れることを個人的には推奨します。
どちらの証明も「√2が有理数であることが示された。」と書いてあります。無理数ですよね?訂正お願いします。
ご指摘ありがとうございます。訂正いたしました。
結論を間違えるという、元も子もないことをしてしまいましたm(_ _)m
今後ともどうぞよろしくお願いいたします。