√ の由来

平方根で出てくる根号√（ルート）が、なぜこのような形になったのかを解説します。

Ⅰ　平方根の必要性

　まずは、平方根という考え方が必要となった背景に迫ってみましょう。

　平方根の起源は、紀元前６世紀頃の ピタゴラス（Pythacoras , B.C.569頃-B.C.500頃）にまで遡ります。
　ピタゴラスといえば、ご存知の通り、次の定理が有名です。

三平方の定理（ピタゴラスの定理）

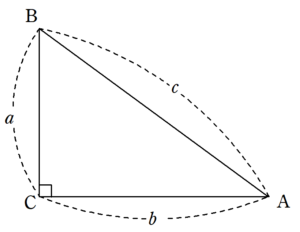
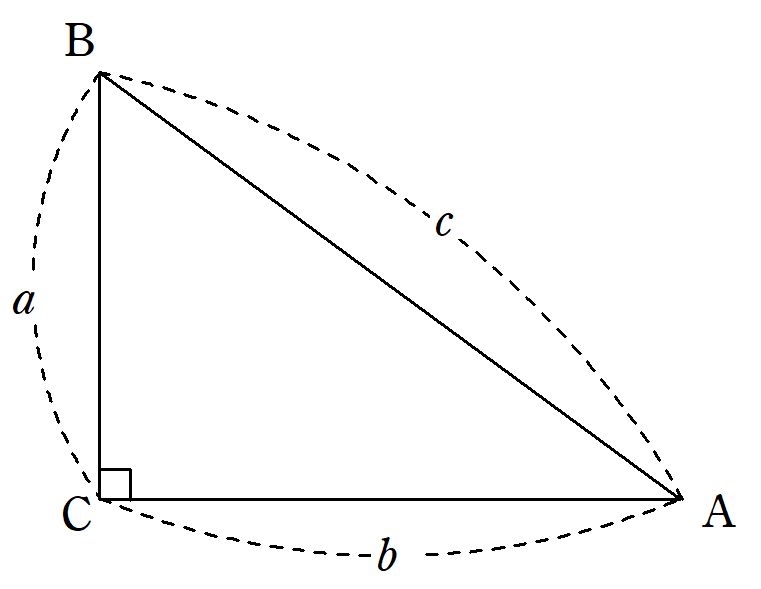
　図１のような直角三角形で、次の等式が成り立つ。

\begin{equation*}
c^2=a^2+b^2
\end{equation*}

　この定理を、$~a=1,b=1~$の直角二等辺三角形に適用すると、

\begin{align*}
c^2&=1^2+1^2 \\
c^2&=2 \\
\end{align*}

であり、斜辺$~c~$は２乗したら$~2~$になる数、すなわち$~\sqrt{2}~$という数が必要となります。
 
　しかし、定理を示したピタゴラスは

ピタゴラス

万物は整数と分数で表せる！

（出典：The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons）

という「万物は数である」という信条を持っていたため、 $~\sqrt{2}~$ という無理数を認めず、平方根という概念や記号など考えもしませんでした。

　また、紀元前４世紀頃のユークリッドも $~\sqrt{2}~$ が無理数であることの証明 はしたものの、平方根を表す記号までは使っていませんでした。

　根号（√）の誕生は、そこから1000年以上待つことになります。

Ⅱ　様々な表記法の誕生

　中世ヨーロッパでは、いろいろな数学者たちが$~\sqrt{\quad}~$を様々な方法で表記しています。

Ⅱー①　レオナルド・フィボナッチ

　フィボナッチ数列で有名なレオナルド・フィボナッチ（Leonardo Fibonacci , 1180頃-1250頃）は、1202年に著書『算盤の書』の中で、$~\sqrt{2}~$のことを、radix de$~2~$と書いています。

　ちなみに、”radix “という単語はラテン語で「根」を表します。

Ⅱー②　レギオモンタヌスとカルダノ

　15世紀に『三角法』を書いたドイツの数学者レギオモンタヌス（Regiomontanus , 1436-1476）や、16世紀に ３次方程式の解の公式 を導いたジェロラモ・カルダノ（Girolamo Cardano , 1501-1576）は、$~\sqrt{2}~$のことを、℞$~2~$と書いています。

　この「℞」という記号は、ラテン語で「根」を表す”Radix “の頭文字”R”と語尾の”x”を組み合わせたものです。
 
　また、$~\sqrt[3]{8}~$などの３乗根は、 ℞.cube.de.$~8~$や cu.℞$~8~$というように表されています。（”cube “は「立方」を表す英語）

Ⅱー③　ラムスとヘンリー

　１６世紀のフランスの論理学者ピエール・ラムスや、1624年に『対数算術』を出版したイギリスのブリッグス・ヘンリー（Briggs Henry , 1561-1630）は、$~\ell~$を使って、$~\ell 2~$と表しています。
 
　これは、ラテン語の”latus “、「一辺」を表す単語であり、正方形の面積に対して、１辺の長さが平方根にあたることから考えられたものとされています。
 
　ちなみに、３乗根についても$~\ell_3 8~$と表しています。

Ⅱー④　ルドルフ

　ついに今の$~\sqrt{\quad}~$の原形となるものが誕生します。

　それを生み出したのは、ドイツの数学者クリストフ・ルドルフ（Christoff Rudolff , 1500-1545頃)です。
　※円周率のルドルフ・ファンケーレンとは別人

　クリストフ・ルドルフは1525年の著書『未知数』の中で、√ $~2~$と表しています。
 
　ルドルフがそれ以前に書いていた本では、$~r 2~$と記載していたため、”radix “すなわち”root “の頭文字”r “を殴り書きしていくうちに、変形したものが$~\sqrt{\quad}~$と言われています。

　この点を見ると、”minus “の頭文字”m”から$~-~$が生まれたのと同じですね。

あわせて読みたい

非公開: ＋や－の由来 よく使う数学記号の１つである＋や－の由来を調べてみました。 Ⅰ　１２世紀の西欧にて Ⅱ　ヨハン・ウィッドマンと $~+,-~$ の誕生 Ⅰ　１２世紀の西欧にて アル・フワー…

　ちなみに、ルドルフは３乗根や４乗根を以下のように表しています。

　見分けづらいですね。

Ⅲ　現在の形へ

　ルドルフの √ をきっかけに、あらゆる数学者が今の形に近い累乗根の表記を使っています。

Ⅲー①　オートレッド

　イギリスの数学者ウィリアム・オートレッド（William Oughtred , 1574-1660）が1631年に書いた『数学の鍵』の中で、立方根を√$_c 8~$、６乗根を√$_{cc} 64~$と表しました。平方根では√$_r2~$という記号を使い、見た瞬間に何乗根なのかをわかるようにしています。

Ⅲー②　デカルト

　同じく１７世紀前半、フランスのルネ・デカルト（Rene Descartes , 1596-1650）は、数式を書く中で、根号の中に入る式がどこからどこまでなのかを明確にするために、$~\bar{2}~$と書いていました。

　確かに$~\sqrt{a+b}~$が √$a+b~$と書かれていたら、$~\sqrt{a}+b~$と間違いやすいです。

　そして、デカルトはルドルフの記号 $~\sqrt{\quad}~$ と合わせ、$~\sqrt{2}~$という今の形が生まれました。
 
　しかし、３乗根についてはオートレッドと同様、$~\sqrt{_c8}~$というような表記をしています。

Ⅲー③　ニュートン

　１７世紀後半、イギリスのアイザック・ニュートン（Isaac Newton , 1642-1727）は、立方根と４乗根について、$~\sqrt[3]{} 8,\sqrt[4]{}16~$という、今と似たような形で書いています。
（やがて１８世紀に、デカルトの表記と合わせ、$~\sqrt[3]{8},\sqrt[4]{16}~$に統一されていきます）

　ただ、後にニュートンは$~\sqrt{a}~$を$~\displaystyle a^{\frac{1}{2}}~$、$~\displaystyle \frac{1}{a}~$を$~\displaystyle a^{-1}~$と書いていて、代数計算上便利な指数表記へと変わっていきました。
 
　しかしながら、平方根や立方根はその使用頻度から $~\sqrt{2}~$ や $~\sqrt[3]{8}~$ という記号が今も使われています。

凄まじき数学者のリレー・・・。

他の記号もそうだけど、便利に表すために改良が繰り返されていったのがよくわかるね。