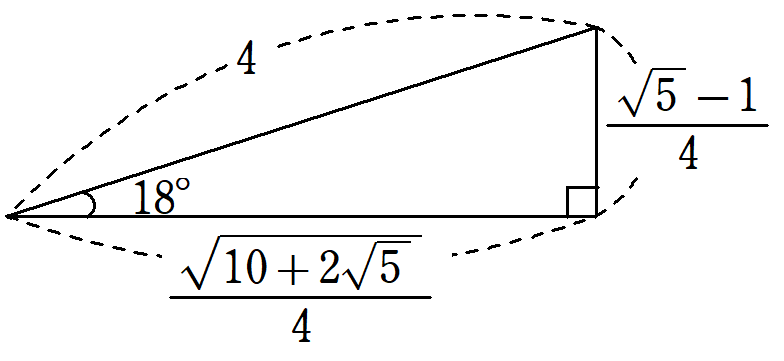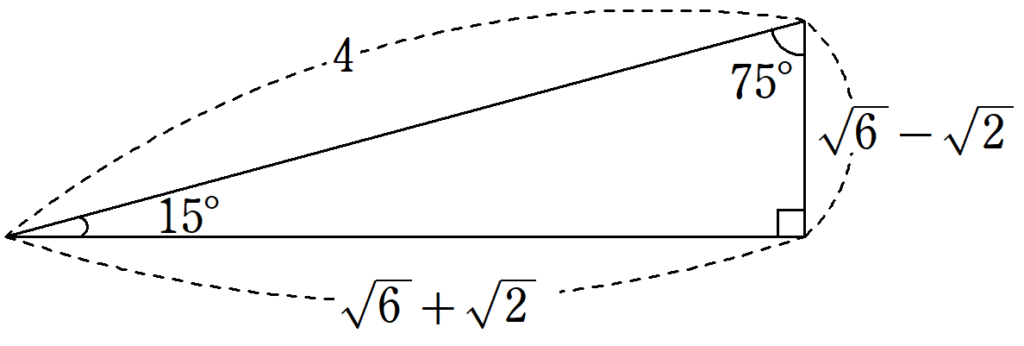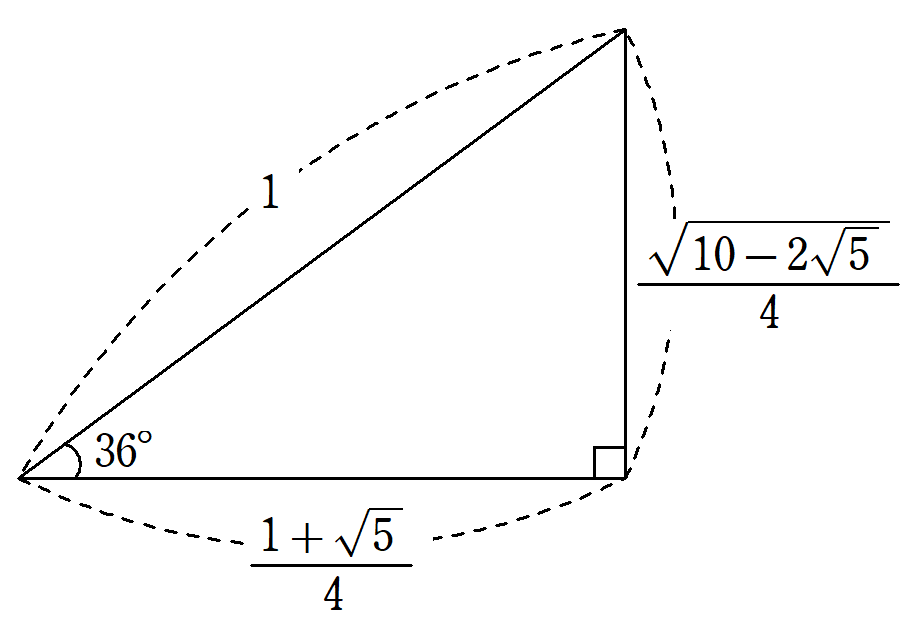三角比・三角関数– tag –
-

【数学史2-6】リンド・パピルスの有名問題を解説!方程式は仮置法で解ける!
古代エジプトの数学を知る上で、欠かせない資料が『リンド・パピルス』。「アハ問題」と呼ばれる方程式の問題やピラミッドの勾配の問題、等比数列の和の問題など、様々な分野の問題を扱っています。この記事では、その中でも有名な3つの問題を解説。今の数学でも使われたり、英語圏の童謡になっていたりと、現代にあらゆる形で残っています。 -

【まとめ】三角比の値~マイナーな角度の三角比まで表形式で紹介~
0°から90°までの三角比の値。数学Ⅰで学ぶのは0°、30°、45°、60°、90°の5つです。しかし、これらの角以外にも小数を使わずに正確な値を出せる角度があります。それらの値について、表形式でまとめました。リンク先の個別ページでは、値の出し方まで解説しています。 -

【数学史3-7】ピタゴラスの定理はバビロニアが最初?粘土板の表に隠された秘密とは?
紀元前1800年頃のバビロニアでは、すでに三平方の定理が知られていました。ピタゴラスの誕生が紀元前6世紀なので、彼の1000年以上前に研究されていたことになります。その根拠となる粘土板や、そこに書かれていたピタゴラス数の求め方について、この記事では解説します。 -

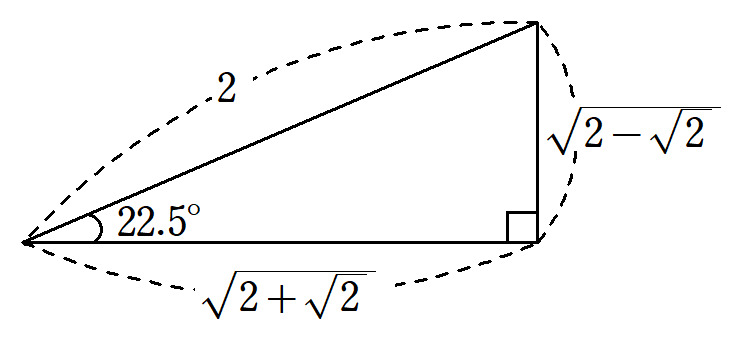
22.5°の三角比 ~半角の公式を使わずに、sin22.5°, cos22.5°, tan22.5°を求める方法を解説!~
22.5°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が2通りの方法で解説。この記事を読むことで、数学Ⅱの半角の公式を使わずに、数学Ⅰまでの知識で値を求める方法がわかります。 -

18°の三角比 ~黄金三角形からsin18°, cos18°, tan18°の値の求める方法を解説~
18°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。この記事を読むことで、36°の三角比から半角の公式を用いる方法、黄金三角形から直接cos18°を求める方法の2種類について理解することができます。 -

複素数の三角関数
$~\sin{x}~$が、$~\sin{z}~$だったら? 複素数の三角関数の定義や成り立つ公式、実数のときとの違いについて解説します。 -

15°の三角比~sin15°, cos15°, tan15°の値の求め方を3種類解説! 加法定理、半角の公式、直角三角形で導ける!~
15°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。この記事を読むことで、三角関数の加法定理や半角の公式を使う方法だけでなく、幾何的に求める方法まで理解することができます。 -

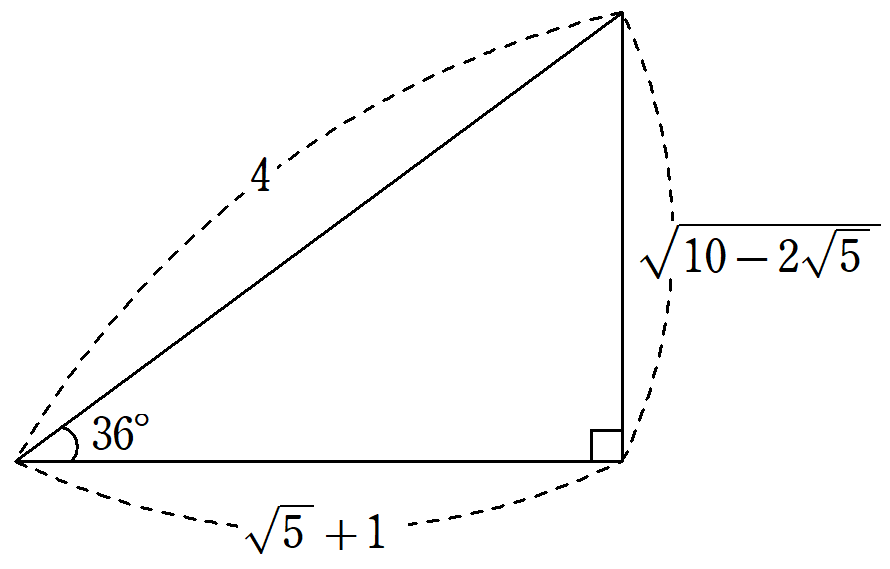
36°の三角比 ~黄金比からsin36°, cos36°, tan36°の値を求める方法を解説!~
36°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。値を求める鍵は、古来から人間を魅了してきた黄金比です。この記事を読むことで、黄金比の計算が36°の三角比にとう繋がっているかがわかります。 -

私学適性(数学)平成30年度解説 大問5
東京都私学教員適性検査の過去問(平成30年度)の答えを解説付きで載せています。問題集の解答例で、解法を調べたい際にご活用ください。大問1大問2大問3大問4大...
1